라그랑주 승수
이 방법은 제약조건(Contraint)이 있을 때, 최적화 문제를 푸는 방법이다.
제약조건이 없는 상황에서의 최적화 문제
제약조건이 없는 상황에서의 최적화 문제를 푸는 경우엔 간단히 미분을 통해서 해결할 수 있다.
만약 우리가 함수 f(x) 의 최솟값을 찾는 최적화 문제를 풀고 있다고 생각해보자.
그렇다면 우리는 f'(x) = 0 을 이용하여 기울기가 0인 지점을 찾게 된다.
f'(x) = 0 인 지점은 극소점 뿐만 아니라 극대점일 수도 있다.
다만 우리가 이렇게 f'(x)를 찾는 이유는 이게 최솟값의 필요조건이기 때문이다.
우리는 이렇게 간단히 후보를 얻은 후에 다른 조건들을 이용해 최솟값을 찾는다.
제약조건이 있는 상황에서의 최적화 문제
제약이 있다고 하면, 단순히 미분을 통해서 해결할 수는 없다.
예를 들어, 우리가 f(x)의 최솟값을 찾는데 이때의 x 값이 g(x) = 0을 만족해야 하는 조건이 있는 상황을 생각해보자.
그렇다면 우리는 f'(x) = 0을 만족시키는 점 x가 g(x) = 0을 만족시킨다는 보장이 없기에 단순히 미분을 통하여 해결할 수 없다.
우리가 미분을 통해 최솟값을 찾는 이유를 좀 더 생각해보자.
최솟값을 직접 구하기 이전에 최솟값의 필요조건인 f'(x) = 0인 지점을 찾는 작업을 수행한다.
라그랑주 승수도 이와 동일한 논리로 필요조건을 먼저 찾는다.
그렇다면 f(x)의 최솟값을 찾는데 이때의 x 값이 g(x) = 0을 만족해야 하는 조건이 있는 상황을 해결하기 위해서는 어떤 필요조건이 있을까?
라그랑주 승수의 필요조건
해당 조건을 만족하는 x에 대해 다음이 필요조건이 된다.
- 가 존재
조건에 대해서 생각해보면 1번 조건은 문제 상황의 제약조건인 식이므로 당연하다.
2번 조건은 함수 f의 그레디언트와 함수 g의 그레디언트가 평행해야 한다는 의미이다.
그레디언트가 왜 평행해야 할까?
이를 이해하기 위해서는 방향 도함수 개념과 그레디언트(기울기 벡터)의 개념을 알아야 한다.
방향도함수 (스칼라)
방향도함수란 단위벡터 u 방향으로의 f(x,y) 의 변화율(스칼라)을 의미한다.
만약 단위벡터 u가 x축에 평행한 방향이라면 x에 대한 편미분, 즉 x방향으로의 f의 변화율이다.
그레디언트 (, 기울기 벡터)
기울기 벡터는 각 성분의 편미분으로 정의된다.
만약 f가 x,y에 대한 함수라면 다음과 같다.
그레디언트는 해당 점에서 가장 가파르게 올라가는 방향을 가리키게 되는데, 이는 방향도함수 개념으로 설명할 수 있다.
위에서도 나왔지만 방향도함수는 단위벡터 u 방향으로 움직였을 때의 f(x,y)의 변화율을 의미한다.
식을 써보면 다음과 같다.
cos의 범위는 -1 ~ 1이므로 방향벡터와 그레디언트가 평행할 때 변화율이 최대가 된다.
참고로 이때 f의 그레디언트와 수직한 방향으로 움직인다면 cos = 0이 되어, 방향도함수가 0이 된다.
방향도함수가 0이 된다는 의미는 해당 방향으로 가도 f(x,y)의 값이 변화하지 않음을 의미한다.
라그랑주 승수
다시 라그랑주 승수의 필요조건으로 돌아와서, 조건 2를 살펴보자.
- 을 만족하는 가 존재
2번 조건은 와 가 평행해야 한다는 뜻이다.
만약 와 가 평행하지 않다면 어떤 현상이 일어날까?
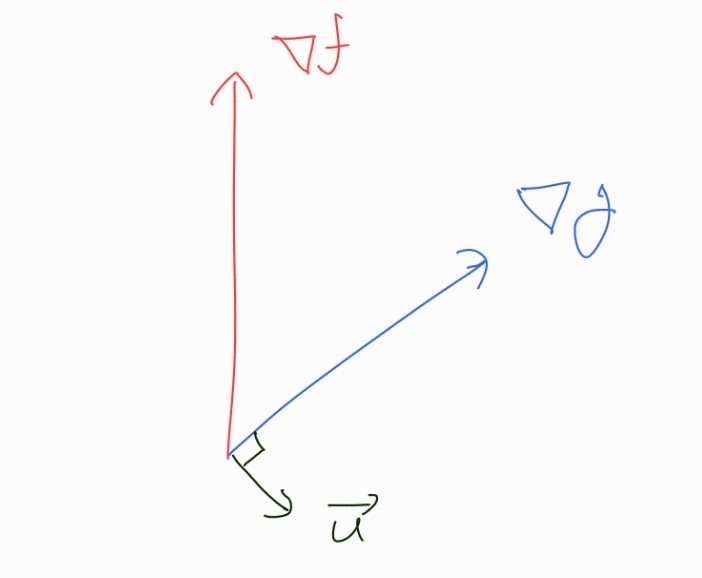
만약 우리가 g(x) = 0을 만족하면서 f(x)를 최소로 만드는 점 x를 찾았다고 해보자.
위 그림에서 와 수직인 u 방향으로 점 x를 이동시킨다고 했을 때, 수직이므로 방향도함수 값이 0이 되고, g(x) = 0이 유지된다.
하지만 와의 각은 90도 이상이므로 u 방향으로 움직인다면 f(x)의 값은 감소한다.
즉, 최소로 만드는 점이라는 가정에 모순이 되는 것이다.
따라서 2번 조건인 와 가 평행은 x가 만족해야 하는 필요조건이 된다.
라그랑주 승수 문제 푸는 방법
위에서 보았듯 라그랑주 승수 문제는 두 가지 조건을 만족해야 한다.
이를 이용해서 우리는 라그랑주 승수 문제를 해결할 수 있다.
f(x)를 최소화하는 문제에서 h(x) = 0인 제약조건이 있으면 다음과 같이 접근하면 된다.
L 함수를 다음과 같이 정의한 후,
조건 1,2을 이용해서 다음 식 두 가지를 얻고 연립한다.