이번 포스트에서는 Gram-Schmidt Process에 대해 알아보겠습니다.
1) The Gram-Schmidt Process
이전 포스트에서 orthogonal projection에 대해서 알아보았습니다. { u 1 , . . . , u p } \{\boldsymbol{u_1}, ..., \boldsymbol{u_p}\} { u 1 , . . . , u p } W W W y \boldsymbol{y} y W W W R n \mathbb R^n R n The Gram-Schmidt process는 subspace의 orthogonal basis를 찾아주는 알고리즘입니다.
다음의 예시를 통해 어떻게 orthogonal basis를 찾을 수 있는지 확인해봅시다.
example
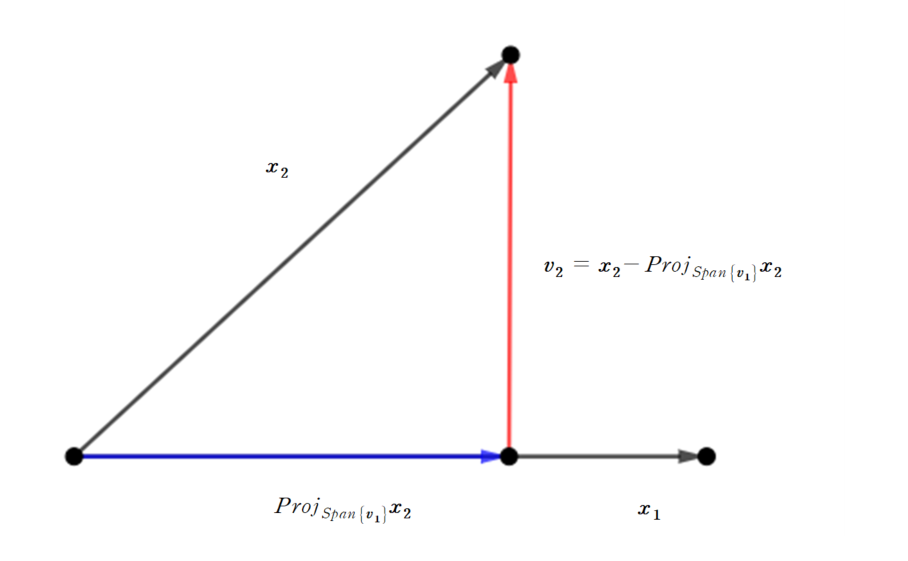
W = S p a n { x 1 , x 2 } , x 1 = [ 3 6 0 ] , x 2 = [ 1 2 2 ] W = Span\{\boldsymbol{x_1}, \boldsymbol{x_2}\}, \ \ \boldsymbol{x_1}=\begin{bmatrix}3 \\ 6 \\ 0\end{bmatrix}, \ \ \boldsymbol{x_2}=\begin{bmatrix} 1 \\ 2 \\ 2 \end{bmatrix} W = S p a n { x 1 , x 2 } , x 1 = ⎣ ⎢ ⎡ 3 6 0 ⎦ ⎥ ⎤ , x 2 = ⎣ ⎢ ⎡ 1 2 2 ⎦ ⎥ ⎤ x 1 , x 2 \boldsymbol{x_1}, \boldsymbol{x_2} x 1 , x 2 { x 1 , x 2 } \{\boldsymbol{x_1}, \boldsymbol{x_2}\} { x 1 , x 2 } W W W
v 1 = x 1 v 2 = x 2 − p r o j S p a n { v 1 } x 2 \boldsymbol{v_1} = \boldsymbol{x_1} \\ \boldsymbol{v_2} = \boldsymbol{x_2} - proj_{Span{\boldsymbol\{v_1\}}}\boldsymbol{x_2} v 1 = x 1 v 2 = x 2 − p r o j S p a n { v 1 } x 2 으로 설정해봅시다. 위와 같이 설정을 하면
v 1 ⋅ v 2 = 0 \boldsymbol{v_1} \cdot \boldsymbol{v_2} =0 v 1 ⋅ v 2 = 0 을 만족합니다. 또한, v 1 ∈ W \boldsymbol{v_1} \in W v 1 ∈ W S p a n { v 1 } ⊂ W Span\{\boldsymbol{v_1}\} \subset W S p a n { v 1 } ⊂ W p r o j S p a n { v 1 } x 2 ∈ W proj_{Span\{\boldsymbol{v_1}\}}\boldsymbol{x_2} \in W p r o j S p a n { v 1 } x 2 ∈ W
v 2 ∈ W \boldsymbol{v_2} \in W v 2 ∈ W 입니다. 실제로 값을 구해보면
p r o j S p a n { v 1 } x 2 = v 1 ⋅ x 2 v 1 ⋅ v 1 v 1 = 15 45 v 1 = [ 1 2 0 ] proj_{Span\{\boldsymbol{v_1}\}}\boldsymbol{x_2} = \frac{\boldsymbol{v_1}\cdot\boldsymbol{x_2}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1 } = \frac{15}{45}\boldsymbol{v_1 } = \begin{bmatrix}1 \\ 2 \\ 0 \end{bmatrix} p r o j S p a n { v 1 } x 2 = v 1 ⋅ v 1 v 1 ⋅ x 2 v 1 = 4 5 1 5 v 1 = ⎣ ⎢ ⎡ 1 2 0 ⎦ ⎥ ⎤ 가 되어
v 2 = [ 0 0 2 ] \boldsymbol{v_2} = \begin{bmatrix} 0 \\ 0 \\ 2\end{bmatrix} v 2 = ⎣ ⎢ ⎡ 0 0 2 ⎦ ⎥ ⎤ 가 되어
v 1 ⋅ v 2 = 0 \boldsymbol{v_1} \cdot \boldsymbol{v_2}=0 v 1 ⋅ v 2 = 0 을 만족합니다. 따라서
{ v 1 , v 2 } \{\boldsymbol{v_1}, \boldsymbol{v_2}\} { v 1 , v 2 } 는 W W W
기본에 알고 있는 x 1 , x 2 \boldsymbol{x_1}, \boldsymbol{x_2} x 1 , x 2 v 1 , v 2 \boldsymbol{v_1}, \boldsymbol{v_2} v 1 , v 2 v 1 \boldsymbol{v_1} v 1 그 다음 새로운 벡터 v 2 \boldsymbol{v_2} v 2 x 2 \boldsymbol{x_2} x 2 S p a n { v 1 } Span\{\boldsymbol{v_1}\} S p a n { v 1 } 이렇게 만들어진 두 벡터 v 1 , v 2 \boldsymbol{v_1}, \boldsymbol{v_2} v 1 , v 2
Theorem : The Gram-Schmidt Process
Given a basis { x 1 , . . . , x p } \{\boldsymbol{x_1}, ..., \boldsymbol{x_p}\} { x 1 , . . . , x p } W W W R n \mathbb R^n R n
v 1 = x 1 v 2 = x 2 − v 1 ⋅ x 2 v 1 ⋅ v 1 v 1 v 3 = x 3 − v 1 ⋅ x 3 v 1 ⋅ v 1 v 1 − v 2 ⋅ x 3 v 2 ⋅ v 2 v 2 ⋮ v p = x p − v 1 ⋅ x p v 1 ⋅ v 1 v 1 − ⋯ − v p − 1 ⋅ x p v p − 1 ⋅ v p − 1 v p − 1 \begin{aligned} \boldsymbol{v_1} &= \boldsymbol{x_1} \\ \boldsymbol{v_2} &= \boldsymbol{x_2} - \frac{\boldsymbol{v_1}\cdot\boldsymbol{x_2}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1}\\ \boldsymbol{v_3} &= \boldsymbol{x_3} - \frac{\boldsymbol{v_1}\cdot\boldsymbol{x_3}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1} - \frac{\boldsymbol{v_2}\cdot\boldsymbol{x_3}}{\boldsymbol{v_2}\cdot\boldsymbol{v_2}}\boldsymbol{v_2}\\ \vdots \\ \boldsymbol{v_p} & = \boldsymbol{x_p}-\frac{\boldsymbol{v_1}\cdot\boldsymbol{x_p}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1} - \cdots - \frac{\boldsymbol{v_{p-1}}\cdot \boldsymbol{x_p}}{\boldsymbol{v_{p-1}}\cdot\boldsymbol{v_{p-1}}}\boldsymbol{v_{p-1}} \end{aligned} v 1 v 2 v 3 ⋮ v p = x 1 = x 2 − v 1 ⋅ v 1 v 1 ⋅ x 2 v 1 = x 3 − v 1 ⋅ v 1 v 1 ⋅ x 3 v 1 − v 2 ⋅ v 2 v 2 ⋅ x 3 v 2 = x p − v 1 ⋅ v 1 v 1 ⋅ x p v 1 − ⋯ − v p − 1 ⋅ v p − 1 v p − 1 ⋅ x p v p − 1 Then, { v 1 , . . . , v p } \{\boldsymbol{v_1}, ..., \boldsymbol{v_p}\} { v 1 , . . . , v p } W W W
S p a n { v 1 , . . . , v k } = S p a n { x 1 , . . . , x k } f o r 1 ≤ k ≤ p Span\{\boldsymbol{v_1}, ..., \boldsymbol{v_k}\} = Span\{\boldsymbol{x_1}, ..., \boldsymbol{x_k}\} \ \ for \ \ 1\leq k \leq p S p a n { v 1 , . . . , v k } = S p a n { x 1 , . . . , x k } f o r 1 ≤ k ≤ p v j \boldsymbol{v_j} v j x j \boldsymbol{x_j} x j
p r o j S p a n { v 1 , . . . , v j − 1 } x j proj_{Span\{\boldsymbol{v_1}, ..., \boldsymbol{v_{j-1}}\}}\boldsymbol{x_j} p r o j S p a n { v 1 , . . . , v j − 1 } x j 입니다. 즉
v j = x j − p r o j S p a n { v 1 , . . . , v j − 1 } x j \boldsymbol{v_j} = \boldsymbol{x_j} - proj_{Span\{\boldsymbol{v_1}, ..., \boldsymbol{v_{j-1}}\}}\boldsymbol{x_j} v j = x j − p r o j S p a n { v 1 , . . . , v j − 1 } x j 입니다.
(1) Orthonormal basis
Orthogonal basis를 만들 수 있다면 orthonormal basis는 쉽게 만들 수 있습니다. orthogonal basis의 각각의 vector를 normalize시키면 바로 orthonormal basis가 됩니다.
$$
\boldsymbol{x_1} =\begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix}, \ \ \boldsymbol{x_2} = \begin{bmatrix}0 \\ 1 \\ 1 \\ 1\end{bmatrix}, \ \ \boldsymbol{x_3} = \begin{bmatrix}0 \\ 0 \\ 1 \\ 1 \end{bmatrix}
$$
위 벡터들은 linearly independent하므로
W = S p a n { x 1 , x 2 , x 3 } W = Span\{\boldsymbol{x_1}, \boldsymbol{x_2}, \boldsymbol{x_3}\} W = S p a n { x 1 , x 2 , x 3 } 의 basis는 { x 1 , x 2 , x 3 } \{\boldsymbol{x_1}, \boldsymbol{x_2}, \boldsymbol{x_3}\} { x 1 , x 2 , x 3 }
v 1 = x 1 \boldsymbol{v_1} = \boldsymbol{x_1} v 1 = x 1 으로 설정합니다. 두 번째로, v 2 \boldsymbol{v_2} v 2 x 2 \boldsymbol{x_2} x 2 S p a n { v 1 } Span\{\boldsymbol{v_1}\} S p a n { v 1 }
v 2 = x 2 − p r o j S p a n { v 1 } x 2 = x 2 − v 1 ⋅ x 2 v 1 ⋅ v 1 v 1 = x 2 − 3 4 v 1 = [ − 3 4 1 4 1 4 1 4 ] \begin{aligned} \boldsymbol{v_2} &= \boldsymbol{x_2} - proj_{Span\{\boldsymbol{v_1}\}}\boldsymbol{x_2} \\ &=\boldsymbol{x_2} - \frac{\boldsymbol{v_1}\cdot\boldsymbol{x_2}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1} \\ & = \boldsymbol{x_2} - \frac{3}{4}\boldsymbol{v_1} \\ &=\begin{bmatrix}-\frac{3}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \end{bmatrix} \end{aligned} v 2 = x 2 − p r o j S p a n { v 1 } x 2 = x 2 − v 1 ⋅ v 1 v 1 ⋅ x 2 v 1 = x 2 − 4 3 v 1 = ⎣ ⎢ ⎢ ⎢ ⎡ − 4 3 4 1 4 1 4 1 ⎦ ⎥ ⎥ ⎥ ⎤ 입니다. 분수 형태로 나와 계산이 어려우니, 위 벡터에 4 4 4
v 2 = [ − 3 1 1 1 ] \boldsymbol{v_2} = \begin{bmatrix} -3 \\ 1 \\ 1\\ 1 \end{bmatrix} v 2 = ⎣ ⎢ ⎢ ⎢ ⎡ − 3 1 1 1 ⎦ ⎥ ⎥ ⎥ ⎤ 을 사용하겠습니다. 위의 방법과 마찬가지로, v 3 \boldsymbol{v_3} v 3
v 3 = x 3 − p r o j S p a n { v 1 , v 2 } x 3 = x 3 − v 1 ⋅ x 3 v 1 ⋅ v 1 v 1 − v 2 ⋅ x 3 v 2 ⋅ v 2 v 2 = x 3 − 2 4 v 1 − 2 12 v 2 = [ 0 − 2 3 1 3 1 3 ] \begin{aligned} \boldsymbol{v_3} &= \boldsymbol{x_3} - proj_{Span\{\boldsymbol{v_1}, \boldsymbol{v_2}\}}\boldsymbol{x_3} \\ &=\boldsymbol{x_3} - \frac{\boldsymbol{v_1}\cdot\boldsymbol{x_3}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1} - \frac{\boldsymbol{v_2}\cdot\boldsymbol{x_3}}{\boldsymbol{v_2}\cdot\boldsymbol{v_2}}\boldsymbol{v_2} \\ &=\boldsymbol{x_3} - \frac{2}{4}\boldsymbol{v_1} - \frac{2}{12}\boldsymbol{v_2} \\ &=\begin{bmatrix}0 \\ -\frac{2}{3} \\ \frac{1}{3} \\ \frac{1}{3}\end{bmatrix} \end{aligned} v 3 = x 3 − p r o j S p a n { v 1 , v 2 } x 3 = x 3 − v 1 ⋅ v 1 v 1 ⋅ x 3 v 1 − v 2 ⋅ v 2 v 2 ⋅ x 3 v 2 = x 3 − 4 2 v 1 − 1 2 2 v 2 = ⎣ ⎢ ⎢ ⎢ ⎡ 0 − 3 2 3 1 3 1 ⎦ ⎥ ⎥ ⎥ ⎤ 이 됩니다. 역시 분수가 나와 위 벡터에 3을 곱한
v 3 = [ 0 − 2 1 1 ] \boldsymbol{v_3} = \begin{bmatrix}0 \\ -2 \\ 1 \\ 1 \end{bmatrix} v 3 = ⎣ ⎢ ⎢ ⎢ ⎡ 0 − 2 1 1 ⎦ ⎥ ⎥ ⎥ ⎤ 을 사용하겠습니다. 즉
{ v 1 , v 2 , v 3 } \{\boldsymbol{v_1}, \boldsymbol{v_2}, \boldsymbol{v_3}\} { v 1 , v 2 , v 3 } 가 W W W
∥ v 1 ∥ = 2 , ∥ v 2 ∥ = 2 3 , ∥ v 3 ∥ = 6 \|\boldsymbol{v_1}\| = 2, \ \ \|\boldsymbol{v_2}\| = 2\sqrt 3, \ \ \|\boldsymbol{v_3}\| = \sqrt 6 ∥ v 1 ∥ = 2 , ∥ v 2 ∥ = 2 3 , ∥ v 3 ∥ = 6 이므로
{ 1 2 v 1 , 1 2 3 , 1 6 v 3 } \{\frac{1}{2}\boldsymbol{v_1}, \frac{1}{2\sqrt 3}, \frac{1}{\sqrt6}\boldsymbol{v_3}\} { 2 1 v 1 , 2 3 1 , 6 1 v 3 } 가 W W W
지금까지 Gram-Schumidt process에 대해 알아보았습니다. 다음 포스트에서는 Least-Squares problems에 대해 알아보겠습니다. 질문이나 오류 있으면 댓글로 남겨주세요! 감사합니다!
Appendix : Proof of theorem
Theorem : The Gram-Schmidt Process
Given a basis { x 1 , . . . , x p } \{\boldsymbol{x_1}, ..., \boldsymbol{x_p}\} { x 1 , . . . , x p } W W W R n \mathbb R^n R n
v 1 = x 1 v 2 = x 2 − v 1 ⋅ x 2 v 1 ⋅ v 1 v 1 v 3 = x 3 − v 1 ⋅ x 3 v 1 ⋅ v 1 v 1 − v 2 ⋅ x 3 v 2 ⋅ v 2 v 2 ⋮ v p = x p − v 1 ⋅ x p v 1 ⋅ v 1 v 1 − ⋯ − v p − 1 ⋅ x p v p − 1 ⋅ v p − 1 v p − 1 \begin{aligned} \boldsymbol{v_1} &= \boldsymbol{x_1} \\ \boldsymbol{v_2} &= \boldsymbol{x_2} - \frac{\boldsymbol{v_1}\cdot\boldsymbol{x_2}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1}\\ \boldsymbol{v_3} &= \boldsymbol{x_3} - \frac{\boldsymbol{v_1}\cdot\boldsymbol{x_3}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1} - \frac{\boldsymbol{v_2}\cdot\boldsymbol{x_3}}{\boldsymbol{v_2}\cdot\boldsymbol{v_2}}\boldsymbol{v_2}\\ \vdots \\ \boldsymbol{v_p} & = \boldsymbol{x_p}-\frac{\boldsymbol{v_1}\cdot\boldsymbol{x_p}}{\boldsymbol{v_1}\cdot\boldsymbol{v_1}}\boldsymbol{v_1} - \cdots - \frac{\boldsymbol{v_{p-1}}\cdot \boldsymbol{x_p}}{\boldsymbol{v_{p-1}}\cdot\boldsymbol{v_{p-1}}}\boldsymbol{v_{p-1}} \end{aligned} v 1 v 2 v 3 ⋮ v p = x 1 = x 2 − v 1 ⋅ v 1 v 1 ⋅ x 2 v 1 = x 3 − v 1 ⋅ v 1 v 1 ⋅ x 3 v 1 − v 2 ⋅ v 2 v 2 ⋅ x 3 v 2 = x p − v 1 ⋅ v 1 v 1 ⋅ x p v 1 − ⋯ − v p − 1 ⋅ v p − 1 v p − 1 ⋅ x p v p − 1 Then, { v 1 , . . . , v p } \{\boldsymbol{v_1}, ..., \boldsymbol{v_p}\} { v 1 , . . . , v p } W W W
S p a n { v 1 , . . . , v k } = S p a n { x 1 , . . . , x k } f o r 1 ≤ k ≤ p Span\{\boldsymbol{v_1}, ..., \boldsymbol{v_k}\} = Span\{\boldsymbol{x_1}, ..., \boldsymbol{x_k}\} \ \ for \ \ 1\leq k \leq p S p a n { v 1 , . . . , v k } = S p a n { x 1 , . . . , x k } f o r 1 ≤ k ≤ p 수학적 귀납법을 통해 위 정리를 증명할 것입니다. 1 ≤ k ≤ p 1\leq k \leq p 1 ≤ k ≤ p
W k = S p a n { x 1 , . . . , x k } W_k = Span\{\boldsymbol{x_1}, ..., \boldsymbol{x_k}\} W k = S p a n { x 1 , . . . , x k } 로 W k W_k W k k = 1 k=1 k = 1
v 1 = x 1 \boldsymbol{v_1} = \boldsymbol{x_1} v 1 = x 1 로 정의할 수 있고, 따라서
S p a n { v 1 } = S p a n { x 1 } = W 1 Span\{\boldsymbol{v_1}\} = Span\{\boldsymbol{x_1}\} = W_1 S p a n { v 1 } = S p a n { x 1 } = W 1 을 만족합니다.
1 ≤ k 1\leq k 1 ≤ k W k W_k W k
{ v 1 , . . . , v k } \{\boldsymbol{v_1}, ..., \boldsymbol{v_k}\} { v 1 , . . . , v k } 라고 가정해봅시다.
이 때,
v k + 1 = x k + 1 − p r o j W k x k + 1 \boldsymbol{v_{k+1}} = \boldsymbol{x_{k+1}} - proj_{W_k}\boldsymbol{x_{k+1}} v k + 1 = x k + 1 − p r o j W k x k + 1 로 정의하면 v k + 1 \boldsymbol{v_{k+1}} v k + 1 W k W_k W k
W k + 1 = S p a n { x 1 , . . . , x k + 1 } W_{k+1} = Span\{\boldsymbol{x_1}, ..., \boldsymbol{x_{k+1}}\} W k + 1 = S p a n { x 1 , . . . , x k + 1 } 이므로 x k + 1 ∈ W k + 1 \boldsymbol{x_{k+1}}\in W_{k+1} x k + 1 ∈ W k + 1 p r o j W k x k + 1 ∈ W k + 1 proj_{W_k}\boldsymbol{x_{k+1}} \in W_{k+1} p r o j W k x k + 1 ∈ W k + 1
v k + 1 ∈ W k + 1 \boldsymbol{v_{k+1}} \in W_{k+1} v k + 1 ∈ W k + 1 이고, x k + 1 ∉ W k \boldsymbol{x_{k+1}} \notin W_k x k + 1 ∈ / W k v k + 1 ≠ 0 \boldsymbol{v_{k+1}}\neq0 v k + 1 = 0
{ v 1 , . . . , v k + 1 } \{\boldsymbol{v_1}, ..., \boldsymbol{v_{k+1}}\} { v 1 , . . . , v k + 1 } 은 orthogonal set이 되고, 따라서 W k + 1 W_{k+1} W k + 1
즉, k k k k + 1 k+1 k + 1 1 ≤ k ≤ p 1\leq k \leq p 1 ≤ k ≤ p