[CV] Harris Corner Detector

Harris Corner Detector

Harris의 corner detector의 기본원리는 다음과 같다.

위 그림 처럼 한 pixel을 중심에 놓고 작은 윈도우(window)를 설정한다.

$E(u, v) = \sigma_{x_k, y_k \in W} \begin{bmatrix}I(x_k + u, y_k + v) - I(x_k, y_k)\end{bmatrix}^2$

그런 다음 이 윈도우를 위 식과 같이 x축 방향으로 u만큼, y축 방향으로 v만큼 이동하고 윈도우 내의 픽셀 값들의 차이의 제곱의 합을 구한다. 이 식이 얼마나 픽셀이 이동했는지를 계산해주는 것

만약 corner라면, x, y축 방향 모두 많이 변화하여 E의 값이 커서 corner라고 인식

$E(u, v) \approx \sum{(x_k, y_k) \in W} (\frac{\partial I}{\partial x}u)^2 + (\frac{\partial I}{\partial y}v)^2 + 2\frac{\partial I}{\partial x}\frac{\partial I}{\partial y}uv$

테일러 공식으로 식을 이와 같이 확장할 수 있고 정리하면
$E(u, v) = \begin{bmatrix}u \quad v \end{bmatrix} \begin{bmatrix} \sum \frac{\partial I}{\partial x}^2 \quad \sum \frac{\partial I}{\partial x}\frac{\partial I}{\partial y} \\ \sum \frac{\partial I}{\partial x}\frac{\partial I}{\partial y} \quad \sum \frac{\partial I}{\partial y}^2\end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix}$
와 같이 됨

2x2 행렬을 M이라 부르고, eigen-decomposition을 하면 2개의 eigen value와 vector를 얻을 수 있는데 두 개의 eigen value 중에 더 큰 eigen value값과 연결된 eigen vector로 이미지의 변화가 가장 큼

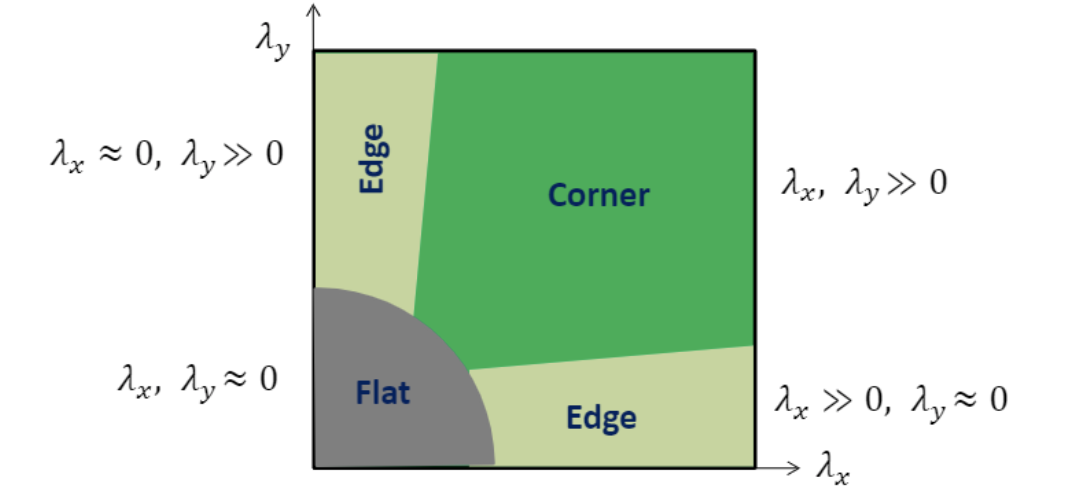
만약 두 방향으로 변화가 크면 corner 하나의 eigen value가 작고 또다른 value가 크다면 edge, 둘 다 0에 가까우면 flat으로 둠
2D 이미지의 경우에는 x, y값이 있기 때문에 2x2 matrix 나옴 그리고 rank가 2이기 때문에 eigen value 2개 밖에 나오지 않는다. (3D면 3개)

추가로, eigen value와 vector로 R을 사용해서 하는 방식도 있다.

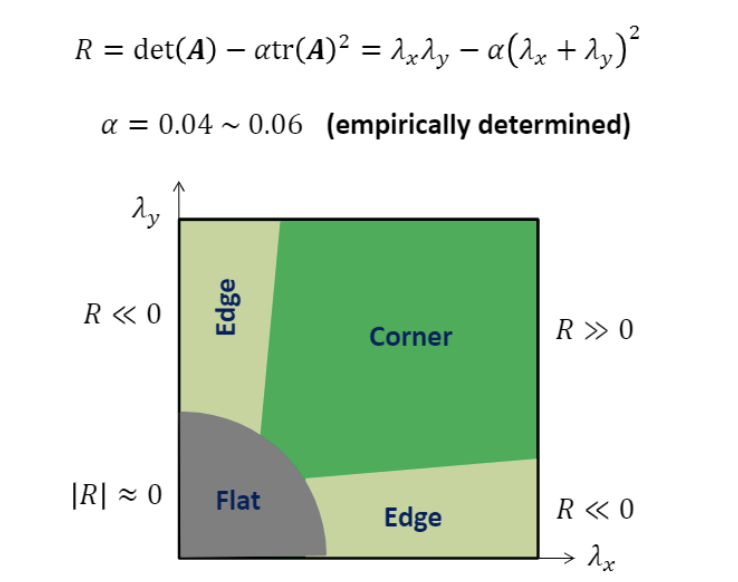
식을 통해서 eigen decompostion을 통해서 두 eigen value와 vector가 나왔을 때,
두 eigen value의 곱과 두 eigen value의 합을 제곱하고 알파를 곱한 값을 뺀 값 R이 0에 가까우면f lat 0보다 작으면 edge 0보다 크면 corner로 인식한다.

출처

[1] https://bskyvision.com/668