✦ EASER, 어떤 모델인가?
🔑 KEYWORD: 선형, Closed Form Solution, Item-Item Similarity
EASER는 선형 모델인 EASE를 발전시킨 모델이다.
최근 추천시스템에 딥러닝을 적용한 많은 모델들이 좋은 성능을 보여왔다. 그러나 타 AI분야(NLP, CV 등)와는 다르게 추천시스템에서는 적은 은닉층을 가진 모델이 더 좋은 성능을 보이는 경우가 많다. EASER는 그 중에서도 극단적으로 은닉층이 없는 선형 모델이다.
선형모델이기에 closed form solution을 가진다. 다시말해 ‘수식으로 표현할 수 있는’ 해를 가지며, 이를 ‘analytic 한 해를 가진다’ 고 표현하기도 한다.
전체적인 아이디어는 아이템과 아이템간의 유사도를 학습하여 사용자가 지금까지 소비한 아이템를 바탕으로 유사한 아이템을 추천해주는 것이다. item-item 쌍사이의 관계를 고려하여 사용자의 이전 상호작용 기록에서 두 아이템 이상의 조합이 더 높은 관련성을 갖는 경우를 식별한다. 때문에 CF같은 Neighbor Based 방법으로 볼 수도 있겠다. 이 때 아이템이 자기 스스로와 유사해지지 않도록 규제하여 일반화 성능을 올린다. 즉 weight matrix의 대각 성분 제로화하는 것. 아이템이 자기 자신과의 유사도가 과도하게 반영되면 다른 아이템들과의 상관관계를 제대로 학습하지 못할 수 있다. 따라서 이 규제는 모델이 다양한 상호작용 패턴을 학습하게 도와준다.
엄밀히 말하자면 이름에 나와있는 AE가 쓰이지는 않는다. AE처럼 유저 벡터를 압축하기 위해서 Dense Layer 가 존재하는가? 라고 묻는다면 그렇지 않다. 그렇기에 여타 딥러닝 기반의 추천시스템에 비해 상당히 간단한 모델이라고 할 수 있겠다. 대신, 출력 레이어의 B의 가중치를 저장한다.
✦ EASE 와는 어떻게 다를까?
Explicit FeedBack을 반영할 수 있는 EASER는
1️⃣ 먼저, 고차(Higher-order) 상호작용을 고려할 수 있다. 단순한 아이템 간의 쌍 관계만 학습하는 EASE와 다르게, 삼중(Triplet) 관계같은 고차 상호작용까지 학습하여 더욱 정밀한 추천을 제공할 수 있다. 2️⃣ 또한 네거티브(Negative)상호작용을 고려할 수 있다. 이는 사용자의 부정적인 선호도나 관심 부족을 표현하는 데 유용하다.
이를 통해 보다 복잡한 사용자 행동 양식과 선호도를 포착할 수 있다.
✦ EASER의 장점은?
선형 모델이기에 비교적 견고하고 계산적으로 효율적이며 간단하다. gradient descent 나 chain rule 을 사용하지 않아도 된다. 선형 계산위주라고 생각하면 된다. 그런데도 딥러닝이 판치는 추천시스템에서 SOTA를 달성했었다는 게 신기하다.
그리고 논문 제목에서도 알 수 있듯이 Sparse 한 데이터에 강하다.
그 외의 장점은,
1️⃣ 하이퍼 파라미터는 람다 하나이며 그 값에 따른 성능차이가 미미하다는 것
2️⃣ 그리고 빠르다 것(몇 시간/일이 걸리던 것을 몇 분 만에 훈련한다)
3️⃣ 흔하지 않은 고유한 항목 추천할 수 있기에 ‘발견’을 중시하는 추천분야에서 좋게 작용할 수 있겠다.
4️⃣ implicit, explicit 데이터 모두에 사용 가능하다고 한다
✦ 그래서 어떻게 작동할까?
- 수식에 등장하는 주요 인자는 다음 3가지이다.
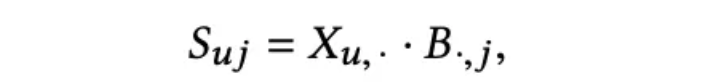
X(인풋행렬) → U X I (input data, binary)
B(가중치행렬) → I X I (model, weight, closed-form으로 훈련하는 모델)
⇒ 모델의 parameter, weight 이자 학습 대상이다.
⇒ diag(B)는 0으로 제한되는 것이 특징이다S(예측행렬) → U X I (X⋅B해서 나온 predict)
⇒ 우리의 최종 예측 타깃으로, user u가 아이템 i에 관심이 있을 확률 정보를 가진다
- 그럼 B를 구하려면(학습시키려면) 어떤 목적함수를 두어야할까? 수식은 다음과 같다.
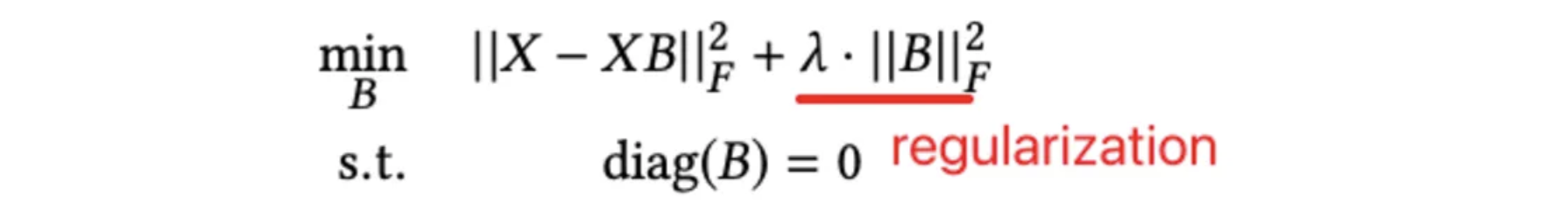
목적식에서 L1이 아닌 L2, 즉 square loss 를 사용한 이유는 앞서 언급했던 closed form solution 을 구할 수 있도록 하기 위함이다. 여기서 등장하는 람다가 아까 언급한 정규화 파라미터(모델의 유일한 파라미터..!)이다.
- 그럼 위의 목적함수를 만족하는 B에 대한 Closed Solution은 어떻게 구해질까? 증명은 생략하고 그 구체적인 프로세스만 정리해보았다.
- 그램 행렬을 작성 → G = X.t() * X
- G의 대각선을 따라 정규화 값(람다)을 추가
- P = G.inverse()
- B = -P/diagonals(P)
- B의 대각선을 0으로 설정
(여기서 G는 gram matrix로, co-occurence matrix이다.
예전에 강의에서 배웠던 A가 선택됐을 때 B, C가 선택되는 빈도를 item-item꼴로 나타낸 행렬)
