BFS
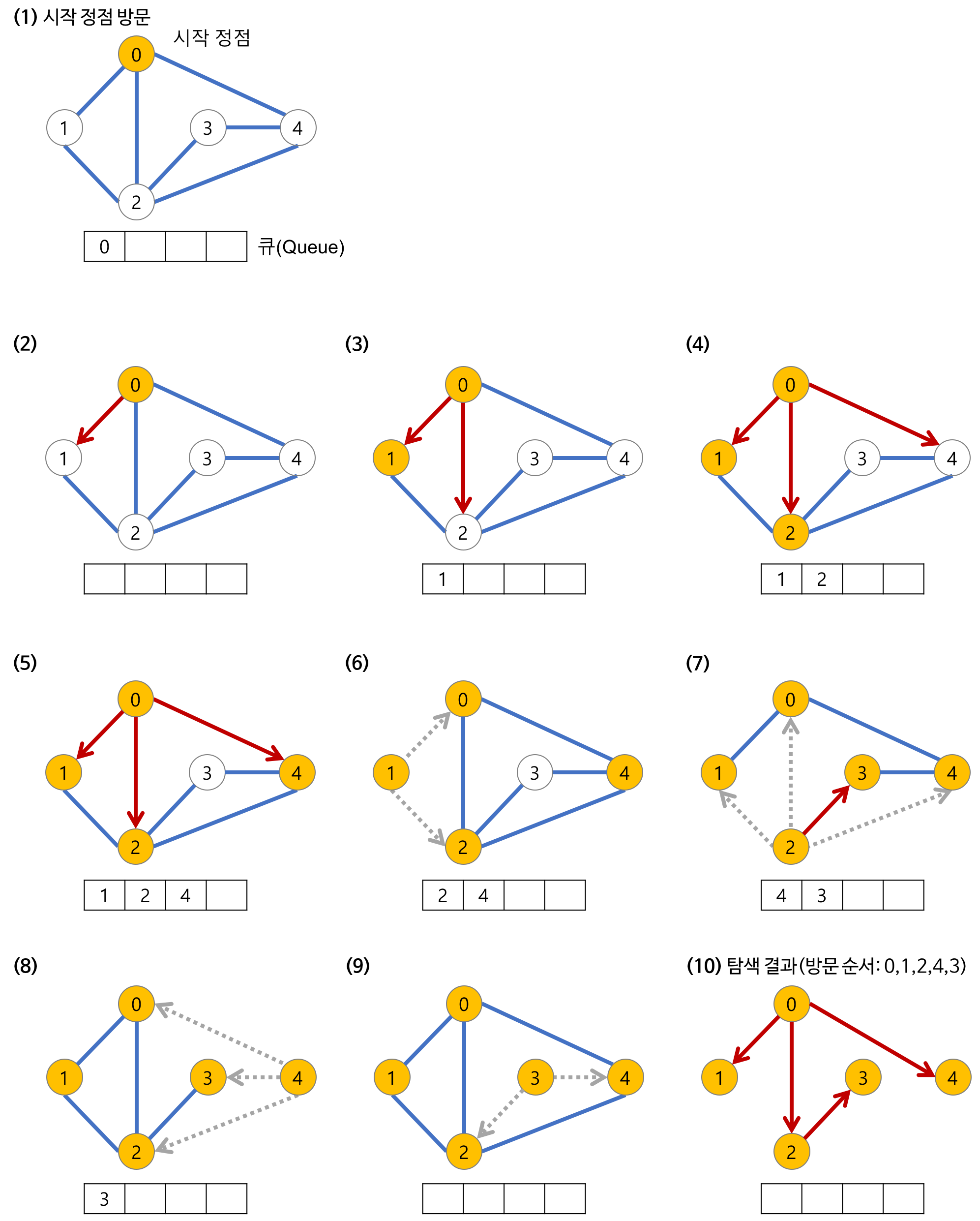
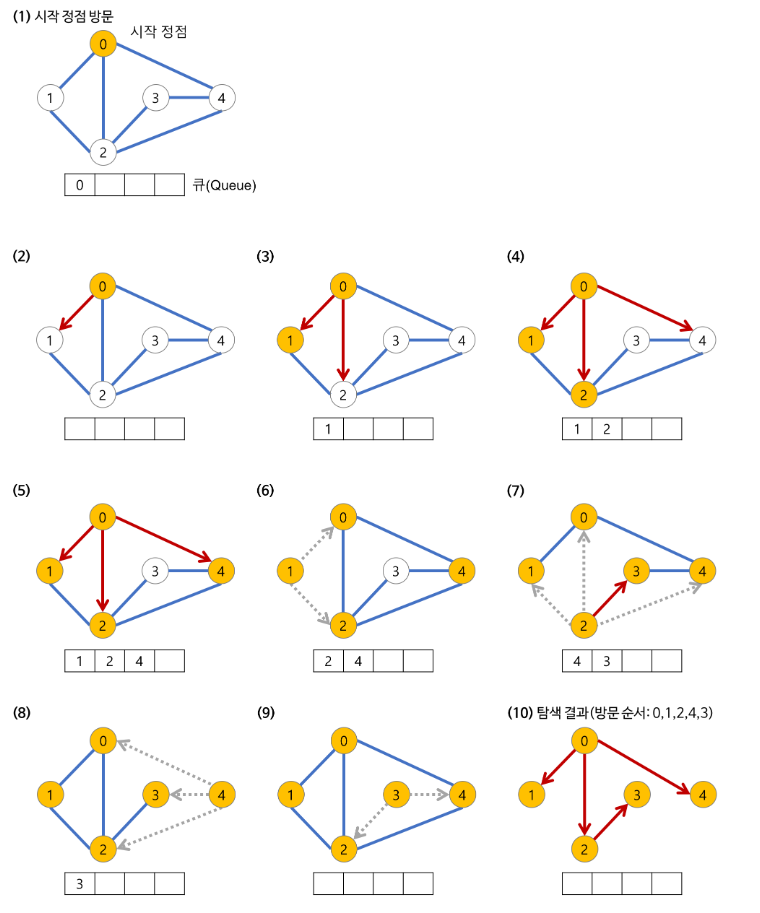
BFS(너비 우선 탐색)는 그래프 자료구조에서 사용되는 탐색 방법 중 하나입니다. 시작점으로부터 거리가 가까운 정점부터 먼저 탐색하는 방법입니다. 일반적으로 큐(Queue)를 이용하여 구현합니다.
BFS는 그래프의 최단 거리를 구하는 문제에서 매우 유용하게 사용됩니다. 또한 미로 찾기 등의 문제에서도 적용할 수 있습니다.
BFS를 구현하기 위해서는 다음과 같은 과정이 필요합니다.
- 시작 정점을 큐에 삽입합니다.
- 큐에서 정점을 하나 꺼내어, 해당 정점과 인접한 정점들을 모두 큐에 삽입합니다.
- 큐가 빌 때까지 위 과정을 반복합니다.
BFS는 일반적으로 인접 리스트(Adjacency List)를 이용하여 구현됩니다. 각 정점마다 연결된 정점들의 리스트를 가지고 있으며, 이를 통해 인접한 정점들을 찾을 수 있습니다.
BFS 코드를 살펴보면 아래와 같습니다.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
void bfs(vector<vector<int>> &adj, int start) {
queue<int> q;
vector<bool> visited(adj.size(), false);
q.push(start);
visited[start] = true;
while (!q.empty()) {
int curr = q.front();
q.pop();
cout << curr << " ";
for (int neighbor : adj[curr]) {
if (!visited[neighbor]) {
q.push(neighbor);
visited[neighbor] = true;
}
}
}
cout << endl;
}DFS
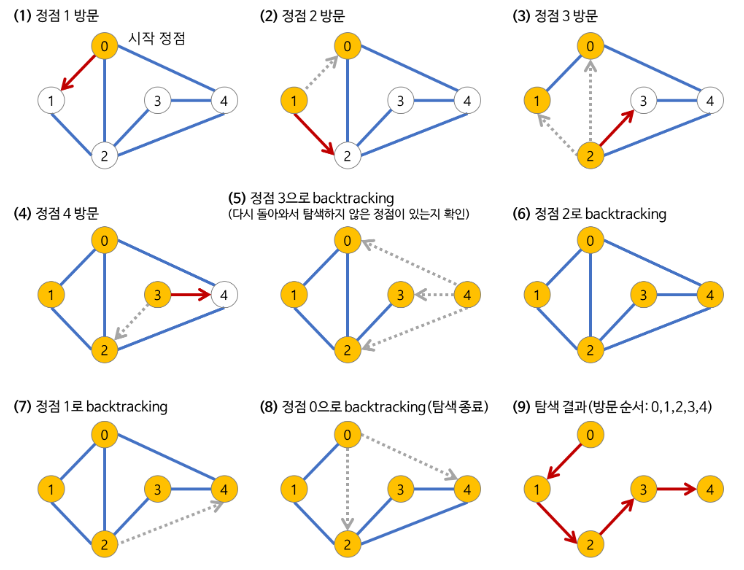
DFS(Depth First Search)는 그래프 탐색 알고리즘 중 하나로, 그래프의 깊은 부분을 우선적으로 탐색하는 알고리즘이다. 스택(Stack)이나 재귀 함수(Recursion)를 통해 구현할 수 있다.
DFS는 다음과 같은 특징을 가진다.
깊이 우선 탐색: 시작 정점으로부터 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색한다.
스택(Stack) 또는 재귀 함수(Recursion)로 구현된다.
BFS(Breadth First Search)보다 구현이 간단하지만, 최단 경로를 보장하지 않는다.
모든 정점을 방문하고 싶은 경우에 사용된다.
그래프의 구조를 파악할 때 유용하게 사용된다.
DFS의 구현 방법은 다음과 같다.
- 시작 정점을 방문한다.
- 현재 방문한 정점과 인접한 정점 중 방문하지 않은 정점을 찾는다.
- 방문하지 않은 정점이 있으면 해당 정점을 방문하고, 스택에 삽입한다.
- 방문하지 않은 정점이 없으면, 스택에서 최근에 삽입된 정점을 꺼낸다.
2~4 과정을 스택이 빌 때까지 반복한다.
DFS 코드를 살펴보면 아래와 같습니다.
#include <iostream>
#include <vector>
using namespace std;
void dfs(int node, vector<bool>& visited, vector<vector<int>>& graph) {
// Mark the current node as visited
visited[node] = true;
cout << node << " ";
// Recur for all adjacent nodes that are not visited
for (int i = 0; i < graph[node].size(); i++) {
int adj = graph[node][i];
if (!visited[adj]) {
dfs(adj, visited, graph);
}
}
}이미지 출처
