10. 이진 탐색 트리

이진 탐색 트리의 정의

• Binary Search가 항상 동작하도록 구현한 이진 트리
• 탐색 속도 극대화 시킨 자료구조
• 항상 부모 노드가 왼쪽 자식보다 크고 오른쪽 자식보다 작음

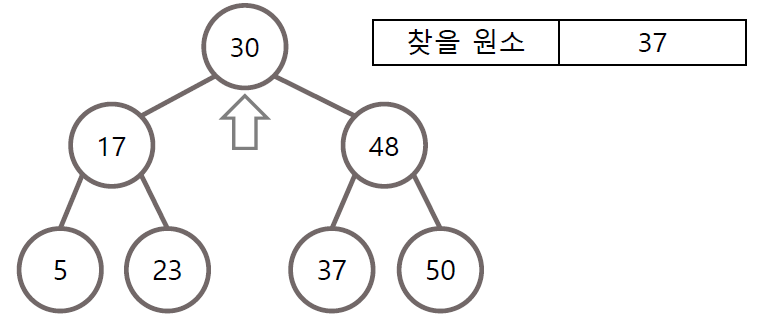
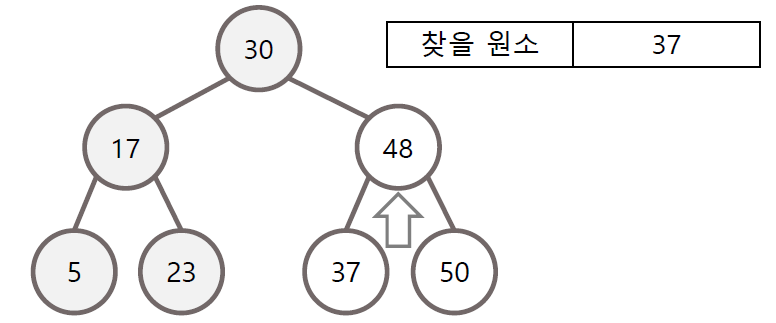
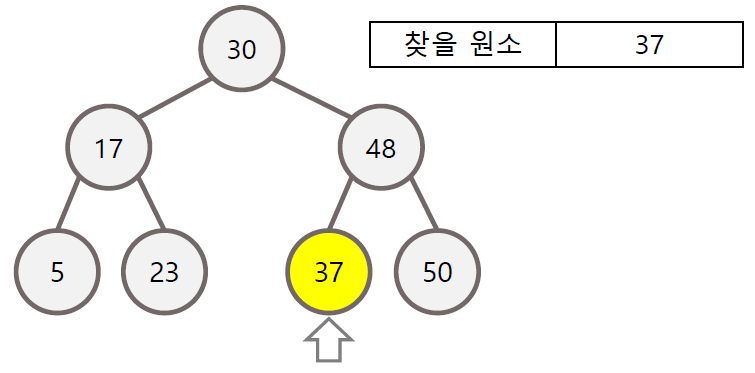
이진 탐색 트리의 탐색

• 한번 확인 할 떄마다 확인할 원소의 개수가 절반씩 줄어든다는 점에서 효율적
• 완전 이진 트리인 경우 탐색 시간에 O(log N)의 시간 복잡도를 가짐
• 탐색할 때 찾는 값이 부모 노드보다 작을 경우 왼쪽 자식으로, 클 경우 오른쪽 자식으로 방문

이진 탐색 트리의 삭제

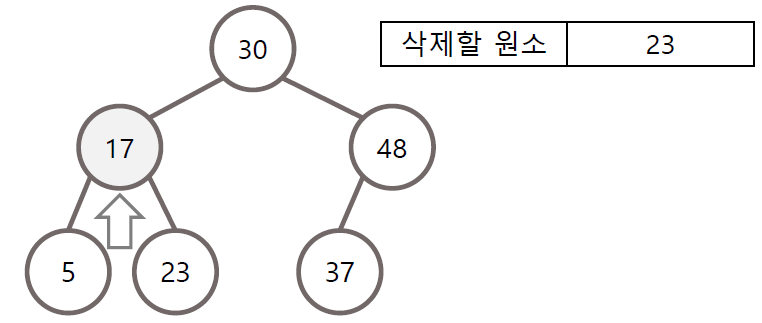
1) 자식이 없는 경우

삭제할 노드의 자식이 없는 경우 단순히 제거

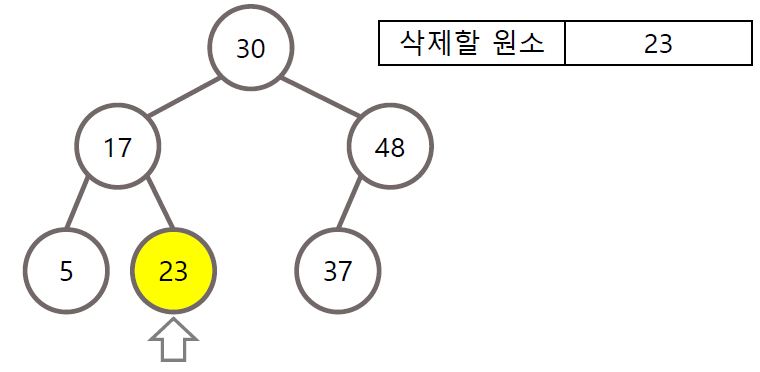
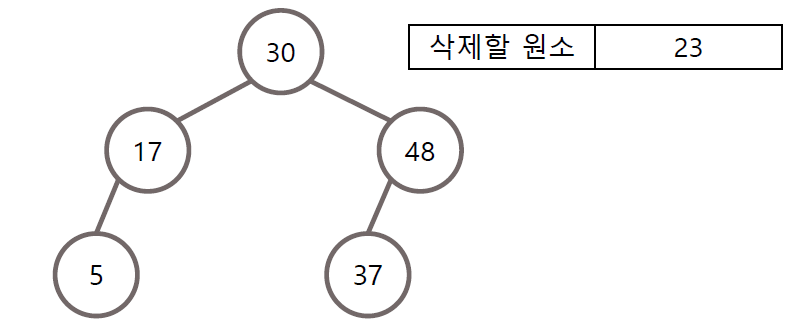
2) 자식이 하나만 존재하는 경우

삭제할 노드의 자식이 하나만 존재하는 경우 삭제할 노드의 자리에 자식 노드 대체

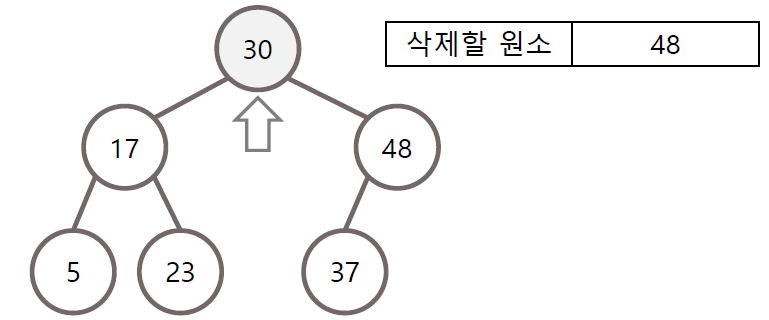
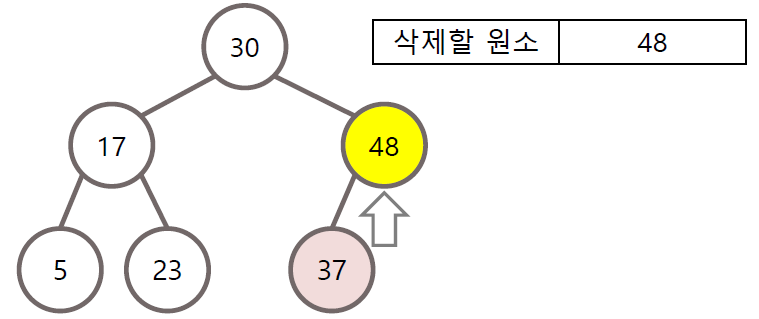
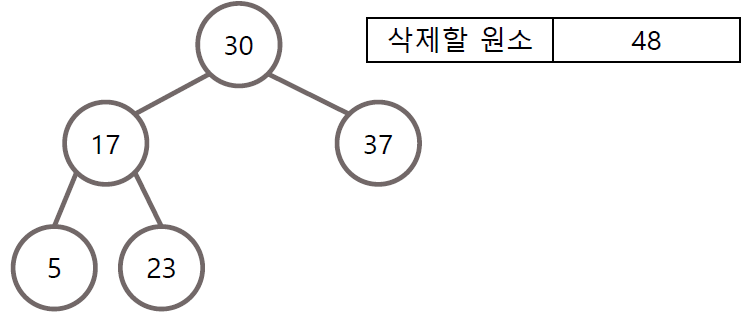
3) 자식이 둘 다 존재하는 경우

자식이 둘 다 존재할 경우 그 다음으로 삭제할 노드의 자리에 자기 다음으로 큰 노드 대체

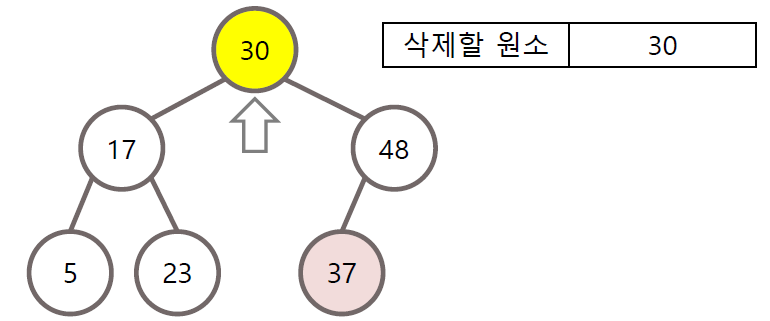
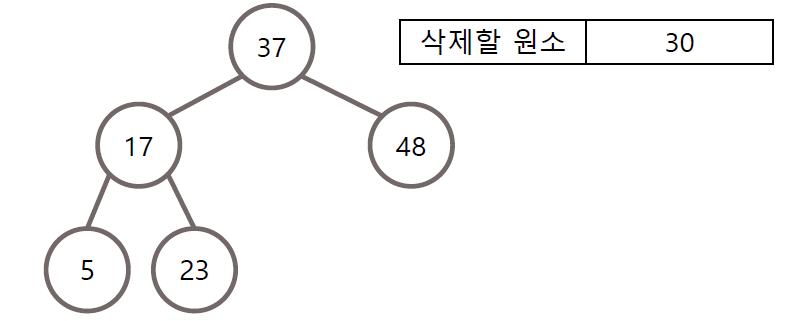
이진 탐색 트리의 구현

#include <stdio.h>
#include <stdlib.h>

// 노드 구현
typedef struct {
	int data;
	struct Node* leftChild;
	struct Node* rightChild;
} Node;

// 이진 탐색 트리의 삽입
Node* insertNode(Node* root, int data) {
	if (root == NULL) {
		root = (Node*)malloc(sizeof(Node));
		root->leftChild = root->rightChild = NULL;
		root->data = data;
		return root;
	}
	else {
		if (root->data > data) {
			root->leftChild = insertNode(root->leftChild, data);
		}
		else {
			root->rightChild = insertNode(root->rightChild, data);
		}
	}
	return root;
}

// 이진 탐색 트리의 탐색
Node* searchNode(Node* root, int data) {
	if(root == NULL) return NULL;
	if (root->data == data) return root;
	else if (root->data > data) return searchNode(root->leftChild, data);
	else return searchNode(root->rightChild, data);
}

// 이진 탐색 트리의 전위순회
void preorder(Node* root) {
	if (root == NULL) return;
	printf("%d ", root->data);
	preorder(root->leftChild);
	preorder(root->rightChild);
}

// 이진 탐색 트리의 가장 작은 원소 찾기
Node* findMinNode(Node* root) {
	Node* node = root;
	while (node->leftChild != NULL) {
		node = node->leftChild;
	}
	return node;
}

// 이진 탐색 트리의 삭제 함수
Node* deleteNode(Node* root, int data) {
	Node* node = NULL;
	if (root == NULL) return NULL;
	
	if (root->data > data) root->leftChild = deleteNode(root->leftChild, data);
	else if (root->data < data) root->rightChild = deleteNode(root->rightChild, data);
	else {
		// 두 자식 모두 존재 시
		if (root->leftChild != NULL && root->rightChild != NULL) {
			node = findMinNode(root->rightChild);
			root->data = node->data;
			root->rightChild = deleteNode(root->rightChild, node->data);
		}
		// 이외에 삼항 연산자로 처리
		else {
			node = (root->leftChild != NULL) ? root->leftChild : root->rightChild;
			free(root);
			return node;
		}
	}
	return root;
}

// 이진 탐색 트리 활용
int main(void) {
	Node* root = NULL;
	root = insertNode(root, 30);
	root = insertNode(root, 17);
	root = insertNode(root, 48);
	root = insertNode(root, 5);
	root = insertNode(root, 23);
	root = insertNode(root, 37);
	root = insertNode(root, 50);
	root = deleteNode(root, 30);
	preorder(root);
	system("pause");
	return 0;
}

이진 탐색 트리 정리

• 이진 탐색 트리의 성능을 최대로 끌어내기 위해서 완전 이진 트리에 가까워 지도록 설계
• 데이터의 개수가 N개 일 때 O(N)의 공간 소요

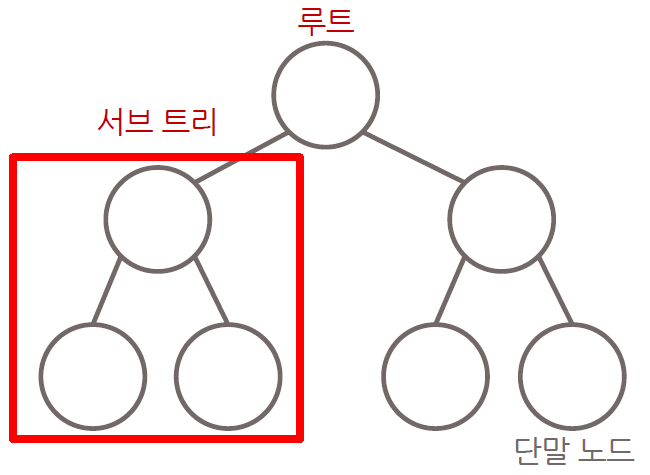
위와 같이 서브 트리도 완전 이진 트리가 되도록 이진 탐색 트리를 설계