Introduction

자연어처리, 컴퓨터비전 등 많은 분야에서 이미 Transformer의 활용성이 검증된 반면, 그래프 데이터에 대해서는 그 활용성이 확실히 검증되지 않았습니다. Transformer를 그래프 데이터에 잘 활용하려면 sequence modeling을 위해 설계된 Transformer에 그래프의 구조적 정보를 잘 인코딩하는 것이 중요할 것입니다.

이에 논문에서는 Centrality Encoding, Spatial Encoding, Edge Encoding 을 도입한 Graphormer를 소개합니다. 논문에서는 Graphormer가 위 인코딩들을 Self Attention 연산 안에 추가함으로써 그래프의 구조적 정보를 모델에 반영할 수 있다고 주장하며, 이들이 반영하는 바는 아래와 같습니다.

1. Centrality Encoding : 각 노드의 중요도 반영
2. Spatial Encoding : 그래프 안에서 노드의 공간 정보를 반영
3. Edge Encoding : 노드 간 연결(엣지) 정보를 반영

Method

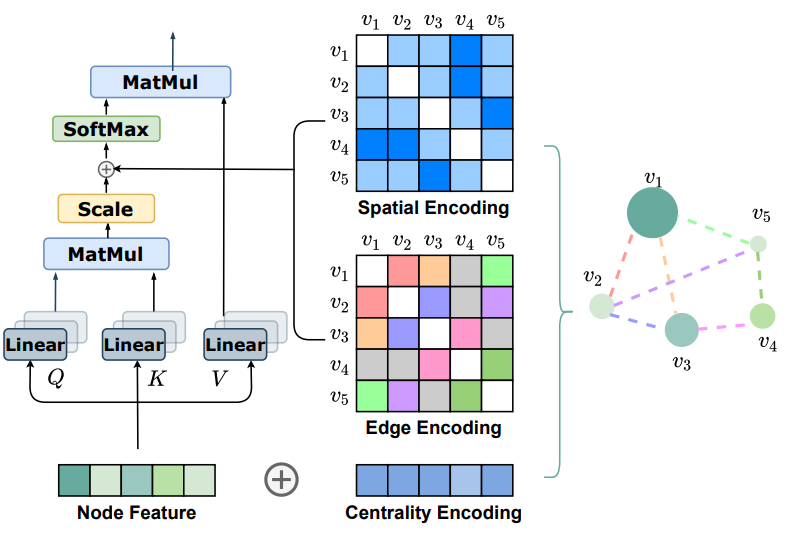
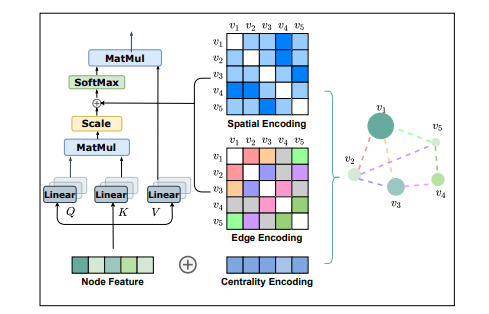
Graphormer는 기본적으로 Transformer의 Encoder를 사용하는데, 기존 Transformer와 달리 세 가지 인코딩(Centrality, Spatial, Edge)이 Self Attention Layer 안에 위 figure와 같이 반영되어 있습니다. 각 인코딩에 대한 설명은 아래와 같습니다.

Centrality Encoding

기존 Attention 메커니즘은 노드 간의 의미적 연관(semantic correlation)만을 고려하지만, 그래프 내 노드들은 그 중요성이 각각 다릅니다. eg) 소셜 네트워크에서 일반인과 유명인의 차이. 그러므로 그래프 분야에서는 노드의 중요성을 평가하는 척도 로 여러 node centralities를 사용하는데, Graphormer는 이들 중 in/out degree를 활용하는 degree centrality를 self attention에 반영합니다.

Centrality Encoding은 노드의 in degree, out degree를 기반으로 정해진 길이의 임베딩 벡터$z^{-}_{deg^-(v_i)}$ 와 $z^{+}_{deg^+(v_i)}$를 만들어 Attention Layer의 input으로 들어가는 node feature $x_i$에 더해줌으로써 동작합니다.

$h^{(0)}_i =x_i + z^-_{deg^-(v_i)}+z^{-}_{deg^+(v_i)},\;\;z^-,z^+ \in \mathbb R^d$

Centrality Encoding이 적용된 Self-attention 연산은 아래와 같습니다.

$A_{ij}=\frac{(h_iW_Q)(h_iW_k)^T}{\sqrt{d}}$

Spatial Encoding

기존 Transformer 구조는 Positional Encoding이나 Positional Embedding을 적용하여 시퀀스 내 공간정보(locality)를 표현합니다. 하지만 그래프 데이터는 일반적인 데이터와 달리 locality를 정의하기 어려워 그래프 내 공간정보를 인코딩하기 난감합니다.
이에 Graphormer는 새로운 Spatial Encoding을 제안하는데, 이는 요약하자면 '두 노드 간 공간 정보 기반의 임베딩 스칼라를 생성' 하는 방법입니다. 자세 설명은 아래와 같습니다.

먼저, 그래프 $G$ 내의 두 노드 $v_i,v_j$간의 연결 관계를 표현할 수 있는 함수 $\phi(v_i,v_j)\rightarrow \mathbb R$ 를 정의합니다.
- 논문에서는 $\phi$를 두 노드 간 최단거리(SPD)로 설정했습니다.
- 최단거리를 구할 때에는 Floyd-Warshall 알고리즘을 이용합니다.
- 두 노드가 연결되지 않았다면 -1과 같은 값으로 mask를 씌웁니다.

이렇게 구한 상수 $\phi(v_i,v_j)$값으로 인덱싱되는 학습 가능한 스칼라 $b_{\phi(v_i,v_j)}$를 self attention 연산에서 bias term으로 이용(모든 layer에서 공유)함으로써 self attention 연산이 두 노드 간 공간 정보를 담게 됩니다.

Centrality Encoding과 Spatial Encoding이 적용된 self-attention 연산은 아래와 같습니다.

$A_{ij}=\frac{(h_iW_Q)(h_iW_k)^T}{\sqrt{d}}+b_{\phi(v_i,v_j)}$

Edge Encoding

그래프 데이터에서는 노드 뿐만 아니라 엣지 자체도 유의미한 정보를 갖는 경우가 많습니다. 그러므로 그래프의 특성을 표현하는 데 있어서 엣지를 잘 인코딩하는 것이 중요한데, 기존 방법론은 아래와 같습니다.

1. 엣지의 feature를 해당 엣지로 연결된 두 노드의 feature에 더해준다.
2. 이웃 노드의 정보를 Aggregate하는 과정에서 연결된 엣지의 feature도 함께 aggregate한다.

그러나 이러한 방법은 전체 그래프의 representation을 구할 때 엣지의 정보를 효과적으로 이끌어낼 수 있는 방법이라 볼 수 없습니다. 그러므로 논문에서는 다음과 같은 새로운 Edge Encoding을 제안합니다.

두 노드 $v_i, v_j$ 사이의 가장 짧은 경로 $SP_{ij}=(e_1,e_2,...,e_N)$이 있을 때, 경로 안의 모든 엣지에 대해 해당 엣지에 대응하는 임베딩 벡터 $w^E_n$과 엣지 feature $x_{e_n}$의 내적값의 평균을 계산합니다.

$A_{ij}=\frac{(h_iW_Q)(h_iW_k)^T}{\sqrt{d}}+b_{\phi(v_i,v_j)}+c_{ij},\;\;where\;c_{ij}=\frac{1}{N}\sum\limits_{n=1}^{N}x_n(w^E_n)^T$

• $x_{e_n}$ n번째 edge의 edge feature
• $w^E_n$ : n번째 edge에 대응하는 임베딩 벡터

Implementation Details

Graphormer는 그래프의 특성을 반영하기 위한 인코딩 이외에도 Pre-layernorm을 적용하고 Special Node를 도입하여 모델의 성능을 높였습니다.

Pre-Layernorm

일반적인 Transformer Encoder에서 Layer Normalization(LN)은 multi-head self-attention(MHA) layer와 feed-forward layer(FFN)를 통과한 이후에 각각 적용됩니다. Graphormer는 이와 다르게 LN이 MHA와 FFN를 통과하기 전에 각각 적용됩니다.

기존 Transformer Encoder Layer

• $h^{'(l)} = LN(MHA(h^{(l-1)})+h^{(l-1)})$
• $h^{(l)} = LN(FFN(h^{'(l)})+h^{'(l)})$
  Graphormer Layer
• $h^{'(l)} = MHA(LN(h^{(l-1)}))+h^{(l-1)}$
• $h^{(l)} = FFN(LN(h^{'(l)}))+h^{'(l)}$

이처럼 layer normalization이 MHA나 FFN 이전에 적용되는 구조는 최적화에 더 용이하므로 최근의 Transformer Based Model에서 흔히 사용되는 구조라고 합니다.

Special Node

Bert에서 문장 전체의 representation을 담는 [CLS]토큰과 같이, Graphormer에는 Graph Representation $h_G$을 담기 위한 가상의 노드 $[\textbf{VNode}]$가 존재합니다. $[\textbf{VNode}]$는 모든 노드와 연결되어 있으며 Aggregate-Combine step에서 다른 노드들과 같이 representation이 업데이트됩니다. 하지만 $[\textbf{VNode}]$와 다른 노드 간의 엣지는 실제 연결이 아닌 가상의 연결이므로 이에 대응하는 Spatial Encoding $b_{\phi(v_i,[\mathbf{VNode}])}$, $b_{\phi([\mathbf{VNode}],v_i)}$의 값을 특정 학습 가능한 스칼라로 구분합니다.

Experiments

논문에서는 Graphormer를 이용해 Graph Classification, Graph Regression Task를 수행했습니다. 모델은 크게 세 가지 scale로 나뉩니다. 아래 세 가지 모델 이외에 $\textbf{Graphormer}-{\textbf{FLAG}}$는 모델의 크기가 크고 데이터셋의 크기가 작아 생길 수 있는 오버핑 문제를 완화하기 위해 그래프 데이터 증강 방법인 $\textbf{FLAG}$를 적용한 모델입니다.

Graphormer ($L=12$, $d=768$)
$\textbf{Graphormer}_{\textbf{small}}$ ($L=6$, $d=512$)
$\textbf{Graphormer}_{\textbf{slim}}$ ($L=12$, $d=80$)

Results

Graphormer는 PCQM4M-LSC, MolPCBA, MolHIV, ZINC Dataset에서 SOTA를 달성했습니다. 아래는 PCQM4M-LSC Datatset에 대한 Table입니다.

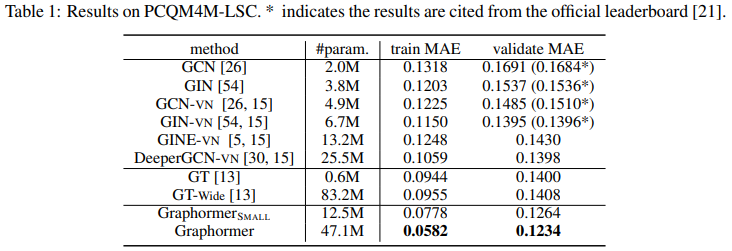
$\textbf{Graphormer}$ 와 $\textbf{Graphormer}_{\textbf{small}}$ 모두 기존 SOTA Model보다 작은 MAE를 보입니다.

Ablation Studies

논문에서 제시한 세 가지 인코딩의 성능을 확인하기 위해 PCQM4M-LSC Dataset으로 Ablation Study를 한 결과는 아래와 같습니다.

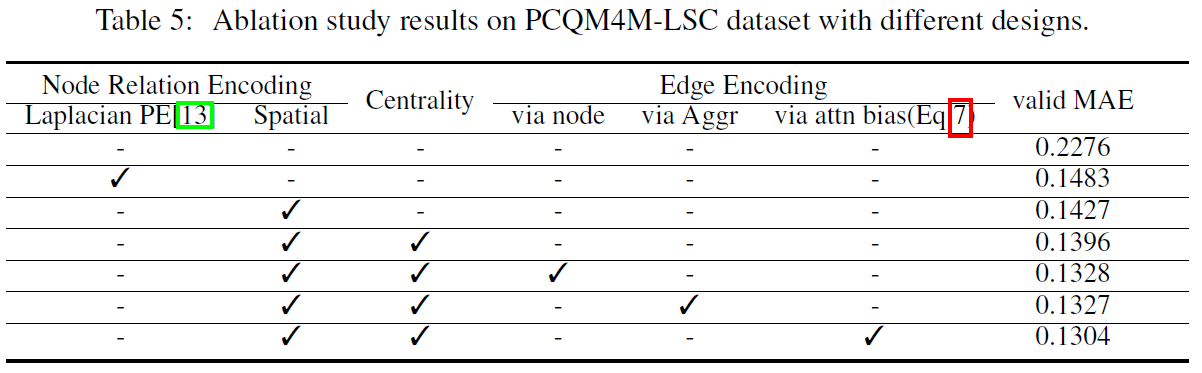
Spatial Encoding

논문에서 제시한 SPD(논문에서는 Floyd-Warshall 알고리즘 이용)를 이용한 Spatial Encoding의 성능을 확인하기 위해, 아래 세가지 세팅에서의 Validation MAE를 비교하고, 논문에서 제시한 방법이 가장 좋은 성능을 냄을 확인했습니다.

1. 아무런 Spatial Encoding을 사용하지 않음
2. Laplacian PE 사용
   • Degree Matrix에서 Adjacency Matrix를 뺀 Laplacian Matrix를 이용하는 방법입니다.
3. SPD를 이용한(논문에서 제시한) Spatial Encoding을 사용

Centrality Encoding

Table을 보면, $deg^+$, $deg^-$를 이용한 centrality encoding이 MAE를 많이 낮췄음을 알 수 있습니다.

Edge Encoding

기존에 Edge feature를 encode하기 위해 노드 feature에 해당 노드에 붙어 있는 edge feature를 더해주거나, 이웃 노드의 정보를 aggregate할 때 edge feature를 함께 aggregate하는 방법에 비해 논문에서 제시한 Edge encoding이 성능 향상에 도움이 됨을 확인할 수 있습니다.

Pytorch Implementation

Graphormer의 Pytorch 구현 코드는 Gihtub에서 확인하실 수 있습니다.

Conclusion

Graphormer는 Tansformer Architecture로 Graph의 representation을 효과적으로 이끌어내기 위한 방법을 제시하면서 여러 벤치마크에서 SOTA를 달성했지만, Self-Attention 연산의 복잡도가 $O(N^2)$이고 Spatial Encoding과 Edge Encoding 또한 큰 그래프에 대해 적용하기 힘든 점 등 한계가 있습니다.
이에 후속 연구로는 Self-Attention을 그래프 구조에 효율적으로 적용하기 위한 방법들이 많이 제시되는데, Node Classification Task에서 전체 그래프가 아닌 기준 노드 주변의 Subgraph를 추출하는 연구나 노드 샘플링 전략을 학습하여 샘플링된 노드들로 self-attention 연산을 하는 연구 등이 이에 해당합니다. 후자의 경우에는 [링크]에 간단히 정리되어 있습니다.