Introduction

기존 Graph Transformer Architecture 한계

• Computationally inefficient
• Full Attention Mechanism이 전체 그래프 특성과 상관 없는 노드 정보를 많이 반영(noise).
  -> 그래서 기존 Graph Transformer Architecture들은 Receptive Field 줄이기 위해 Node Sampling Method 이용.
  • 고정된 node sampling은 그래프의 성질(Homopily/Heterophily)를 고려하지 못하므로 중요하지 않은 노드를 sampling할 우려가 있음.
  • 대부분의 sampling methods는 locah neighbor에 집중해 long range depedency를 잘 capture하지 못함 -> 그래프의 global context를 반영하기 어려움.

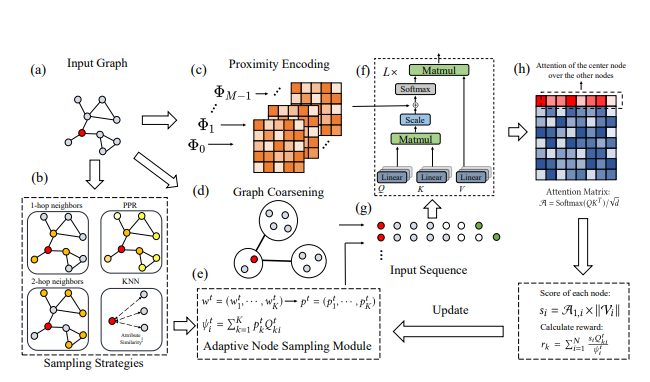
ANS-GT

Adaptive Node Sampling을 적용한 ANS-GT

• 여러 sampling methods의 최적의 조합을 선택하는 문제를 Multi-Armed Bandit Problem으로 보고 sampling methods에 대한 가중치를 최적화.
• 특정 sampling method에서의 sampling probability distribution과 attention weight distribution이 비슷할수록 해당 method에 큰 reward를 주는 방식으로 최적화.
  -> 노드를 adaptive하게 sample한다.
  

Hierarchical Attention Scheme

• 그래프를 Coarsen(Supernodes, Global nodes)로 통합 -> 이후 Attention -> long range dependency를 capture할 수 있음.

Preliminaries & Proposed Methods

Motivating Observations : Adaptive Node Sampling의 필요성

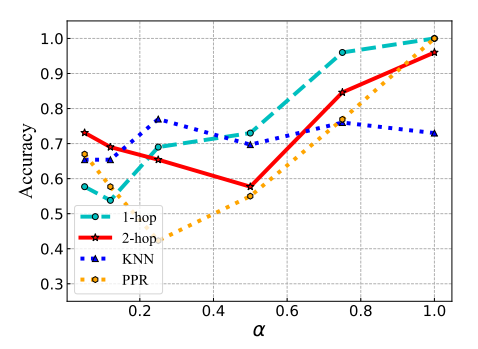
• Graph Properties(e.g Homopily / Heterophily)에 따라 유효한 Sampling Method가 달라짐을 보여준다. $\alpha$ (같은 class의 노드끼리 연결된 정도, 0~1)값 변화에 따라 각 sampling method에서의 Node Classification Accuracy가 가파르게 변한다.
  -> Adaptive Node Sampling 필요

Adaptive Node Sampling

Intuition

• Node를 잘 Sample하는 행동이 Learning Performance에 주는 영향은 time-sensitive하다.
• 모델 학습 과정에서 각 Sampling Method에 주는 Reward또한 Iteration과 무관하지 않다.
  -> Multi-Armed Bandit Problem으로 접근
  

Procedure

$w^t = (w^t_1, \cdots , w^t_K)$

• 위와 같이 Iteration t에서 K개의 Node Sampling Method에 대한 가중치 벡터를 $w^t$로 놓는다.
• 실제 활용할 때에는

  $p^t = (p^t_1, \cdots , p^t_K)\ where \; p^t_k \in [p_{min}, 1]$

로 scale해 사용한다.

• 이후 $K$개의 sampling method에서 모든 $n$개 node에 대한 Sampling Probability를 담은 $Q^t$를 생성

$Q^t_{ki}$ : $k_{th}$ sampling method에서 $i_{th}$ node가 sample될 확률

-> 최종적으로 $i_{th}$ node를 Sample할 확률 $\psi^t_i$는 다음과 같이 계산된다.

$\psi^t_i = \sum^K_{k=1}p^t_kQ^t_{ki}$
: 각 method를 선택할 확률 * 해당 method에서 특정 $i_{th}$ 노드가 sample될 확률의 가중합

이렇게 구한 확률을 바탕으로 $N$개의 노드를 sample해서 Transformer Archetecture의 input으로 넣고, 그 과정에서 나온 Attention Weight Matrix $A$의 첫 row $A_1$을 사용해 각 노드의 significance score $s_i$를 구한다.

$s_i = A_{1,i}* \left|\left|v_i\right|\right|$
$\left|\left|v_i\right|\right|$는 node의 significance를 반영하기 위한 node representation의 L2 norm

이후 $s_i, \;\psi^t_i, \;Q^t_{ki}$를 이용해 $k_{th}$ sampling method에 대한 reward $r_k$를 계산한다.

$r_k = \sum^N_{i=1} \frac{s_iQ^t_{ki}}{\psi^t_i}\;=s\cdot\frac{Q^t_k}{\psi^t}$

위 식처럼 결국 $r_k$는 $s$와 $\frac{Q^t_k}{\psi^t}$의 내적이 된다.

헌데, $\psi^t$는 모든 $Q^t_{ki}$의 가중합(가중치 : $p^t_k$) 이므로 noramlized sampling probability distribution으로 볼 수 있으므로 특정 sampling method $a$가 다른 method들보다 큰 reward를 가지려면 $Q^t_a$가 $s$와 비슷해야 $r_a$가 다른 $r_k$보다 커질 것이다.
-> 해당 reward로 sampling strategy를 최적화한다는 것은 결국 Attention weight가 높은 노드를 잘 뽑도록 sampling strategy를 update하는 것과 같다. 다만 계산 효율을 고려해 이러한 업데이트는 매 epoch마다가 아닌 정해진 T epoch마다 수행한다.

Hierarchical Attention Scheme

전처리 과정에서 그래프를 정해진 개수의 supernodes $n_s$, global nodes $n_g$로 coarsen한 후 해당 노드들 + sample된 노드들을 이용해 Attention을 수행하는 방법으로 long-range dependency를 수행한다.

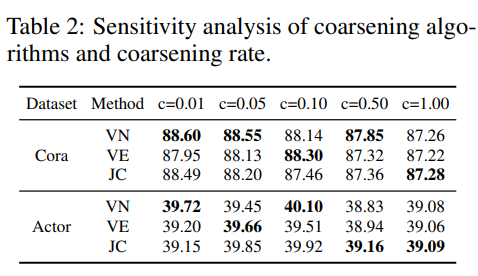
• Coasening algorithms : Variation Neighborhoods, Variation Edges, Algebraic
• Coarsening rate $c$, coarsening algorithm 따라 모델 성능이 달라진다.
  

Architecture

Algorithms

Experiments

Benchmarks

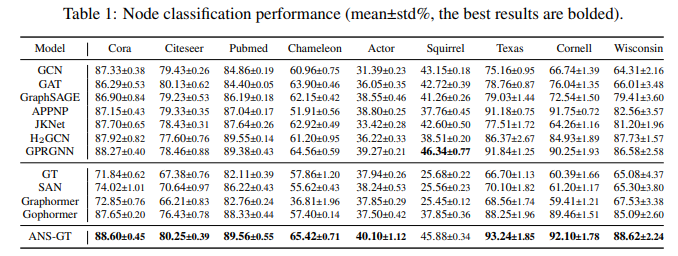
Node Classification Task에서 많은 benchmark datasets에 대해 Sota를 달성했다. 기존 graph transformer뿐만 아니라 GNN 모델들과 비교해도 좋은 결과를 보인다.

Sampling weights의 변화

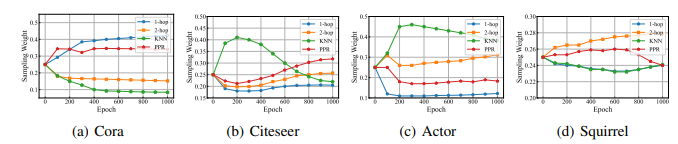
각 benchmark dataset에서 4개의 Sampling Methods(1-hop / 2-hop neighbor, KNN, PPR)의 Sampling weights가 학습 초반에는 급격히 변하다 점점 안정화되는 경향 보임.

Ablation : Effectiveness of Adaptive Node Sampling

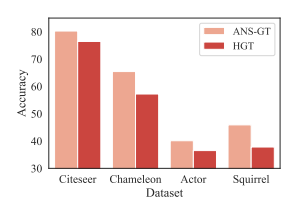
Apdaptive Node Sampling을 적용하지 않고 Hierarchical Graph Transformer만 적용한 모델 Vs ANS-GT의 Node Classfication Accuracy 비교
-> Adaptive Node Sampling이 Fixed Node Sampling보다 좋다!

Time Complexity

기존 GT Architectures에 비해 추가된 요소가 많아 계산비용이 높지 않을까 우려되지만, 그렇지 않다는 것을 증명함.

• Graph Coarsening에 대한 Complexity는 $O(n)$이며, Attention을 한 번 수행할 때 Complexity는 $O(nS(N+n_s+n_g)$이다.
  - * $n_s$, $n_g$는 각각 super node와 global node를 뜻하며, Graph coarsening 이전에 정하는 하이퍼파라미터이다.
  

Contributions

• 별도의 Model Modifing 없이 Sampling Method의 수정과 사전 Graph Coarsening만으로 높은 performance 이끌어냄.
• 해당 파이프라인에 맞춰 다양한 sampling method, graph coarsen method를 적용해 추후 모델 발전 가능성이 있음.

Limitations

1. 하이퍼파라미터 개수가 많음.

논문에서 제시한 4개의 주요 하이퍼파라미터
1. Layer의 개수
2. $n_s$ : supernode의 개수
3. $n_g$ : global node의 개수
4. $S$ : number of augmentations

++ 이외에도 Coarsening rate $c$, Coarsening Algorithm과 Sampling Method의 선택 등 Acc에 영향 주는 요소가 많음.

Question about Graph Coarsening

Diffpool 등 Multi-scale graph coarsening method가 있는데 왜 굳이 전처리 과정에서 deterministic한 method로 한 번에 graph coarsening을 했을까?

• 첫 Transformermer Layer에부터 coarsend graph를 input으로 넣어줘야 초반에 유의미한 long-range dependency를 잘 capture할 수 있기 때문이 아닐까..?