> 이 글은 스탠퍼드대학교 Andrew Ng 교수님의 강의를 수강한 것을 토대로 작성한 글입니다

📌 Deciding What to Try Next

• 가설을 예측한 것에서 오류가 발생한 경우 해결 방법
  1. 더 많은 학습 데이터 사용하기
  2. features 줄이기
  3. features 추가하기
  4. polynomial(고차원) 항 추가하기
  5. lambda값 줄이기
  6. lambda값 늘이기

• 위 방법을 무조건적으로 사용하는 것이 아니라,
  무엇이 문제인지 명확히 파악하여 해결책을 사용해야 함
  따라서 Machin learnning diagnostic(기계학습 진단)이 필요

📌 Evaluating a Hypothesis

가설 평가

• Overfitting(과적합)
  

  • 과적합 발생 확인 방법 = test셋 사용
    
    위와 같은 Dataset이 주어졌을 때,
    Dataset의 자료들 중 무작위로 뽑아 70%는 Training set으로 Training에 사용하고 30%는 Test set으로 Test에 사용
    여기서 Training set과 Test set 전혀 다른 자료임

• linear regression(선형 회귀)
  

  1. Training set에서 parameter θ를 학습하여 J(θ)의 Training error를 최소화 ( 보유 Data의 70% 사용 )

  2. 테스트 오차 계산

• logistic regression(로지스틱 회귀)
  

1. Training set에서 parameter θ를 학습하여 J(θ)의 Training error를 최소화 ( 보유 Data의 70% 사용 )

2. 테스트 오차 계산

3. 오분류율

   • hθ(x) >= 0.5 and y = 0
     hθ(x) < 0.5 and y = 1
     -> err (hθ(x0, y) = 1

   • 즉, 1일 가능성이 더 높았지만 실제로는 0
     0일 가능성이 높았지만 실제로는 1

📌 Model Selection and Train/Validation/Test Sets

모델 선택과 학습 / 검증 / 테스트 셋

Model Selection 문제 = 다항식의 차수, 정규화 파라미터의 값 또는 피처를 값을 어떻게 설정해야 할지에 대한 문제

• 각 차수에 대한 가설함수를 설정하고 훈련을 시킨 후 적절한 차수 결정

  1. 변수 d를 최고차항의 차수로 설정
  2. d에 대해 훈련을 실행 -> d에 대한 서로 다른 θ값을 얻을 수 있음
  3. θ을 Jtest(θ)에 적용 -> 가장 낮은 오차를 가지는 가설함수 선택
  4. 위의 예시에서는 5차항이 선택됨
     but, 새로운 Data가 들어오면 선택된다는 보장 X

• 문제를 해결하기 위해 Train/Validation/Test Sets으로 나눠 계산
  (비율 - 60%, 20%, 20%)
  

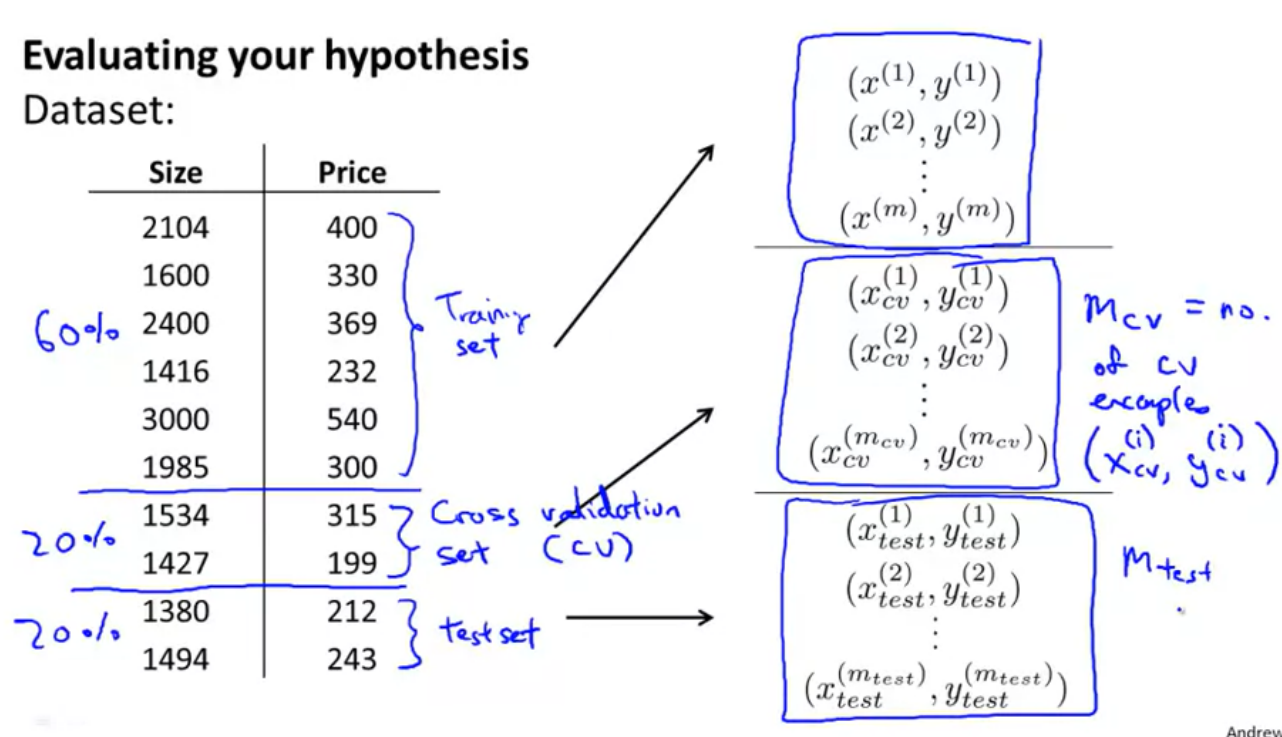
• 아래와 같은 수식으로 표현 가능
  

• Cross Validation이 추가되었으므로
  

  1. Taining set을 통해 θ를 구함
  2. θ와 Cross Validation을 이용해 오차를 구함 -> 가장 낮은 오차를 가지는 가설함수 선택
  3. 선택한 가설함수를 가지고 Test set을 통해 오차를 구함
  4. 구한 값으로 Overfitting인지 underfitting인지 판별

📌 Diagnosing Bias vs. Variance

편향과 분산 진단

• Underfit - High bias / Overfit - High Variance
  

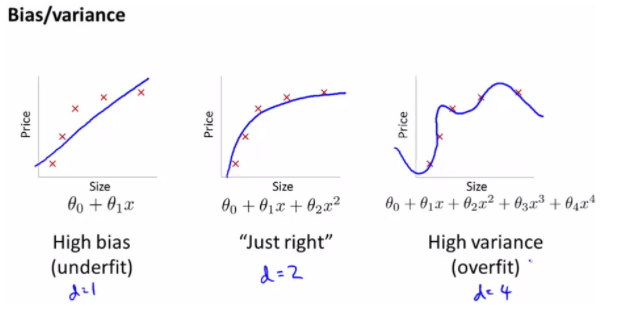
• Bias vs Variance
  
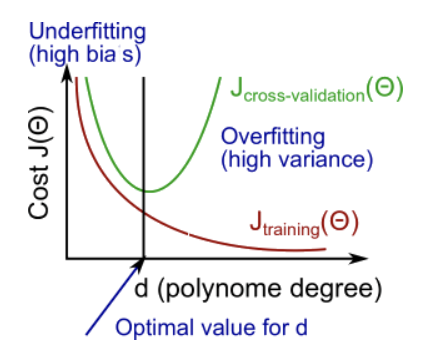
  d가 높아질수록
  training set의 cost function값은 계속 작아짐
  validation set의 cost function값은 작아지다가 어느 순간부터 다시 증가함

  따라서
  Jtrain과 Jvalidation의 값이 모두 큰 경우 - Underfitting
  Jtrain의 값은 작지만 Jvalidation의 값이 큰 경우 - Overfitting

• Bias와 Variance를 구분하는 방법
  
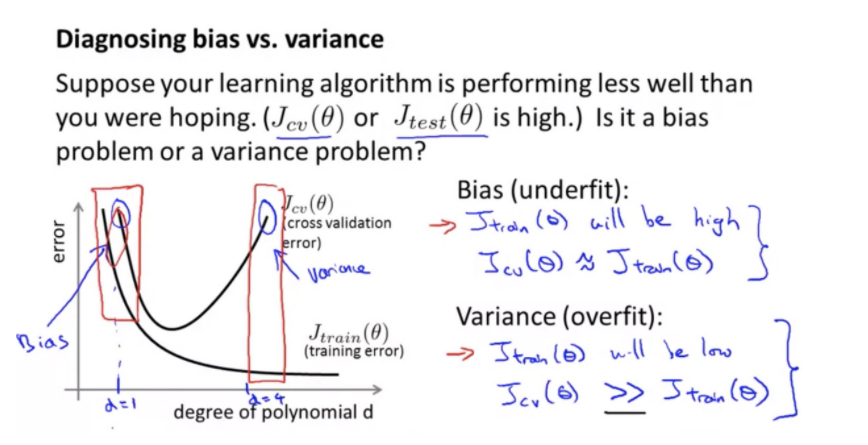
  Cross Validation error와 Training error의 그래프는 대부분 위와 같으므로, Cross Validation error와 Training error의 그래프를 그려 문제를 찾고 적절한 차수를 찾기

📌 Regularization and Bias/Variance

정규화와 편향/분산

• lambda값에 따라 결과가 달리짐
  
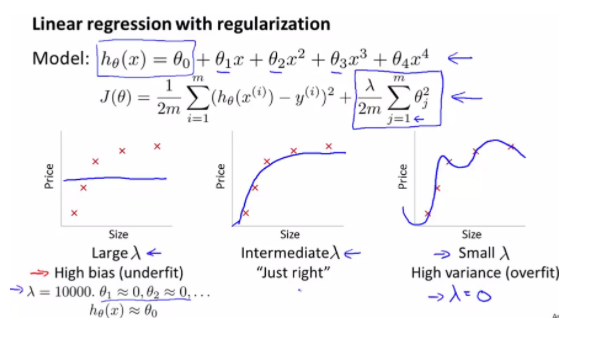
  lambda값이 너무 크면 parameter -> 거의 0에 수렴 -> Underfitting
  lambda값이 너무 작으면 parameter -> test set에 Overfitting

• 적절한 lambda값을 구하는 방법
  
  

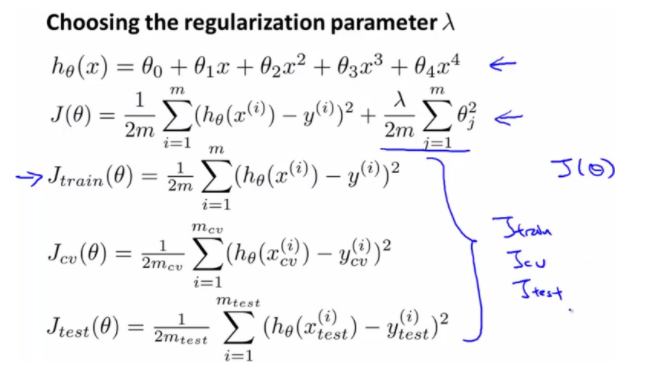
  1. lambda값을 0부터 조금씩 증가시켜가면서 J(θ)에 적용하여 θ값을 구함
  2. 구한 θ를 Cross Validation을 적용하여 error값을 구함
     -> 적절한 lambda값 = 가장 작은 error값을 가지는 lambda값
  3. but, 새로운 Data가 들어오면 적절한 값이라는 보장 X
     -> lambda값을 Test set에 적용하여 error값을 구함

• 적절한 lambda값을 판단하는 방법
  
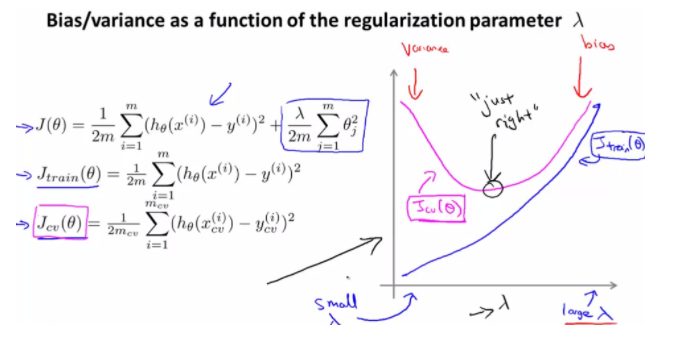
  Training error -> lambda값이 클 수록 커짐
  Cross Validation error -> lambda값이 클수록 작아지다가 일정한 부분에서 커짐

  임의의 lambda를 기준으로, 왼쪽 - Overfitting / 오른쪽 - Underfitting

  Cross Validation error 大 and Training error 大 -> Underfitting
  Cross Validation error 大 and Training error 小 -> Overfitting
  두 그래프가 거의 일치하는 부분 or 두 그래프의 에러가 가장 낮은 부분 -> 가장 적절한 lambda값
  

📌 Learning Curves

학습 곡선

1. High bias
   
   

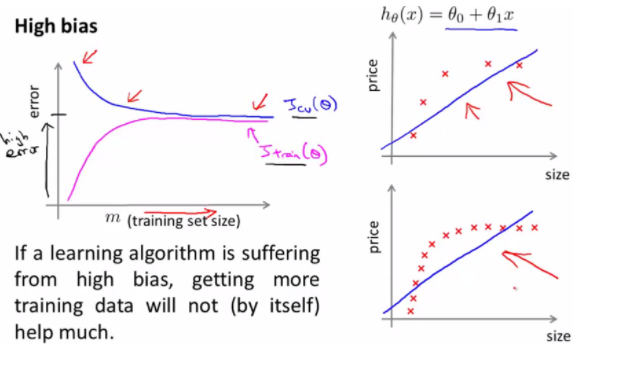
   Training error : 자료가 많아질수록 빠르게 증가하다 일정한 수준에 도달하면 fitting 할 수 있는 한계가 발생하여 일정해짐
   Cross Validation error : 자료가 많아질수록 빠르게 감소하다 일정한 수준에 도달하면 fitting 할 수 있는 한계가 발생하여 일정해짐

   -> 자료를 늘려도 에러가 줄어들지 않음

2. High Variance

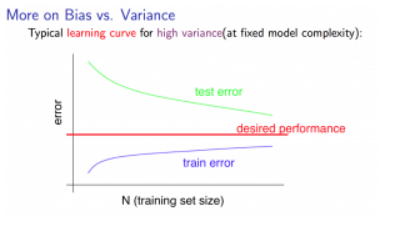
   Training error : 자료가 많아질수록 천천히 증가
   Cross Validation error : 자료가 많아질수록 천천히 감소

   -> 자료를 늘리면 에러가 줄어듦
   

📌 Deciding What to Do Next Revisited

• 가설을 예측한 것에서 오류가 발생한 경우 해결 방법
  

  1. 더 많은 학습 데이터 사용하기 = High Variance
  2. features 줄이기 = High Variance
  3. features 추가하기 = High bias
  4. polynomial(고차원) 항 추가하기 = High bias
  5. lambda값 줄이기 = High bias
  6. lambda값 늘이기 = High Variance

• Neural Network에 적용
  

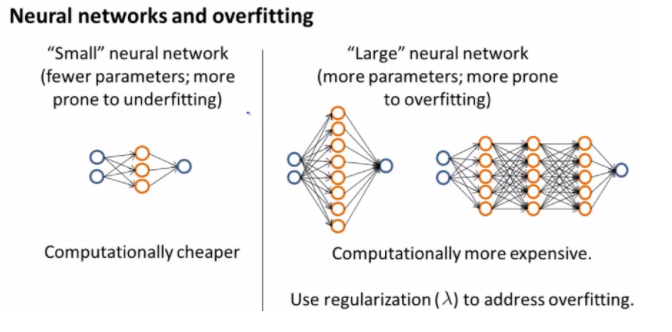
  1. Hidden layer / parameter의 수가 적은 경우
     -> Underfitting(High bias) But, Computing이 빠름
  2. Hidden layer / parameter의 수가 많은 경우
     -> Overfitting(High Variance) But, Computing이 느림

📌 Prioritizing What to Work On

Machine Learning 설계 시 주의 사항

EX) 스팸 분류

왼쪽 : 스팸메일 O / 오른쪽 : 스팸메일 X

스팸메일 -> 의도적으로 단어의 철자를 제대로 사용하지 않음

• 스팸메일 분류 시스템을 설계
  

  1. 이메일이라는 데이터에서 feature x를 정의
     ( feature x = 이메일에서 존재할 수 있는 단어 중 100개를 선택한 것 ) But, 실제로는 단어를 10000 ~ 50000개 정도 선택해야함
  2. feature x와 이에 대한 labeling y가 존재 -> 로지스틱 회귀 이용

• 정확성은 향상시키고 error는 줄이는 방법
  

  1. train data를 많이 모으기
  2. 보다 정교한 feature 만들기
  3. 단어의 존재 유무와 더불어 문맥에 따라 스팸 여부 판별
  4. 의도적인 오타에 대한 알고리즘을 개발
  • But, 실제로 어떤 것이 가장 좋은 방법인지 확정짓기 어렵기 때문에 조금 더 명확한 방법은 나중에 알아보도록 함

📌 Error Analysis

오류 분석

• 접근 방법
  
  1. 간단한 알고리즘부터 시작
  2. Learning Curves를 그려 data와 features 중 더 필요한 것 판별
  3. Error analysis을 통해 오류의 원인을 찾아 수정