
Hypothesis and Cost
-
가설(H(x))함수와 비용(cost)함수
-
simplified hypothesis
: 간단한 표현을 위해 b를 없앤다- cost가 최소화되는 W값을 찾는 것이 Linear Regression의 목표
-> 위의 cost함수를 사용하면 W값을 찾을 수 있다
- cost가 최소화되는 W값을 찾는 것이 Linear Regression의 목표
Gradient descent algorithm (경사하강알고리즘)
: 경사도에 따라 움직임을 반복하다가 경사도가 0이되는 곳에서 멈춘다
-> cost를 최소화시킬 수 있다
-
움직이는 방법 (=작동 방법)
- 어떤 점에서 시작하든 최소점에 도달할 수 있기 때문에 아무 점에서 시작한다
- W를 cost가 줄어드는 방향으로 조금씩 바꾼다
- 2번을 반복하여 cost가 0인 곳을 찾는다
-
경사도 구하는 방법
- 기울기를 구하기 위해 cost함수를 미분한다
- descent algorithm
-> cost function 최소화하는 W를 구할 수 있다
- 기울기를 구하기 위해 cost함수를 미분한다
-
Convex function
- cost function의 모양이 밥그릇처럼 Convex한 모양이라면 안심하고 Gradient descent algorithm을 사용해도 된다
-> 어느지점에서 시작하든지 최소점에 도달하기 때문!
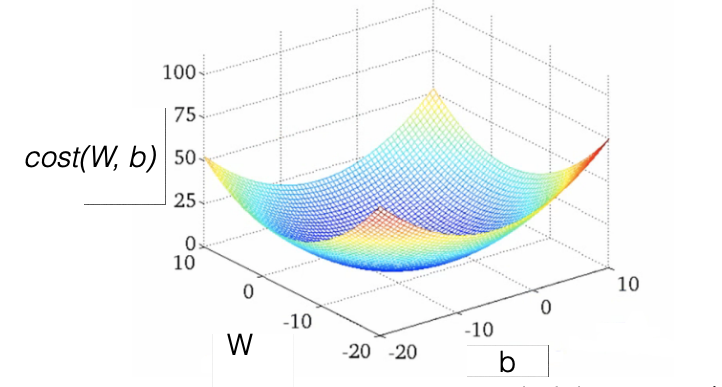
- cost function의 모양이 밥그릇처럼 Convex한 모양이라면 안심하고 Gradient descent algorithm을 사용해도 된다
