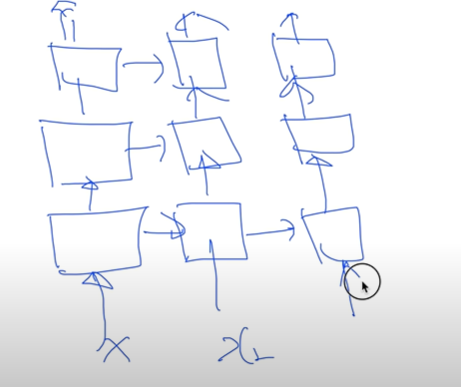
NN for XOR

activation function으로 sigmoid 사용
-> activation function이란, 일정 값 이상이 되면 activation이 되도록 함

Vanishing Gradient

Backpropagation에서 layer 수가 많아지면 문제가 발생,

왜냐하면 Chain-rule과 Sigmoid가 1보다 작은 값을 계속 곱하기 때문에,
오른쪽 입력 값이 계속 작아져 왼쪽 출력 결과에 미치는 영향이 작아짐
(= 왼쪽으로 갈수록 경사도가 점점 사라짐)
(= 학습하기 어려움)

-> 여기서 많은 layer를 이용한다고 하더라도 정확도는 높아지지 않음

=> 이러한 문제를 Vanishing Gradient라 부름

Vanishing Gradient 해결방법

Hinton이 주장한 과거 ML의 문제
1. Our labeled datasets were thousands of times too small.
2. Our computers were millions of times too slow.
3. We initialized the weights in a stupid way.
4. We used the wrong type of non-linearity.

[solution 1] ReLU (Rectified Linear Unit)

"We used the wrong type of non-linearity." => sigmoid 문제

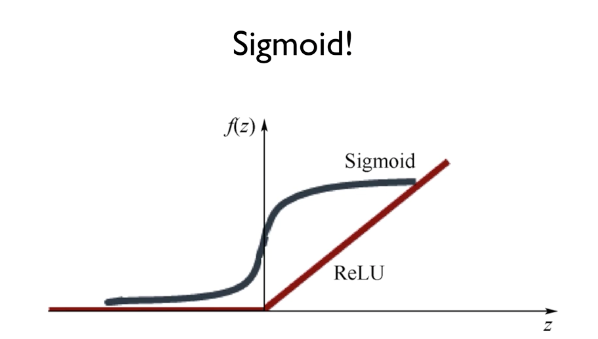
sigmoid 문제점
-> Chain-rule과 Sigmoid가 1보다 작은 값을 계속 곱함

해결방법

Activation function으로 sigmoid 대신에 ReLU 사용
단, 가장 마지막 출력에만 Sigmoid 사용

[solution 2] weight 초기화

"We initialized the weights in a stupid way." => W를 random 값으로 설정했기 때문에 Activation function으로 sigmoid 대신에 ReLU 사용한 코드여도 서로 다른 cost function 그래프를 얻게 됨

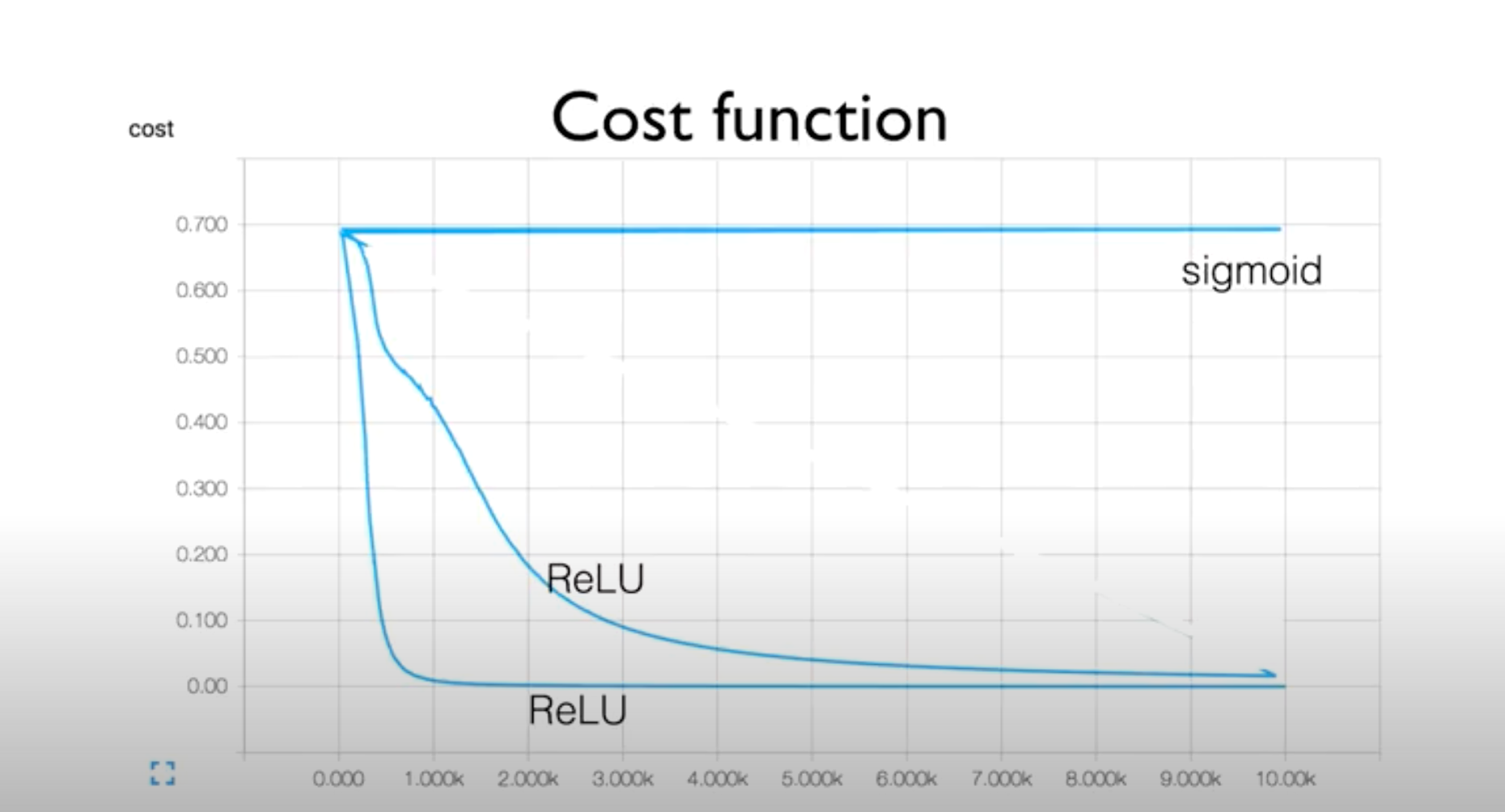
weight 문제점
-> random 값임
-> 여기서 W를 항상 0으로 초기화한다고 하더라도, 미분값도 0이 되기 때문에 gradient가 사라지는 문제가 발생

해결방법

1. RBM(Restricted Boatman Machine) in 2006
   : 레이어 두개가 있을때, encode는 기존의 X라는 데이터셋에 W를 곱해 값을 만들고, decode는 encode의 역방향으로 똑같은 과정을 진행
   -> encode에서 사용한 기존 X와 decode를 통해 새로 얻은 값을 비교해 둘의 차이가 가장 작아지도록 W를 조절하여 초기값과 유사하게 만듦
   But, 너무 복잡

2. Xavier initialization in 2010
   = Glorot Initialization
   : 활성화 함수가 선형인것을 전제로하여 앞 층의 노드가 n개라할 때, 가중치의 초기값이 표준편차가 1/root(n)인 분포를 따르는 랜덤 값을 사용
   But, ReLU 사용시 비효율적

3. He's initialization in 2015
   : 입력값(fan-in)과 출력값(fan-out)의 개수에 비례하게 W를 초기화
   -> 앞 층의 노드가 n개라면 가중치의 초기값은 표준편차가 2/root(n)인 분포를 따르는 랜덤한 값을 사용

---

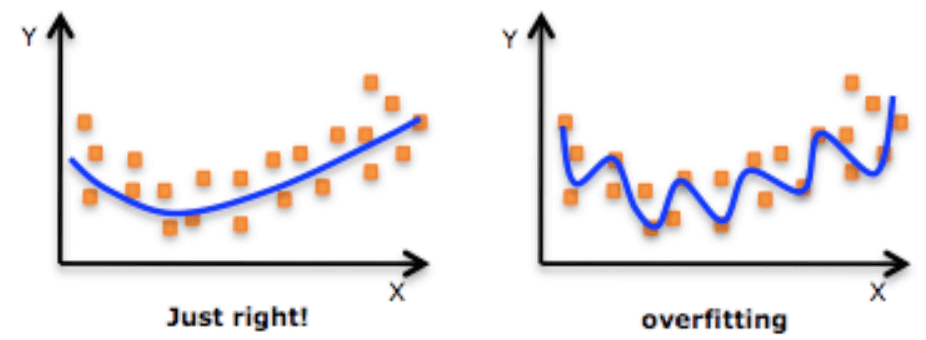
Overfitting(과적합) 문제 해결방법

1. More training data
2. Reduce the number of features
3. Regularization

Regularization

: weight에 너무 큰 가중치를 주자 말자

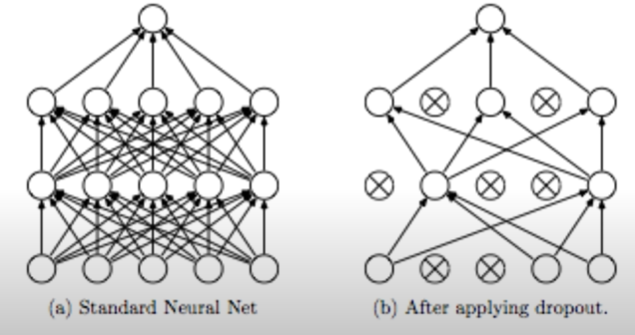
1. Dropout
   : "randomly set some neurons to zero in the forward pass"
   : "랜덤으로 뉴런들을 끊어서 0으로 만들자(=버리자)"
   

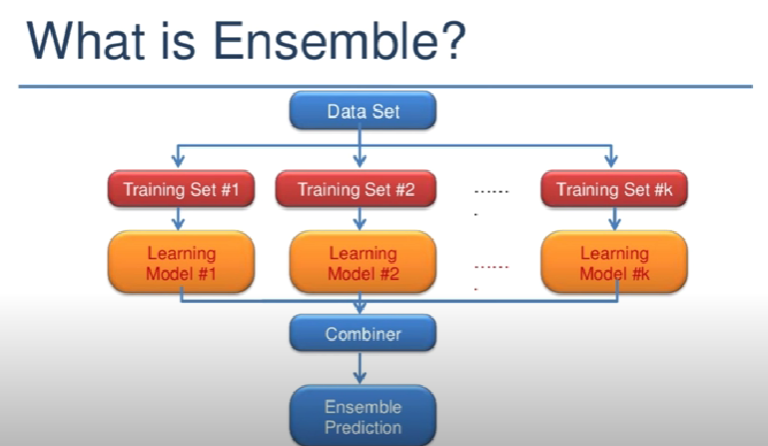
2. Ensenble
   : 똑같은 형태의 독립적인 Neural Network를 만들어 각각을 학습시킨 후, 모델의 결과들을 모두 합쳐 최종 모델을 만듦
   

---

Feedforward neural network (순방향 신경망)

: 레고처럼 neural network를 쌓는 방법
: 인공 신경망 모델 중 가장 기본이 되는 모델

• Fast forward : 중간의 출력을 앞으로 당김
  

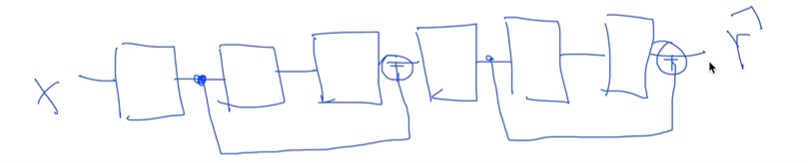
• Split & Merge
  

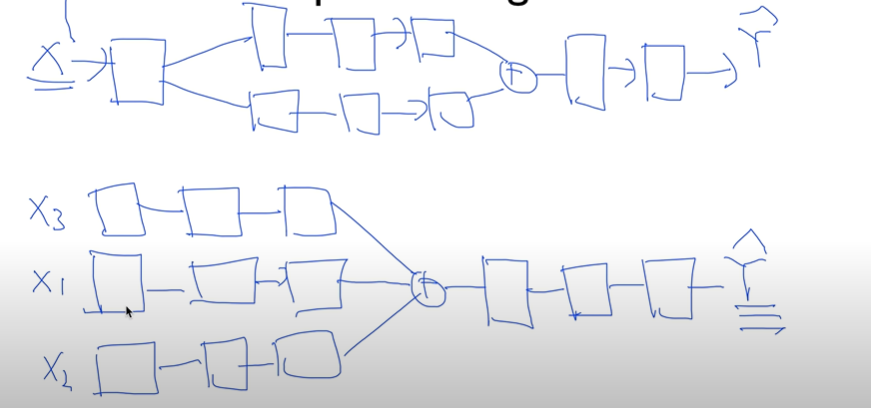
• Recurrent network : 옆으로 나아감
  - output이 다시 input으로 돌아올 수 있음