[CS231N] Lecture 3 Loss Functions and Optimization

Lecture 3에서는 Loss function(손실 함수)와 Optimization(최적화)에 대해 배웠다.
1. Loss Functions

여러 W값 중 어떤 W가 가장 좋은지 알기 위해서는 특정 W값이 양적으로 얼마나 나쁜지 알아야 한다.
Loss function : score(점수)를 이용해 이에 영향을 준 임의의 W를 수량화하여 W가 얼마나 나쁜지 알려주는 함수
훈련 데이터 셋에 X,Y가 있다고 가정하고 손실 함수 구하는 과정을 공식화 해준다.
X : 입력 이미지
Y : 레이블(알고리즘이 예측하기를 원하는 값으로, 각 이미지 X에 대한 올바른 범주가 무엇인지 알려주는 정수)
이때 L(손실) : N개의 데이터 셋을 각각에 대해 f(x_i, W)(= X에 가중치 W를 취해 예측된 score) 와 레이블 y_i(= 해당 이미지 범주가 맞으면 1, 나머지는 0)의 차이들의 평균값
1-1. Multiclass SVM Loss(Hinge Loss)

=> 그래프 상에서 x축은 정답일 때의 점수, y축은 L을 나타낸다. 정답 클래스를 올바르게 분류했다면 L_i가 0에 가까워지고 그렇지 않으면 L이 선형적으로 감소한다.
S : 입력 이미지 x_i와 가중치 W의 함수 ; 분류기를 통해 얻은 예측 점수
S_j : 입력 이미지와 다른 범주의 점수 (오답일 때의 점수)
S_y_i : i번째 입력 이미지와 일치하는 범주의 점수 (정답일 때의 점수)
safty margin = 1 : 예측 값과 정답 사이의 차이를 주기 위해 설정한 여백
L_i = i번째 입력 이미지에 대한 정답 범주를 제외하고 max(0, 나머지 범주의 점수 - 정답 점수 + 1)를 구한 값의 합




Q1. What happens to loss if car scores change a bit?
A1. 여백이 1만큼 유지될 정도로 정답 점수가 다른 오답 점수들보다 상대적으로 높다면 정답 점수가 바뀌더라도 손실 값은 영향을 받지 않고 유지된다.
Q2. What is the min/max possible loss?
A2. min : 0, max : 무한대
Q3. At initialization W is small so all s = 0. What is the Loss?
(초기에 W가 0에 가까우면 모든 score값이 0과 비슷하다. 이때 손실은?)
A3. L = (클래스) - 1이 된다. L을 계산할 때 (정답이 아닌 클래스)를 순회하고 비교하는 두 점수가 거의 비슷해지기 때문에 L은 (클래스의 개수) - 1이 된다.
Q4. What if the sum was over all classes? (including j = y_j)
(L_i를 구할 때, j를 포함하는 모든 값을 다 더하게 되면 어떻게 되는가?)
A4. 입력 이미지와 분류된 범주가 일치할 때(정답일 때), L_i = 1이 나오기 때문에 기존 L_i 값에 + 1만큼 추가한 값이 될 것이다.
Q5. What if we used mean instead of sum?
(L을 구할 때 합 대신 평균을 사용한다면 어떻게 되는가?)
A5. L 값에는 변화가 없다.
Q6. What if we used squared hinge loss [ max(0, (S_j - S_y_i) ^ 2) ] ?
A6. 손실 함수 계산식이 바뀐 것이기 때문에 L이 완전히 달라진다.
+) squared hinge loss를 사용하는 경우 : 오류를 더 명확하게 보이게 함으로써 정확도가 더 높은 모델을 만들기 위해 (제곱을 하게 되면 오차값이 상대적으로 더 커지면서 Loss가 더 커지고 정확도가 낮아 보임)
Regulation
Q. Loss = 0을 만족하는 W가 하나뿐인가?
A. W는 유일하지 않다.



=> Regulation를 통해 가장 좋은 W 값을 찾는다.
Regulation : 손실 함수에 추가 항(람다 * R(W)) regulation loss를 더해 학습데이터와 테스트 데이터 모두에서 성능이 좋아지게 하는 W를 구하는 방식으로, supervised learning(지도 학습) 방식과 비슷하다.
-
L2 regulation : 가중치 W의 유클리드 Norm에 추가 항을 더 함
상대적으로 W1과 W2 중 어느 것이 더 거친지 측정하는 방식으로 분류기의 복잡성을 결정함 -> X의 모든 값에 영향을 분산하는 것을 선호한다. -
L1 regulation : 가중치 W의 0의 개수에 따라 모델의 복잡도를 결정함
1-2) Softmax


- SVM vs. Softmax
SVM : 정답 점수와 오답 점수간의 여백에만 신경 쓴다. (= 둔감함)
Softmax : 모든 단일 데이터를 지속적으로 개선하여 성능을 더 높이려고 하기 때문에 정답 클래스의 점수는 무한대로, 나머지 클래스의 점수는 -무한대로 가게 된다. (= 예민함)
 step1) 고양이 이미지가 입력되었을 때 각 클래스의 점수를 가져온다.
step1) 고양이 이미지가 입력되었을 때 각 클래스의 점수를 가져온다.
step2) 모든 점수가 양수가 되도록 지수화 해준다.
step3) step2의 모든 값을 정규화(normalize)해준다.
=> L = step3에서 구한 실제 클래스 점수(확률)의 음의 로그 : -log(정답 클래스의 확률)
이 때 Loss는 badness를 측정하는 것이기 때문에 -1을 곱해 음의 값을 얻는다.Q1. What is the min/max possible Loss L_i?
A1. min = 0, max = 무한대
Q2. Usually at initialization W is small as all s = 0. What is the loss?
A2. L = -log1/C = logC
2. Optimization
optimizatin : 최적화, L = 0인 W를 찾는 방법
방법 1. Random Search
: W를 무작위로 샘플링하여 손실 함수에 넣고 성능이 얼마나 좋은지 확인한다. 항상 좋은 위치를 찾을 보장이 없기 때문에 사용하지 않는다.
방법 2. Gradient Descent
: 경사 하강법, 기울기나 도함수 값을 통해 loss를 파악한다.
 gradient > 0이면 Loss는 증가한 것이고, gradient = 0이면 Loss가 동일한 것이다.
gradient > 0이면 Loss는 증가한 것이고, gradient = 0이면 Loss가 동일한 것이다.

모든 데이터에 대해 작업할 때 연산량을 줄이기 위해 minibatch(묶음)를 이용하는데 이 방법을 Stochastic Gradient Descent(SGD)라고 한다. 일부분을 사용해 gradient를 계산한다.
+) Backpropagation을 하면서 다시 값을 계산해주기 때문에 초반에 SGD 방식으로 초기화 해줘도 괜찮다.
Image Features
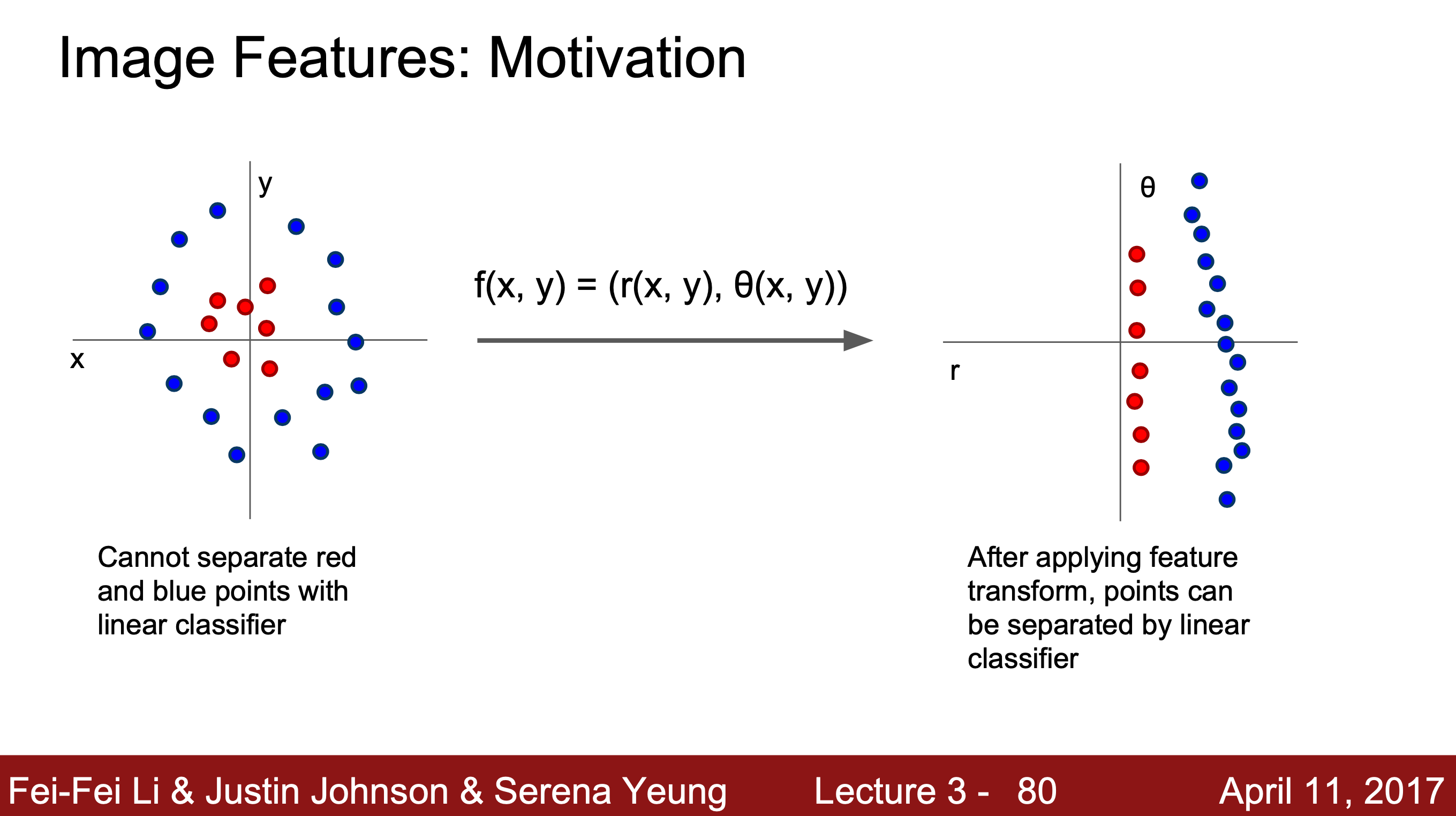
Q. 왼쪽을 오른쪽 그림과 같이 분류 가능하게 만들려면 어떤 변환을 해야 할까?
1. color histogram
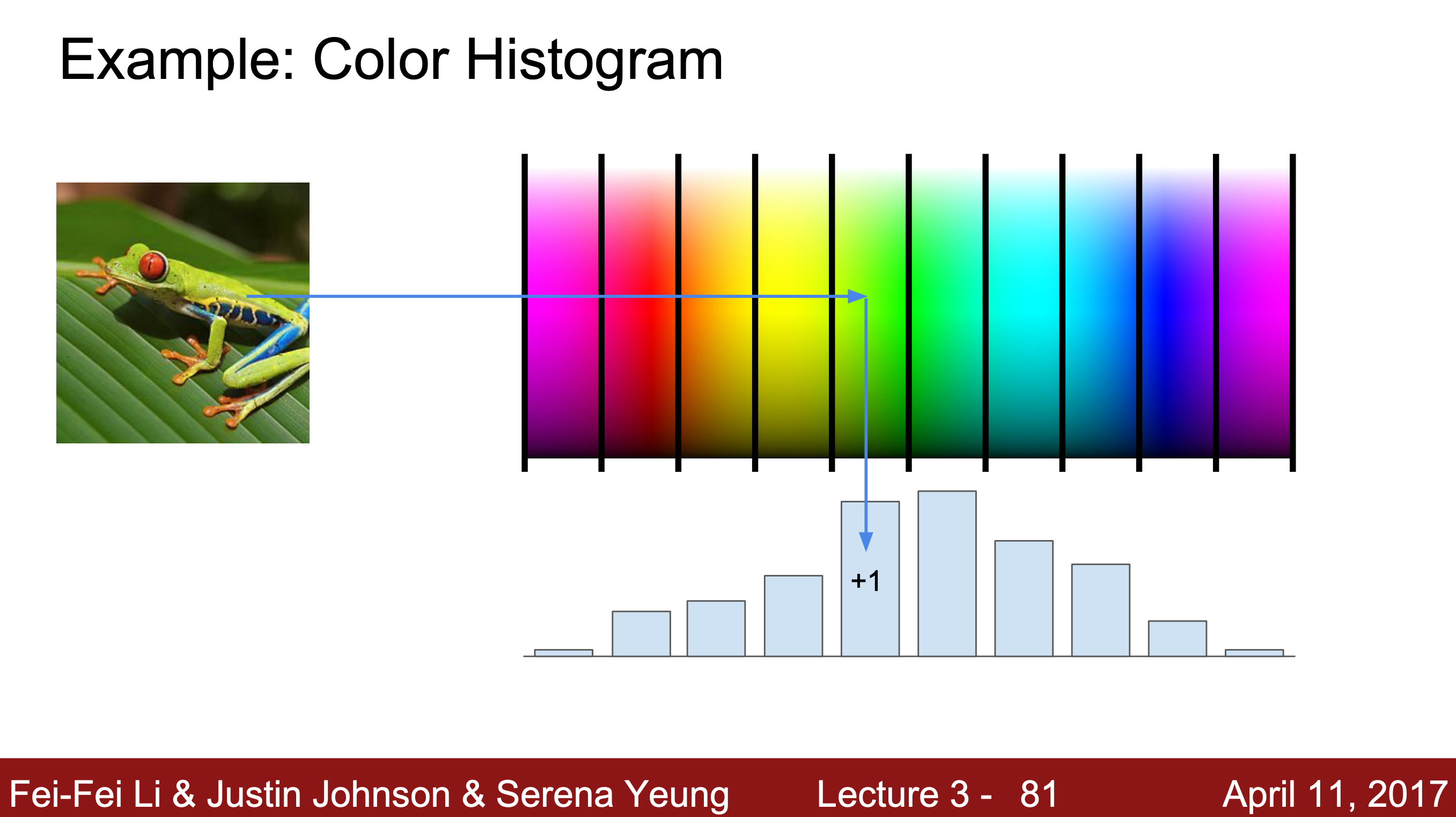 : 이미지의 전체적인 색깔을 나타낸다.
: 이미지의 전체적인 색깔을 나타낸다.
2. Histogram of Oriented Gradients (HoG)
 : 이미지에 전반적인 모서리 정보를 나타낸다.
: 이미지에 전반적인 모서리 정보를 나타낸다.
3. Bag of Words 
+) 1, 2, 3의 방법들이 전통적인 머신러닝 방식이라면, CNN은 학습을 하면서 데이터의 특징을 자동으로 찾아낼 수 있다는 차이점이 있다.
