- 코드잇 강의 바로 가기

다항 회귀

01. 다항 회귀 (Polynomial Regression)

• 다항 회귀(polynomial regression) : 데이터에 잘 맞는 다항식이나 곡선을 구해서 학습하는 알고리즘

  선형 회귀에서는 데이터에 가장 잘 맞는 "직선"을 찾았는데 입력 변수와 목표 변수의 관계를 가장 잘 나타내는 게 직선이 아닐 수도 있다.
  이러한 문제를 개선하기 위해서는 직선이 아닌 "곡선"을 사용할 수 있다.

  기존 선형 회귀에서의 가설 함수가 $h_\theta(x) = θ_0 + θ_1x$ 이므로 이 가설 함수를 곡선으로 바꿔주면 된다.
  만약 데이터에 가장 잘 맞는 곡선이 이차 함수일 것 같으면,
  $h_\theta(x) = θ_0 + θ_1x + θ_2x^2$,
  만약 데이터에 가장 잘 맞는 곡선이 삼차 함수일 것 같으면,
  $h_\theta(x) = θ_0 + θ_1x + θ_2x^2 + θ_3x^3$와 같은 가설 함수를 사용하면 된다.

  함수의 차수가 더 높을수록 그래프 상에서 굴곡이 더 많은 곡선으로, 데이터를 보고 적합할 것 같은 가설 함수의 모양을 고르면 된다.
  
  

  1. 단일 속성 다항 회귀

  : 속성이 하나인 다항 회귀
  ex) 집 크기를 이용해서 집 가격을 예측하는 경우

  만약 가설 함수가 이차 함수인 다항 회귀를 한다면,
  $h_\theta(x) = θ_0 + θ_1x + θ_2x^2$에서 학습 데이터에 가장 잘 맞는 $\theta_0$, $\theta_1$, $\theta_2$를 찾으면 되고
  만약 가설 함수가 삼차 함수인 다항 회귀를 한다면,
  $h_\theta(x) = θ_0 + θ_1x + θ_2x^2 + θ_3x^3$에서 학습 데이터에 가장 잘 맞는 $\theta_0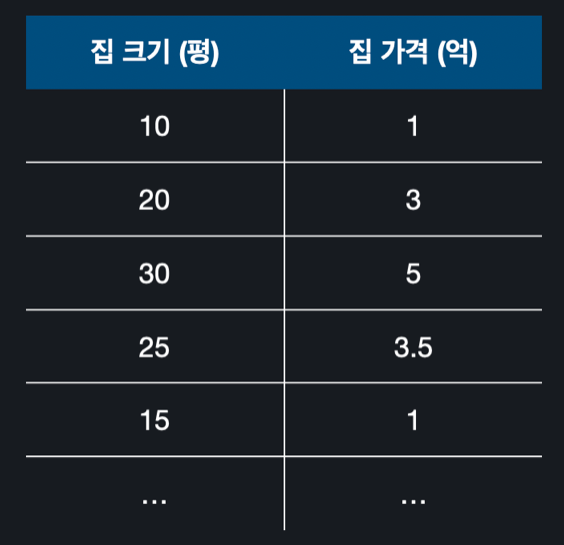$, $\theta_1$, $\theta_2$, $\theta_3$를 찾으면 된다.위와 같은 데이터가 있을 때, 집 크기를 제곱한 값과 세제곱한 값을 넣어 가상의 열 두 개를 추가한다.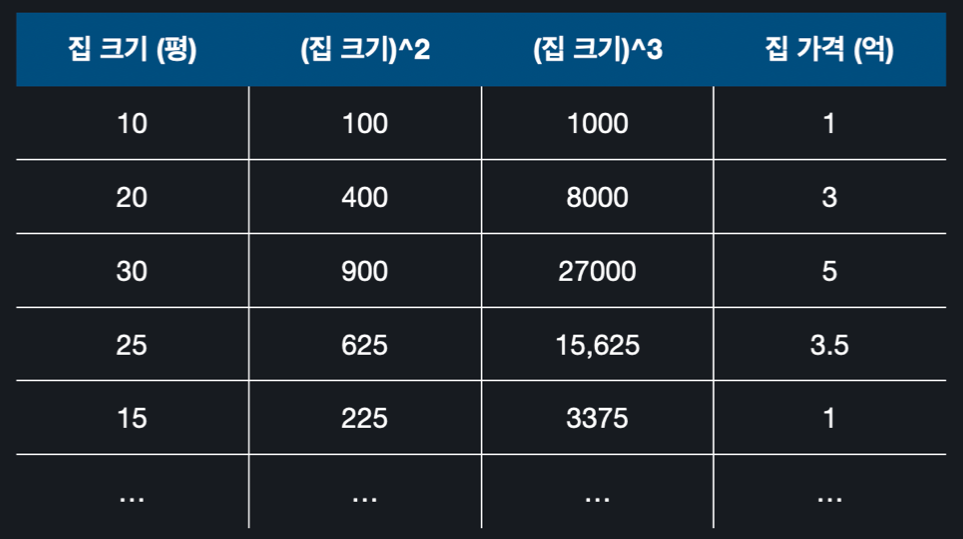위와 같은 데이터를 가지고 입력 변수 $x^1$, $x^2$, $x^3$를 선형 회귀에서의 $x_1$, $x_2$, $x_3$처럼 취급해 다중 선형 회귀를 하면 된다.

  2. 다중 다항 회귀

  : 속성이 여러 개인 다항 회귀
  ex) 집 크기, 방 수, 지하철까지의 거리를 이용해서 집 가격을 예측하는 경우

  집 크기를 $x_1$, 방 수를 $x_2$, 지하철까지의 거리를 $x_3$로 입력 변수를 설정해준다.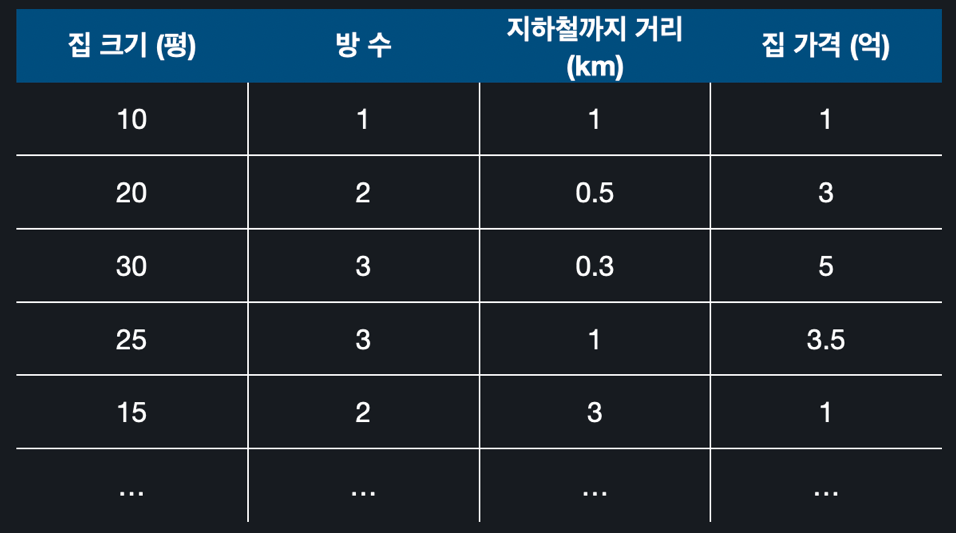만약 가설 함수가 이차 함수인 경우라면, 제일 큰 항이 이차항이고 입력 변수로 만들 수 있는 이차항은 $x_1$$x_2$, $x_2$$x_3$, $x_3$$x_1$, $x_1^2$, $x_2^2$, $x_3^2$총 6개이다.

  이 6가지에 대해 가상의 열을 추가하면 다음과 같다.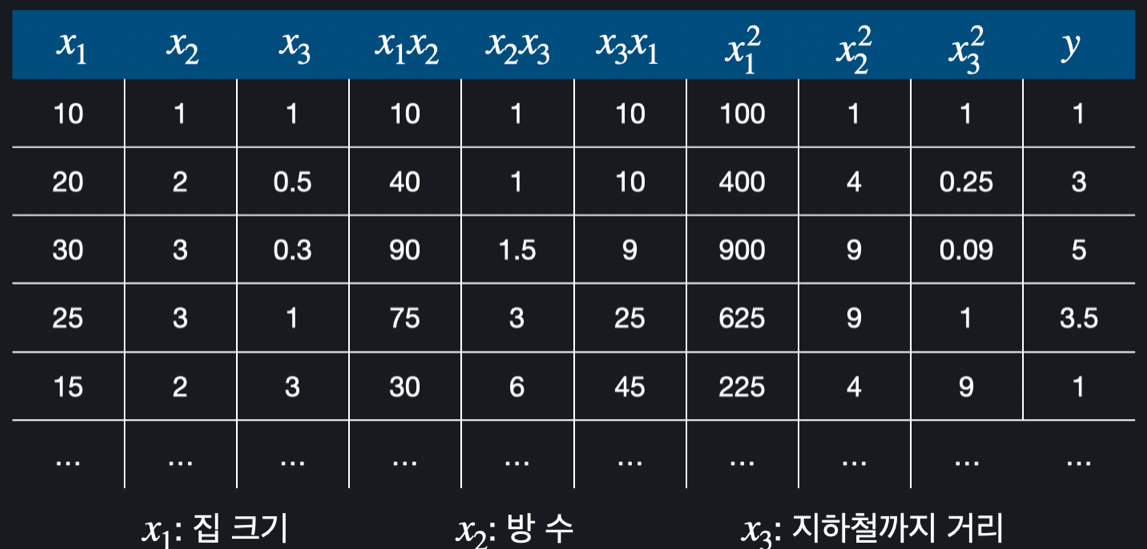이 때 가설 함수는 $h_θ(x) = θ_0 + θ_1x_1 + θ_2x_2 + θ_3x_3 + θ_4x_1x_2 + θ_5x_1x_3 + θ_6x_2x_3 + θ_7x_1^2 + θ_8x_2^2 + θ_9x_3^2$으로 나타난다.
  이 함수를 입력 변수가 9개인 다중 선형 회귀로 취급하고 풀면 된다.

02. 다항 회귀의 힘

집의 너비와 높이 데이터를 통해서 집 가격을 예측한다고 하면, 단순 선형 회귀에서는 두 변수가 서로 독립적이기 때문에 프로그램은 "높이와 너비가 같이 커야지만 집 값도 커진다"라는 관계를 학습할 수 없다. 대신 높이가 집 값에 미치는 영향, 너비가 집 값에 미치는 영향을 따로 찾아내게 된다.

이처럼 단순 선형 회귀는 각각의 속성이 모두 독립적이기 때문에 변수들 사이의 관계를 최종 예측 결과에 반영하지 못한다. 따라서 속성들을 서로 곱해 차항을 높여주면(선형 회귀 문제를 다항 회귀로 만들어주면) 속성들 사이의 있을 수 있는 복잡한 관계들을 학습시킬 수 있게 된다.

03. 다중 선형 회귀 vs. 다항 회귀

• 다중 선형 회귀(Multiple Linear Regression)
  속성이 여러 개인 선형회귀 방법(다중의 독립 변수가 있는 형태)으로, 이때 속성들은 서로 독립적이다.

• 다항회귀(Polynomial Regression)
  데이터에 가장 잘 맞는 최적선이 곡선인 경우(독립 변수의 차수를 높이는 형태)
  다항 회귀에서의 '항'은 차수를 나타내는데 말그대로 '차수가 많다'는 뜻으로, 하나의 속성에 차수를 부여해 여러 특징을 만들어낸다.