- 코드잇 강의 바로 가기

로지스틱 회귀

01. 분류 문제

그동안은 머신 러닝 > 지도 학습 > 회귀(연속적인 값을 예측)에 대한 내용이었다면, 로지스틱 회귀는 분류(정해진 몇 개의 값 중 예측) 문제를 해결한다.
ex) 공부 시간을 통해 시험 통과 여부를 분류하는 상황

02. 로지스틱 회귀(Logistic Regression)

• 로지스틱 회귀 : 데이터에 가장 잘 맞는 "시그모이드 함수"를 찾는 방식
  cf> 선형 회귀 : 데이터에 가장 잘 맞는 "직선"을 찾는 방식
  

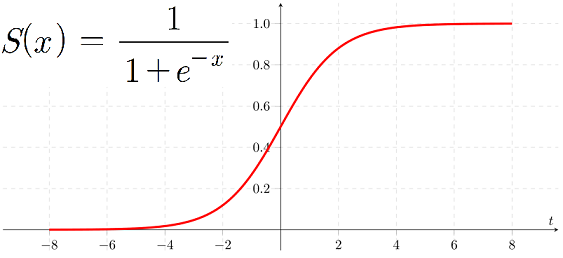
  • 시그모이드 함수 : $S(x) = \frac{1}{1 + e^{-x}}$
    시그모이드 함수는 무조건 0과 1 사이의 결과는 낸다는 특징이 있다.
    x가 엄청 커서 무한대라 하면,
    $S(∞) = \frac{1}{1 + e^{-∞}} = \frac{1}{1 + 0} = 1$
    x가 엄청 작아서 마이너스 무한대라 하면,
    $S(-∞) = \frac{1}{1 + e^{∞}} = \frac{1}{1 + ∞} = 0$로,
    결과적으로 x가 엄청나게 작으면 작으면 시그모이드 함수 값이 0에 가까워지고, x가 엄청나게 크면 1에 가까워진다.

    시그모이드 함수의 결과값이 0 ~ 1 사이의 연속적인 값이기 때문에 로지스틱 "회귀"라고 부르지만 주로 결과값이 0.5보다 큰지 작은지를 보고 분류하기 때문에 이름은 회귀지만 분류에 주로 사용한다.

• 선형 회귀와 로지스틱 회귀

  • 선형 회귀를 이용한 분류
    선형 회귀로도 분류를 할 수 있긴 하다.
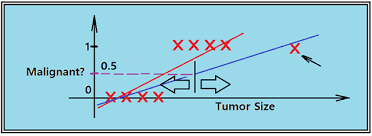    1. 예외적인 하나의 데이터에도 가설 함수가 너무 민감하게 반응한다.
    2. 가설 함수로 일차 함수를 사용하는데, 일차 함수는 결과가 얼마든지 끝없이 작아지거나 커질 수 있다.

  하지만 위와 같은 단점 때문에 분류 문제에서는 선형 회귀를 잘 사용하지 않는다.
  
  

  • 로지스틱 회귀를 이용한 분류
    시그모이드 함수는 결과가 항상 0과 1 사이에 떨어지기 때문에 많이 동떨어진 데이터가 하나 발생하더라도 크게 영향을 받지 않는다.
    
    

03. 로지스틱 회귀 가설 함수

• 가설 함수
  선형 회귀의 가설 함수를 $g_{\theta}(x) = \theta^Tx$라 하면,
  로지스틱 회귀의 가설 함수는 $h_\theta(x) = \frac{1}{1 + e^-g_\theta(x)}$ 이고, $g_{\theta}(x)$ 대신 $\theta^Tx$를 대입해서 쓸 수 있다.
  $g_{\theta}(x)$는 일차 함수로, 값이 엄청나게 커지거나 작아질 수 있지만 시그모이드 함수 $h_\theta(x)$는 항상 0과 1 사이의 결과값만을 갖는다.
  따라서 선형 회귀에서 썼던 가설 함수 $g$의 아웃풋을 시그모이드 함수의 인풋으로 넣어 0과 1 사이의 값이 나오게 만들어 로지스틱 회귀를 할 수 있다.
  
  

• 가설 함수의 아웃풋
  공부한 시간을 바탕으로 시험 통과 여부를 예측한다고 할 때, 0은 '통과 못함' / 1은 '통과함'을 의미한다.
  만약 공부 시간 $x$를 가설 함수에 넣었더니 아웃풋이 0.9가 나왔다면, 이는 목표 변수가 1일 확률이 90%라는 의미이고 50%의 확률을 넘었으니 시험을 통과한다고 분류를 할 수 있다.
  만약 아웃풋이 0.4가 나왔다면, 시험에 통과할 확률이 40%라는 의미이고 통과하지 못한다고 분류된다.
  
  

• 로지스틱 회귀에서 하려는 것
  로지스틱 회귀의 최종 목표는 $\theta$값들을 조율해 주어진 데이터에 가장 잘 맞는 시그모이드 모양의 곡선을 찾아내는 것이다.

  입력 변수가 하나인 경우를 생각해보면, $\theta$가 $\theta_0$, $\theta_1$ 2개가 있다는 것이고 가설 함수는 아래와 같다.
  

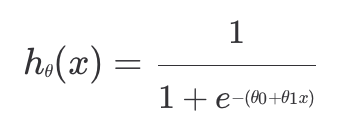
  • $\theta_0$을 늘리면 곡선이 왼쪽으로 움직이고, 줄이면 오른쪽으로 움직인다.
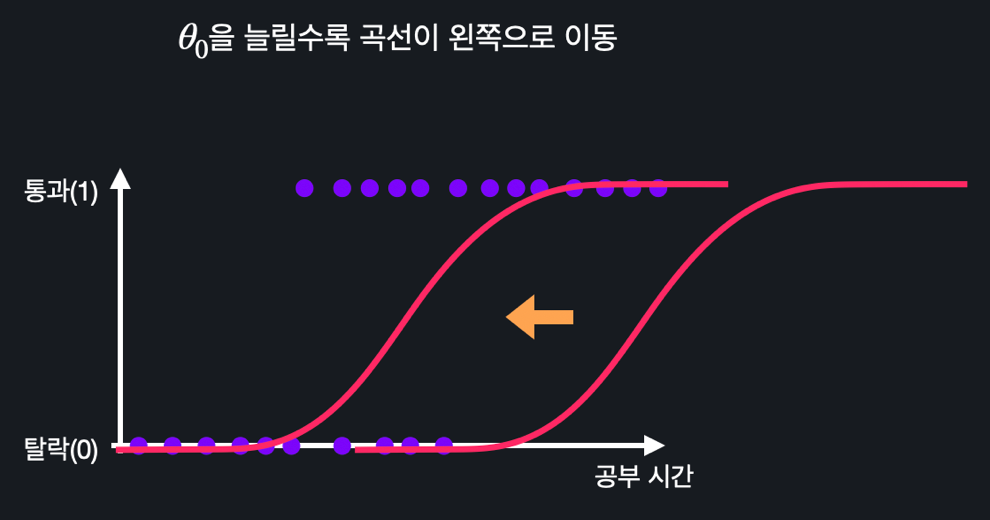
  • $\theta_1$을 늘리면 S 모양 곡선이 직선에 가깝게 가파르게 변하고, 줄이면 완만해진다.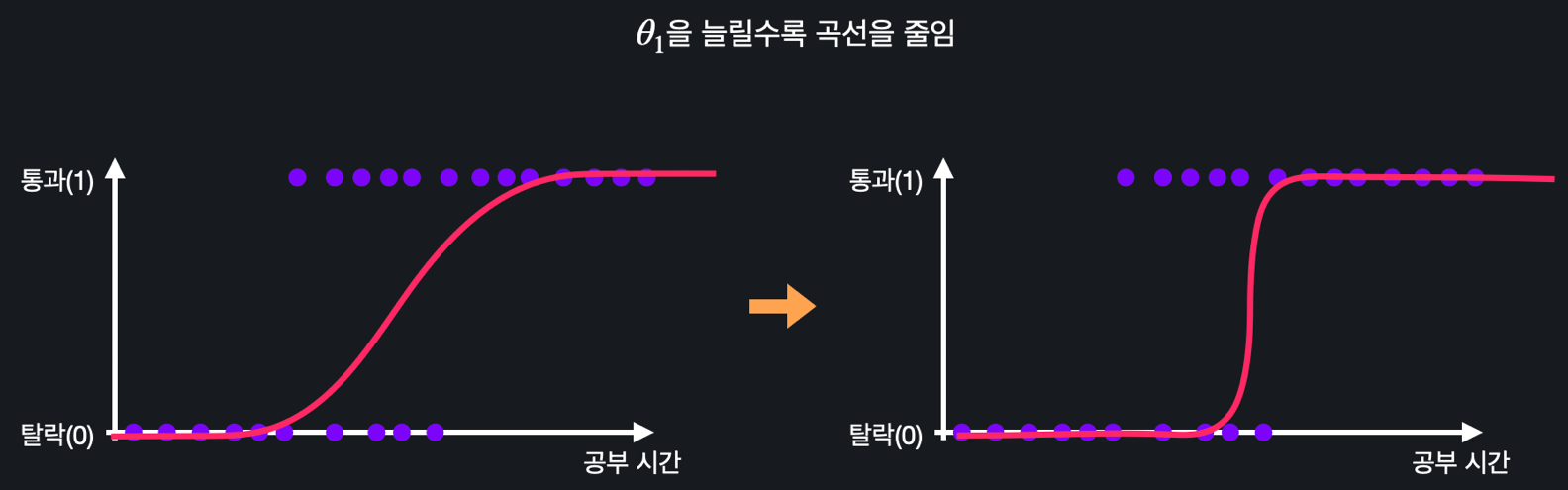이렇게 $\theta_0$, $\theta_1$값들을 바꿔가면서 학습 데이터에 가장 잘 맞는 시그모이드 모양의 곡선을 찾아내면 된다.

  입력 변수가 여러 개인 경우에도 시각화하기는 어렵지만 위와 같은 방식으로 이해하면 된다.
  
  

• 결정 경계(Decision Boundary) : 데이터를 분류하는 결정 경계선

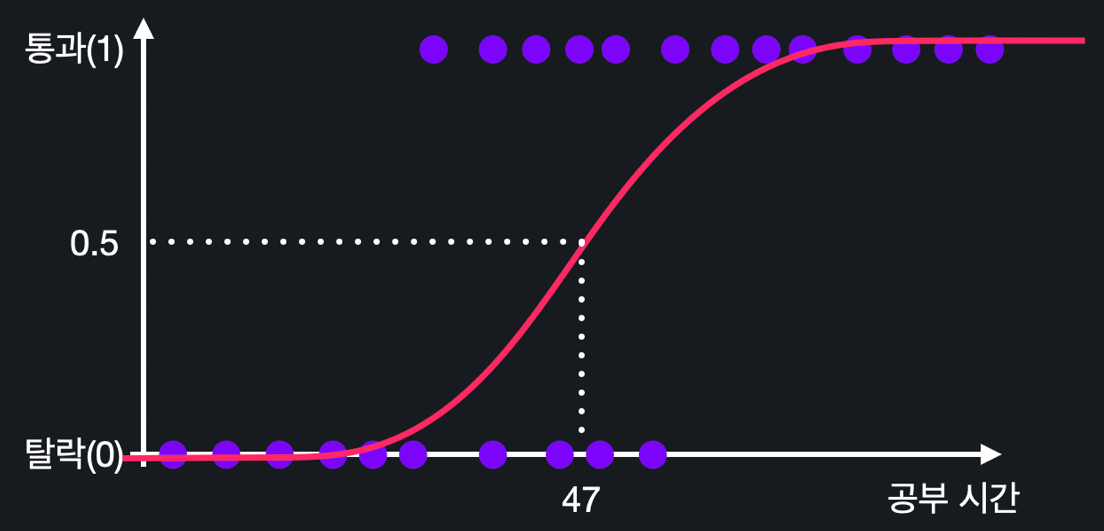
  예를 들어, 0.5를 기준으로 시험 통과 여부를 분류하기 때문에 가설 함수의 아웃풋이 0.5가 되는 x가 47이라고 한다면, 47처럼 분류를 구분하는 경계선을 '결정 경계'라고 한다.

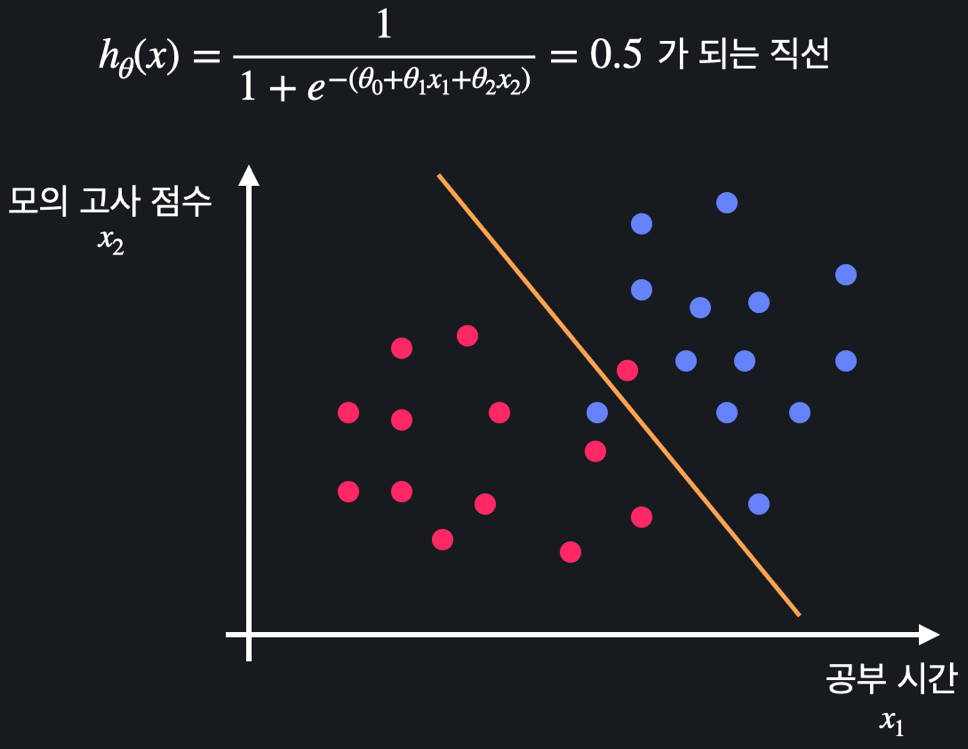
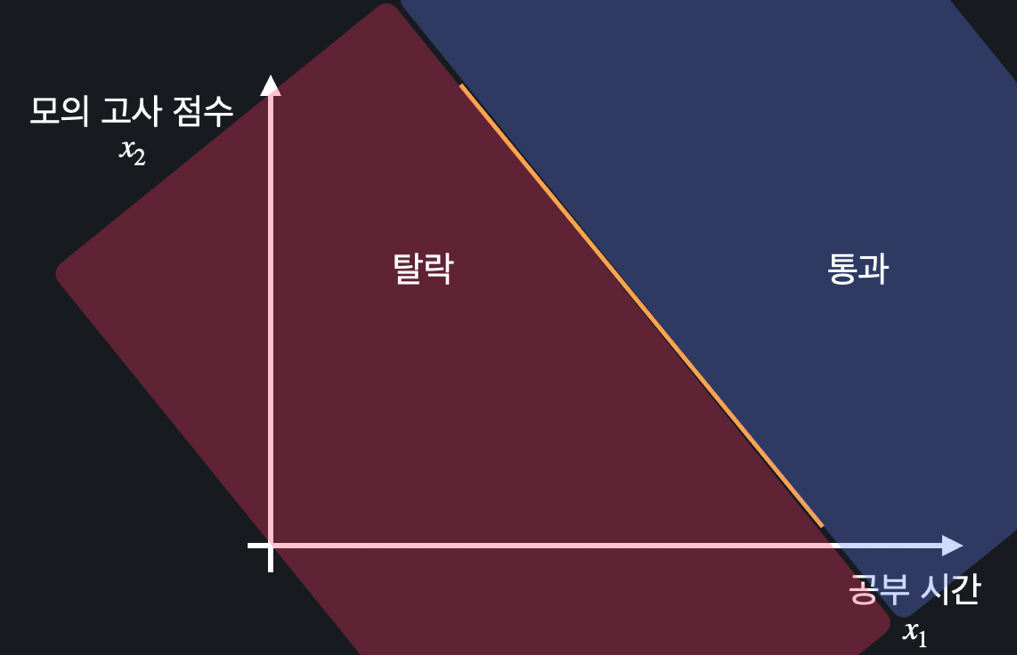
  속성이 2개인 경우, 가설 함수 $h_\theta(x) = 0.5$를 풀어 $x_2 = -2x_1 + 100$과 같이 변수 $x_1$과 $x_2$ 사이의 관계식을 구해 결정 경계로 사용할 수 있다.
  

04. 로그 손실(log loss, cross entropy)

선형 회귀에서 가설 함수를 평가하는 기준인 손실 함수는 평균 제곱 오차(MSE)를 기반으로 했다.
로지스틱 회귀에서는 MSE 대신 '로그 손실'을 사용하여 손실 함수를 만든다.

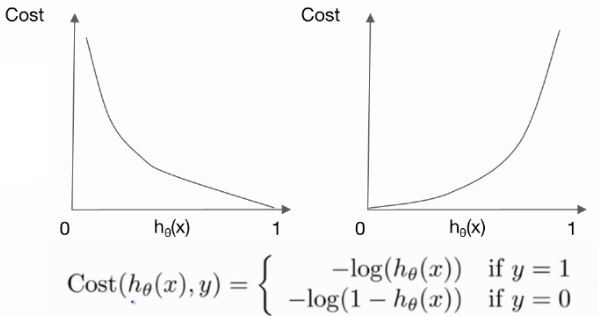
• 로그 손실
  손실의 정도를 로그 함수로 결정하기 때문에 '로그 손실'이라 부른다.
• 로그 손실 함수의 역할
  예측값 $h(x)$가 실제 결과 $y$와 얼마나 괴리가 있는지 알려준다.
  • $y = 1$ 인 경우
    $h(x) = 1$이라면 100% 확률로 아웃풋이 1일 거라 예측한 것이기 때문에 가설 함수와 실제 값이 정확하게 맞아 손실은 0이 된다.
    $h(x)$ 값이 1에서 멀어질수록 실제 결과와 차이가 커지는 것이기 때문에 손실이 점점 커져 급격하게 가파라진다.
  • $y = 0$ 인 경우
    위의 경우와 그래프 모양이 반대로 나타난다.
    $h(x) = 0$이라면 0% 확률로 아웃풋이 1일 거라 예측한 것이기 때문에 가설 함수와 실제 값이 정확하게 맞아 손실은 0이 된다.
    $h(x)$ 값이 0에서 멀어질수록 실제 결과와 차이가 커지는 것이기 때문에 손실이 점점 커져 급격하게 가파라진다.
    
    

05. 로지스틱 회귀 손실 함수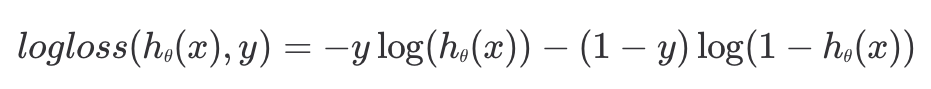

보통 로지스틱 회귀에서 로그 손실은 위와 같은 형태로 표현한다. 목표 변수 $y$는 항상 0 또는 1 둘 중 하나이기 때문에 기존의 식과 완전히 동일한 값을 갖는다.

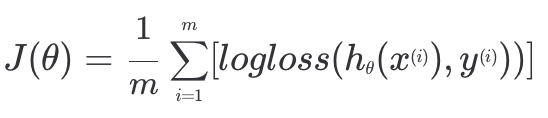
• 로지스틱 회귀 손실 함수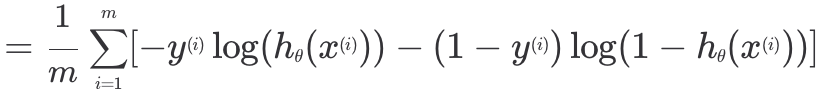각 데이터에 대해 손실을 구한 후, 평균을 내면 된다. 이때 가설 함수의 인풋이 $\theta$였기 때문에 마찬가지로 손실 함수의 인풋도 $\theta$이다.

06. 로지스틱 회귀 경사 하강법

경사 하강법은 선형 회귀와 거의 동일하다.
step 1. 처음 $\theta$값을 모두 0으로 지정하거나 랜덤하게 지정해 경사 하강을 시작한다.
step 2. 현재 $\theta$값들에 대한 손실(가설 함수에 대한 손실)을 계산한다.
step 3. $\theta$를 조율하면서 손실을 계속 줄여나간다.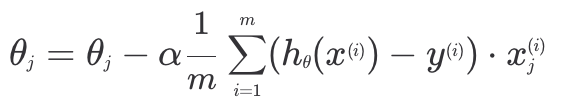손실 함수 $J$를 편미분하면 위와 같은 형태가 나오고, $j$에 $0$ ~ $n$을 넣어 $\theta_0$ ~ $\theta_n$을 업데이트 해주면 된다.

입력변수, 파라미터, 예측값 오차를 행렬과 벡터를 사용해 표현하면 경사 하강 계산 과정을 쉽게 표현할 수 있다.

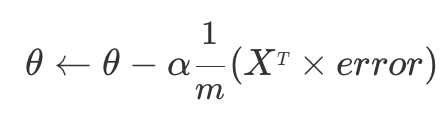
07. 분류가 3개 이상인 경우

그동안은 목표 변수가 0 또는 1, 두 가지 옵션으로만 분류되는 경우에 대해 다뤄보았다.
만약 3가지 옵션으로 분류하고 싶다면 각 0,1,2라는 숫자를 붙여 똑같은 방식으로 분류를 진행하면 된다.

• 전략
  각 옵션별로 단순화하여 문제를 해결하고 결과를 합쳐주면 된다.
  step1. 옵션 0에 대해 0 또는 1의 결과로 분류한다. 이때 옵션 0에 대해 학습시켜 구한 가설 함수를 $h_\theta^{(0)}(x)$이라 한다.
  step2. 옵션 1에 대해 0 또는 1의 결과로 분류하고 $h_\theta^{(1)}(x)$을 구한다.
  step3. 옵션 2에 대해 0 또는 1의 결과로 분류하고 $h_\theta^{(2)}(x)$를 구한다.
  step4. 구한 3개의 가설 함수의 아웃풋 중 가장 값이 큰 옵션으로 분류한다.

  ex) 메일을 직장(0) / 친구(1) / 스팸(2)로 분류할 때, 데이터를 넣어서
  $h_\theta^{(0)}(x) = 0.6$, $h_\theta^{(1)}(x) = 0.45$, $h_\theta^{(2)}(x) = 0.78$이 나왔다면 스팸(2)일 확률이 78%로 가장 높기 때문에 해당 데이터를 스팸 메일로 분류한다.
  
  

08. 로지스틱 회귀와 정규 방정식

선형 회귀에서는 정규 방정식 $\theta = (X^TX)^{-1}X^Ty$ 을 통해 단순 행렬 계산만으로도 최적의 $\theta$값들을 구할 수 있었다. 하지만 로지스틱 회귀에서는 정규 방정식과 같은 단순 행렬 연산만으로는 손실 함수의 최소 지점을 찾을 수 없다.

선형 회귀는 손실 함수 $J(MSE)$가 항상 아래로 볼록한 convex 함수였고 편미분 원소들을 모두 선형식으로 나타낼 수 있었다. 로지스틱 회귀 역시 손실 함수 $J(log loss)$가 아래로 볼록한 형태이기 때문에 경사 하강법을 사용하면 항상 최적의 $\theta$를 찾을 수 있다.
하지만 $\theta$가 e의 지수로 포함되는 가설 함수의 형태 때문에 $J$에 대한 편미분 원소들이 일차식으로만 표현할 수 없게 된다. 따라서 단순 행렬 연산만으로는 최소 지점을 찾아낼 수 없다.