- 코드잇 강의 바로 가기

데이터 전처리

01. 머신 러닝 더 빠르고 정확하게

scikit-learnn과 같은 머신러닝 라이브러리에는 복잡한 알고리즘이 이미 구현되어 있어 이론적인 걸 잘 몰라도 매우 편리하게 사용할 수 있다.
하지만 이러한 라이브러리들도 아무렇게나 사용하면 성능이 떨어질 수 있기 때문에 이제부터는 머신 러닝 알고리즘의 속도와 정확도를 높이기 위한 이론 몇 가지를 배울 예정이다. 이 내용들은 그동안 배운 알고리즘들 뿐만 아니라 다른 수많은 알고리즘들에도 적용할 수 있다.

02. Feature Scaling : Normalization

• 데이터 전처리
  주어진 데이터를 그대로 사용하지 않고 가공하여 머신 러닝 모델을 학습시키기 더 좋은 형식으로 만들어 주는 것
  
  
• Feature Scaling
  전처리 과정 중 하나로, 입력 변수(feature)의 크기를 조정(scale)해 일정 범위 내에 떨어지도록 바꿔주는 것이다.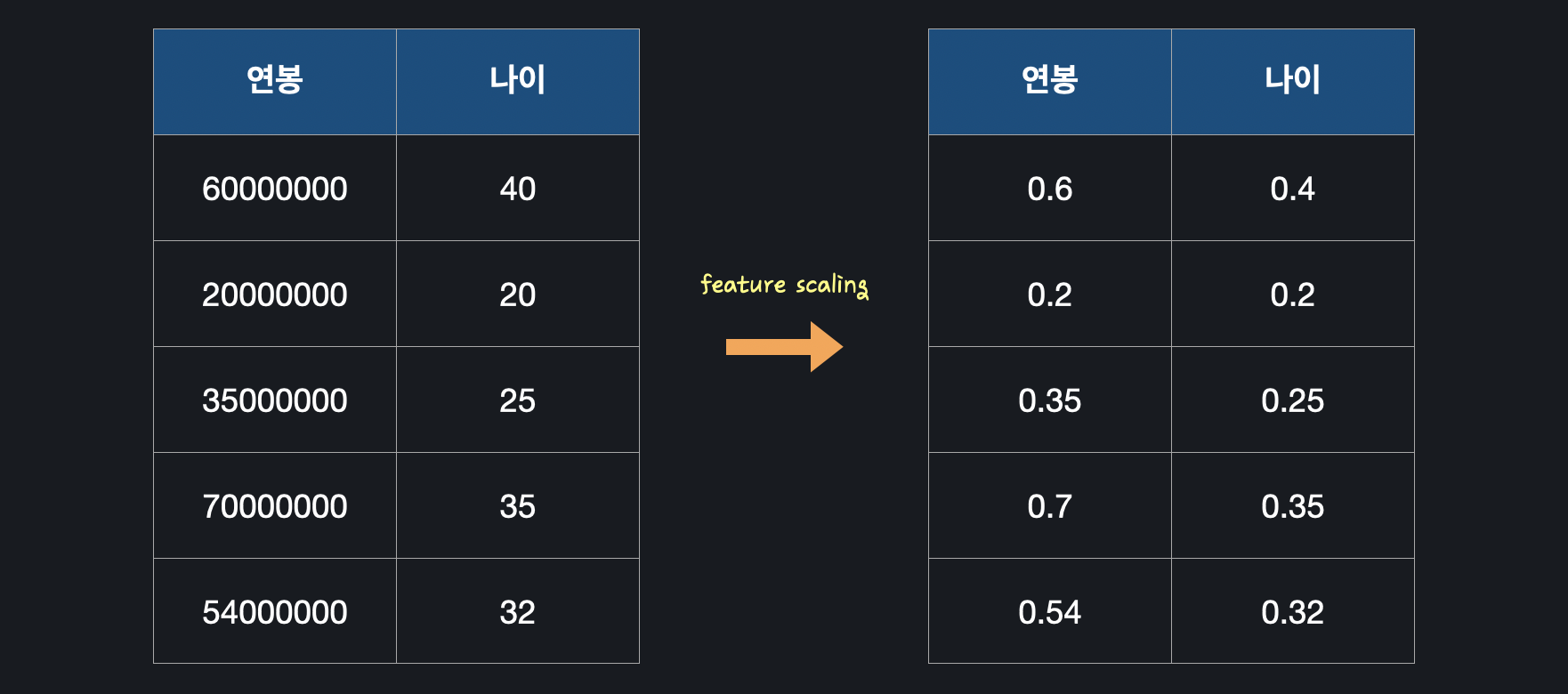예를 들어 연봉과 나이라는 2개의 입력 변수가 있다고 가정하면, 연봉과 나이의 규모 단위가 너무 차이가 나 머신 러닝에 방해가 될 수 있다. 따라서 feature scaling을 해서 입력 변수들의 크기가 모두 일정 범위 내에 들어오도록 조정해준다.
  
  1. Min-Max Normalization
  feature scaling을 하는 여러 방법 중 하나로, 가장 직관적인 방법이다. normalization은 '숫자의 크기를 0과 1 사이로 만든다' 라는 뜻이다.
  Min-Max Normalization는 데이터의 최솟값(minimum), 최댓값(maximum)을 이용해 데이터의 크기를 0 ~ 1 사이로 바꿔준다. min-max normalization 공식은 아래와 같다.
  
  $x_{new} = \frac{x_{old} - x_{min}}{x_{max} - x_{min}}$
  
  
  $x_{new}$ : normalization을 한 데이터
  $x_{old}$ : normalization 하기 전 데이터
  $x_{max}$ : 데이터의 최댓값
  $x_{min}$ : 데이터의 최솟값
  
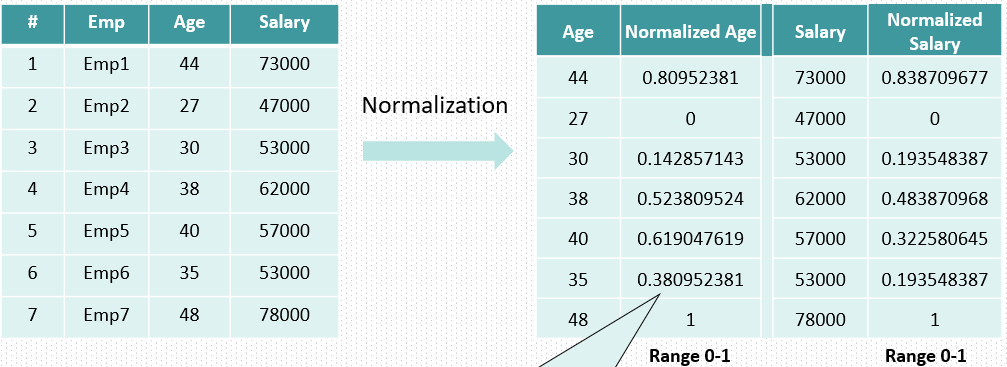  보다시피 normalization 해주면 모든 데이터 값을 항상 0과 1 사이의 작은 숫자로 바뀌는 것을 볼 수 있다.
  
  2. Standardization(표준화)
  표준화를 하기 위해선 평균과 표준 편차를 알아야 한다.
  n개의 데이터 $x_1$, $x_2$, ... , $x_n$ 가 있을 때,
  데이터의 평균은 $\bar{x} = \frac{x_1 + x_2 + ... + x_n}{n}$,
  데이터의 표준 편차는 $\sigma = \sqrt{\frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + ... + (x_n - \bar{x})^2}{n}}$이다. 표준화 공식은 아래와 같다.
  $x_{new} = \frac{x_{old} - \bar{x}}{\sigma}$
  
  $x_{new}$ : 표준화한 데이터
  $x_{old}$ : 표준화하기 전 데이터
  $\bar{x}$ : 데이터의 평균
  $\sigma$ : 데이터의 표준 편차
  
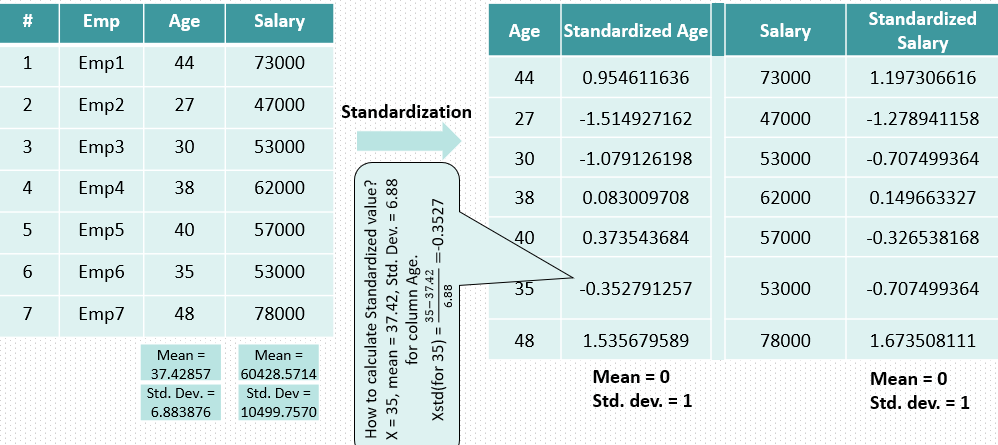  이처럼 표준화를 사용해서 데이터들을 일정한 크기의 숫자들로 조정해줄 수 있다. 표준화를 하면 항상 새로운 데이터의 평균은 0, 표준 편차는 1이 된다. 이렇게 표준화를 해준 데이터를 'z-score'라고도 하는데, z-score는 데이터가 평균 값에서 몇 표준 편차만큼 떨어져 있는지를 뜻한다.
  
  
• Feature Scaling과 경사 하강법

  Review)

  • 선형 회귀
    데이터에 가장 잘 맞는 선 또는 가설 함수 $h_{\theta}(x) = \theta_0 + \theta_1x$을 찾는 것
    데이터에 가장 잘 맞는다 = 데이터에 대한 평균 제곱 오차를 최소화한다
    
    평균 제곱 오차 $MSE= \frac{1}{m}\sum_{i=1}^m(h_{\theta}(x^{(i)} - y^{(i)})^2$,
    손실 함수 $J(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_{\theta}(x^{(i)} - y^{(i)})^2$는 가설 함수를 평가하기 위한 함수로, 평균 제곱 오차로 정의한다.
    
    손실 함수 아웃풋이 크다 -> 가설 함수가 안좋다
    손실 함수 아웃풋이 작다 -> 가설 함수가 좋다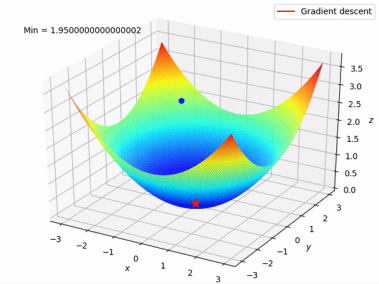손실 함수 그래프에서 $x$축은 $\theta_0$, $y$축은 $\theta_1$, $z$축은 손실을 나타낸다.
    경사 하강법은 어떤 지점에서 경사가 가장 가파른 방향으로 조금씩 이동하면서 그래프 상에서 손실이 가장 적은 지점에 해당하는 최적의 $\theta$값들을 구하는 방법이다.

손실 함수 3차원 그래프를 2차원 상으로 표현하면 다음과 같다.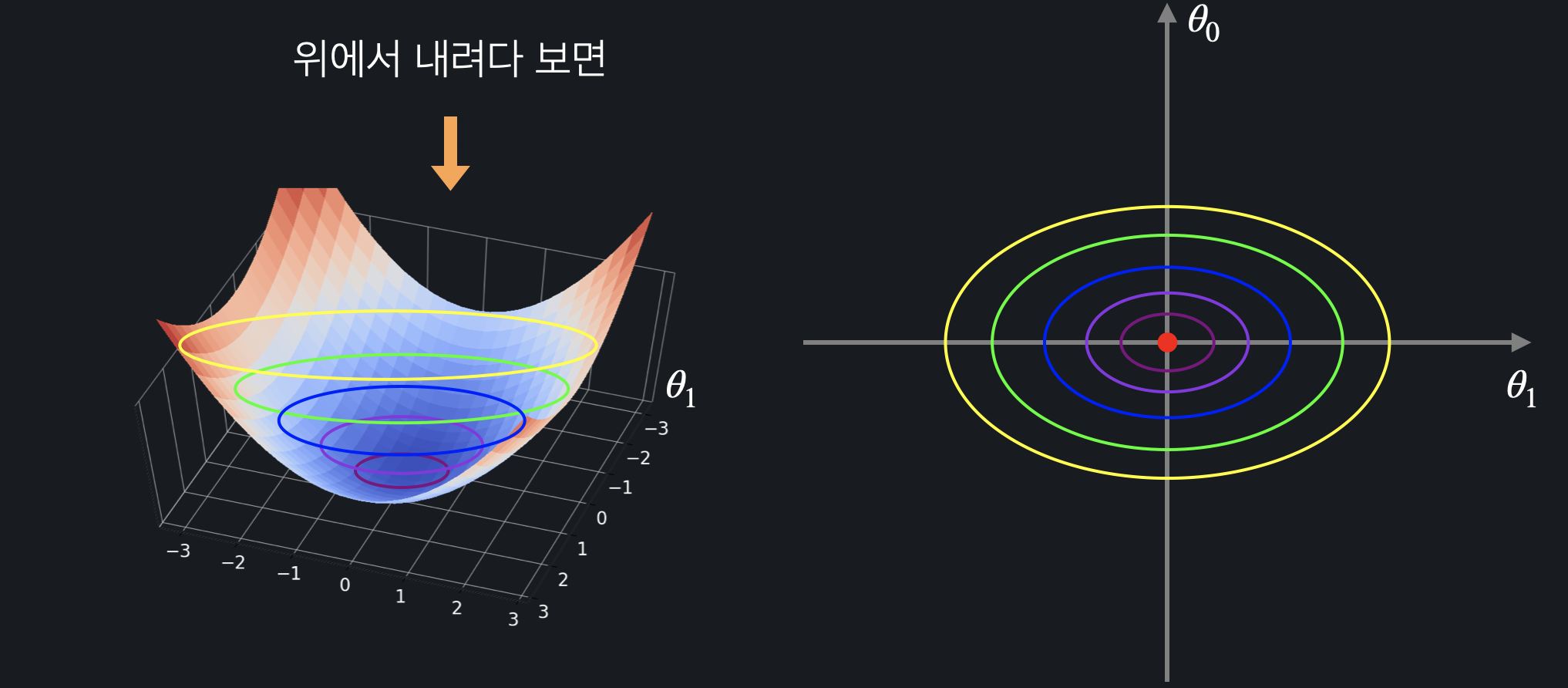등고선 색상이 노랑 > 초록 > 파랑 > 남색 > 보라 순으로 더 손실이 작은 부분을 나타내고 중간에 빨간 점이 손실이 가장 작은 부분(최소점)이다.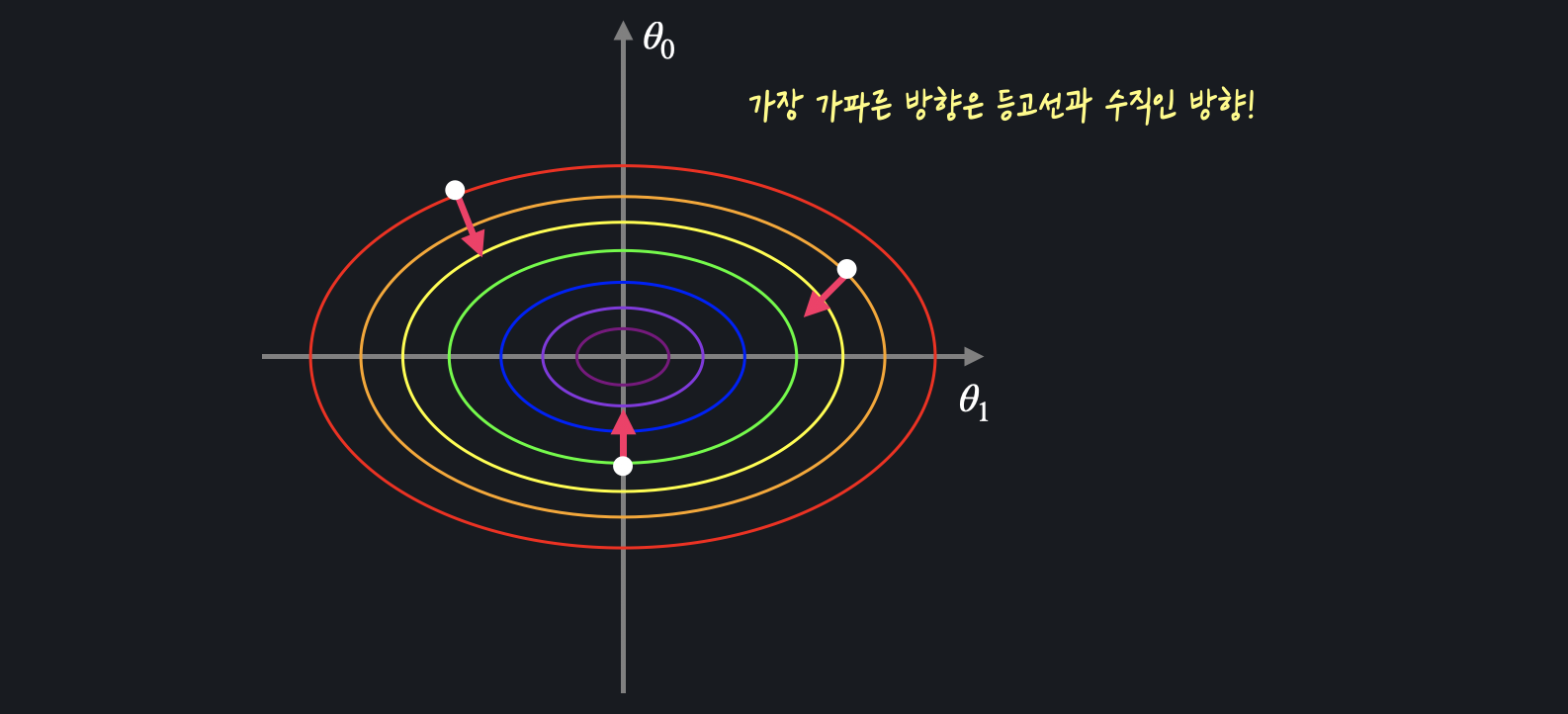2차원 상으로 그래프를 그리면,
특정 지점에서 경사가 가장 가파른 방향 = 등고선과 수직이 되는 방향이라는 것을 알 수 있다.

연봉을 가지고 나이를 예측하는 선형 회귀 $h_{\theta}(x) = \theta_0 + \theta_1x$를 한다고 가정하면,

• normalization 하지 않았을 때
  $\theta_1$은 천만 단위 숫자인 연봉과 곱해지기 때문에 $\theta_1$의 값이 조금만 바뀌어도 가설 함수의 아웃풋이 엄청나게 변하게 된다. 하지만 $\theta_0$은 항상 1과 곱해지기 때문에 값이 어느정도 바뀌어도 아웃풋에 큰 변화를 주지 않는다.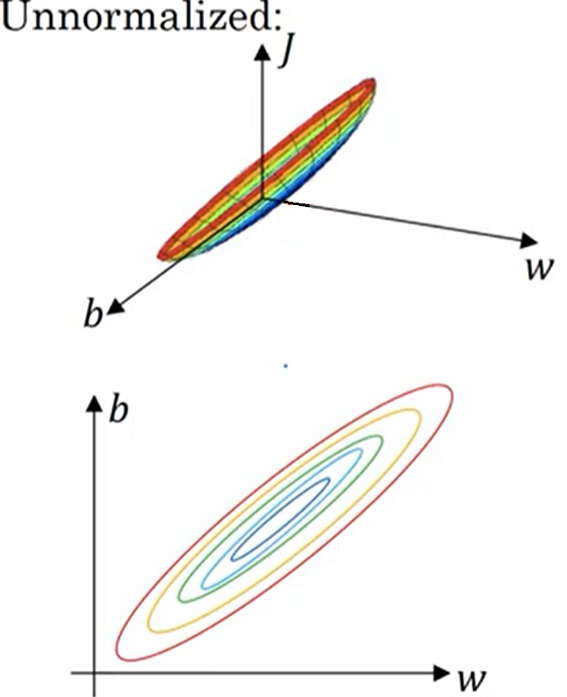가설 함수 아웃풋에 큰 영향을 준다는 것은 손실 함수에도 큰 영향을 준다는 것과 같고 $\theta_1$방향(y축) 방향으로 조금만 움직여도 손실이 급격히 증가하거나 감소하게 된다.
• normalization 했을 때
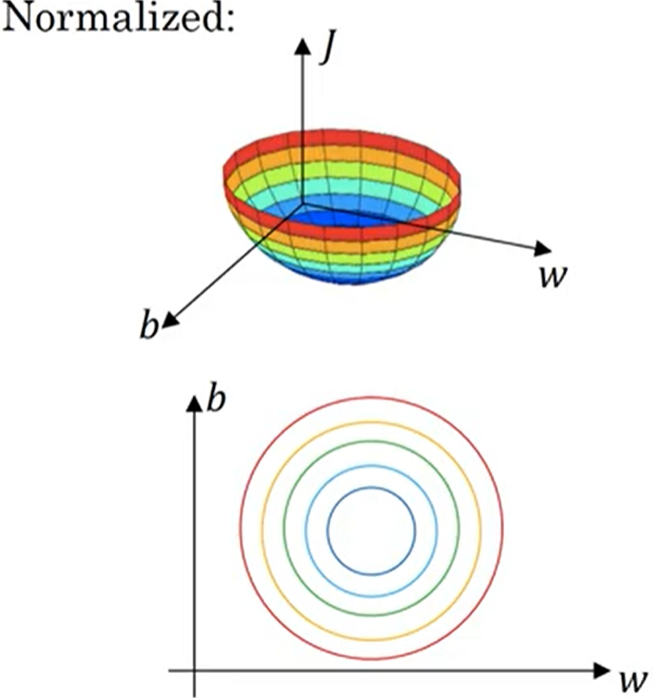  만약 normalization으로 feature scaling을 한다면, 연봉이 0과 1 사이의 숫자들로 바뀌면서 $\theta_0$과 $\theta_1$에 비슷한 숫자들이 곱해지기 때문에 손실 함수에 비슷한 영향을 주게 된다.
  
  위 두 그래프에서 경사 하강을 해보면
  normalization을 하지 않은 경우, 지그재그 모양으로 그래프를 내려오고
  normalization을 한 경우, 더 직선에 가까운 형태로 내려오게 된다.
  
  normalization을 하면 어떤 지점이든 경사가 가장 가파른 방형이 최소점을 향하는 방향이기 때문에 가장 가파른 경사를 따라서 내려오면 훨씬 더 빨리 최소점을 찾을 수 있다.
  이처럼 feature scaling을 해주면 선형 회귀뿐만 아니라 다항 회귀, 로지스틱 회귀 등 경사 하강법을 사용하는 모든 알고리즘에서 더 빠르게 모델을 학습시킬 수 있다.
  
  
  

03. One-hot Encoding

머신 러닝에 사용되는 데이터는 나이, 몸무게, 키와 같은 수치형(numercial) 데이터와 혈액형, 성별과 같은 범주형(categorical) 데이터가 있다.
많은 머신 러닝 알고리즘은 입력 변수의 값이 수치형 데이터여야 하기 때문에, 범주형 데이터가 있다면 수치형 데이터로 변환해줘야 한다.

• 자연수를 범주형 데이터의 각 카테고리에 지정해주는 방법
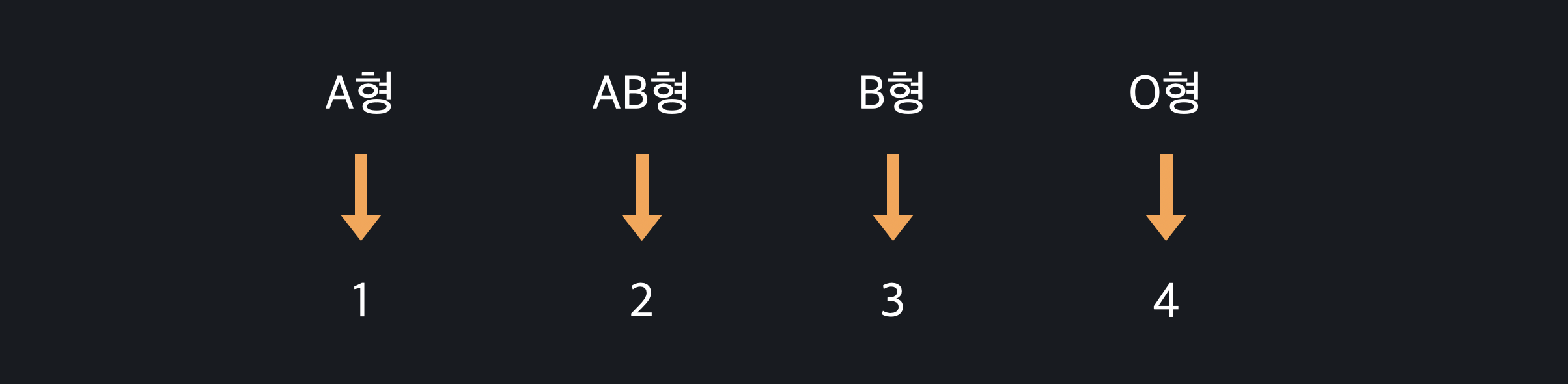  가장 단순한 방법이지만 이렇게 데이터를 바꿔주게 되면 혈액형에 크고 작다는 개념이 생기게 된다. 'A형은 1이니까 가장 작고, O형을 4니까 가장 크고, AB형과 B형을 그 사이다'라는 관계가 생기고 머신 러닝 알고리즘은 이런 엉뚱한 관계도 학습하기 때문에 오히려 예측에 방해가 될 수 있다.
  

• One-hot Encoding
  one-hot Encoding을 하면 범주형 데이터에게 크고 작음의 엉뚱한 관계가 생기는 걸 방지하면서도 수치형 데이터로 바꿔 줄 수 있다.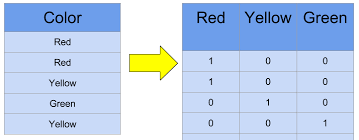
  step 1) 데이터의 각 카테고리를 하나의 새로운 열로 만들어 준다.
  step 2) 주어진 데이터가 어떤 값인지에 따라 새로운 열들의 값을 0 또는 1로 채워준다.
  각 열들은 0과 1, 두 값만 가지기 때문에 범주형 데이터에게 크고 작은 관계가 생기는 것을 막을 수 있다.

+) one-hot encoding의 단점 : 클래스의 라벨이 너무 많은 경우(카테고리가 많은 경우), one-hot encoding으로 변환하면 데이터의 크기가 너무 방대해져 오히려 학습이 힘들어진다는 문제가 발생할 수 있다.