- 코드잇 강의 바로 가기

정규화

01. 편향과 분산

• 편향(Bias)
  
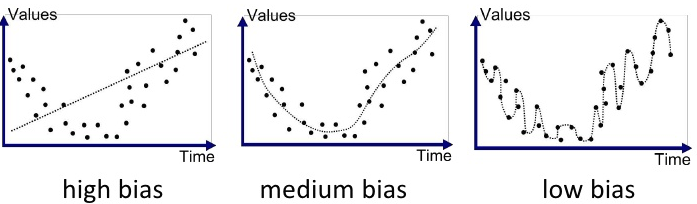
  왼쪽과 같이 선형 회귀로 직선 모델을 나타냈을 때, 아무리 학습해도 곡선 관계를 나타내지 못하는 한계가 있다.
  반면 오른쪽처럼 높은 차항의 회귀를 사용해서 모델을 학습시키면, 이 복잡한 곡선은 training 데이터에 거의 완벽하게 맞춰지게 된다.

  • 모델이 너무 간단해서 데이터의 관계를 잘 학습하지 못하는 경우
    = 모델의 편향이 높다.
  • 모델의 복잡도를 높여서 training 데이터의 관계를 잘 학습한 경우
    = 모델의 편향이 낮다.

Q. 편향이 낮은 모델은 항상 편향이 높은 모델보다 좋을까?
A. 꼭 그렇지만은 않다.

• 분산(Variance)
  다양한 테스트 데이터가 주어졌을 때 모델이 얼마나 일관된 성능을 보여주는지 나타내는 값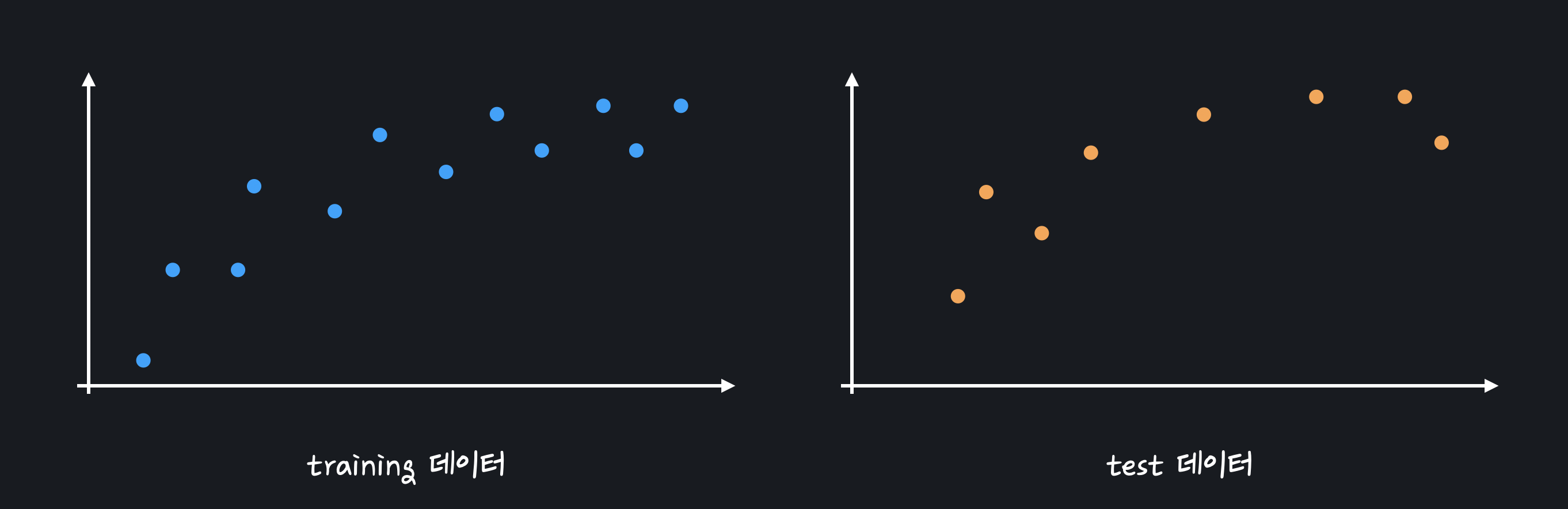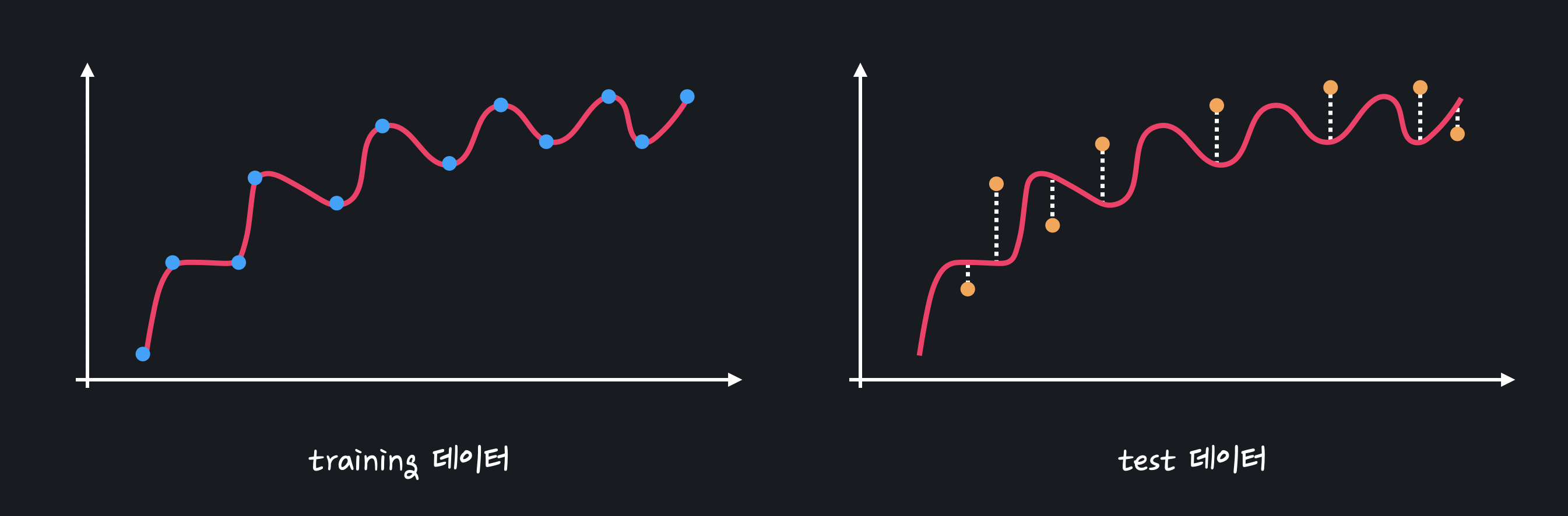직선 모델과 복잡한 곡선 모델을 이용해 처음 보는 test 데이터의 결과를 예측할 때,
  복잡한 모델을 training 데이터에서는 거의 완벽한 성능을 보이지만 test 데이터에 대해서는 성능이 좋지 않은 것을 볼 수 있다.
  모델이 너무 복잡해서 training 데이터를 가지고 학습할 때 데이터 간의 관계를 배우기보단 아예 데이터 자체를 외워버리기 때문에 오히려 처음 보는 데이터에서는 성능이 아주 떨어지는 문제가 발생한다.
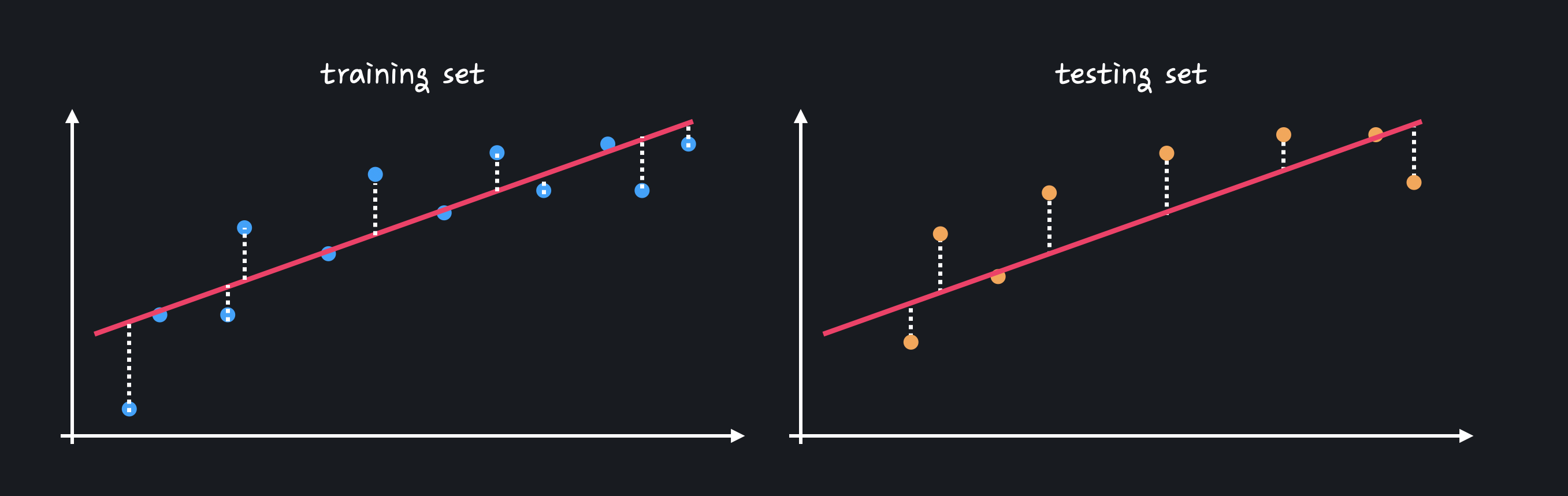  직선 모델은 training 데이터와 test 데이터에서의 성능을 비교했을 때 큰 차이가 없음을 볼 수 있다.

  • 다양한 데이터 셋에 대해 성능 차이가 많이 나는 경우
    = 분산이 높다.
  • 다양한 데이터 셋에 대해 성능이 비슷한 경우
    = 분산이 낮다.

• 편향-분산 트레이드오프(Bias-Variance Tradeoff)
  직선 모델 : 복잡도가 너무 떨어져 데이터 간의 곡선 관계를 학습할 수 없어 편향이 높지만, 모델이 간단하기 때문에 어떤 데이터가 주어지든 일관된 성능을 보여 분산이 낮다.
  = 모델이 training 데이터에 과소적합(underfitting) 되었다.

  복잡한 곡선 모델 : trainig 데이터 자체를 외워버려 training 데이터에 대한 성능은 매우 높아 편향이 낮지만, 새로운 test 데이터에 대한 성능은 많이 떨어져 분산이 높다.
  = 모델이 training 데이터에 과적합(overfitting) 되었다.

편향과 분산은 반비례 관계로, 둘 중 하나를 줄이기 위해서는 다른 하나를 포기해야 한다. 이러한 관계를 편향-분산 트레이드오프라고 하고, 이 문제는 머신 러닝 프로그램의 성능과 밀접한 관계가 있기 때문에 편향과 분산(과소적합과 과적합)의 적당한 밸런스를 찾아내는 것이 중요하다.

02. 정규화(Regularization)

정규화는 손실 함수에 '정규화 항'을 더해 $\theta$값들이 커지는 것을 방지해 학습 과정에서 모델이 과적합 되는 것을 예방해준다.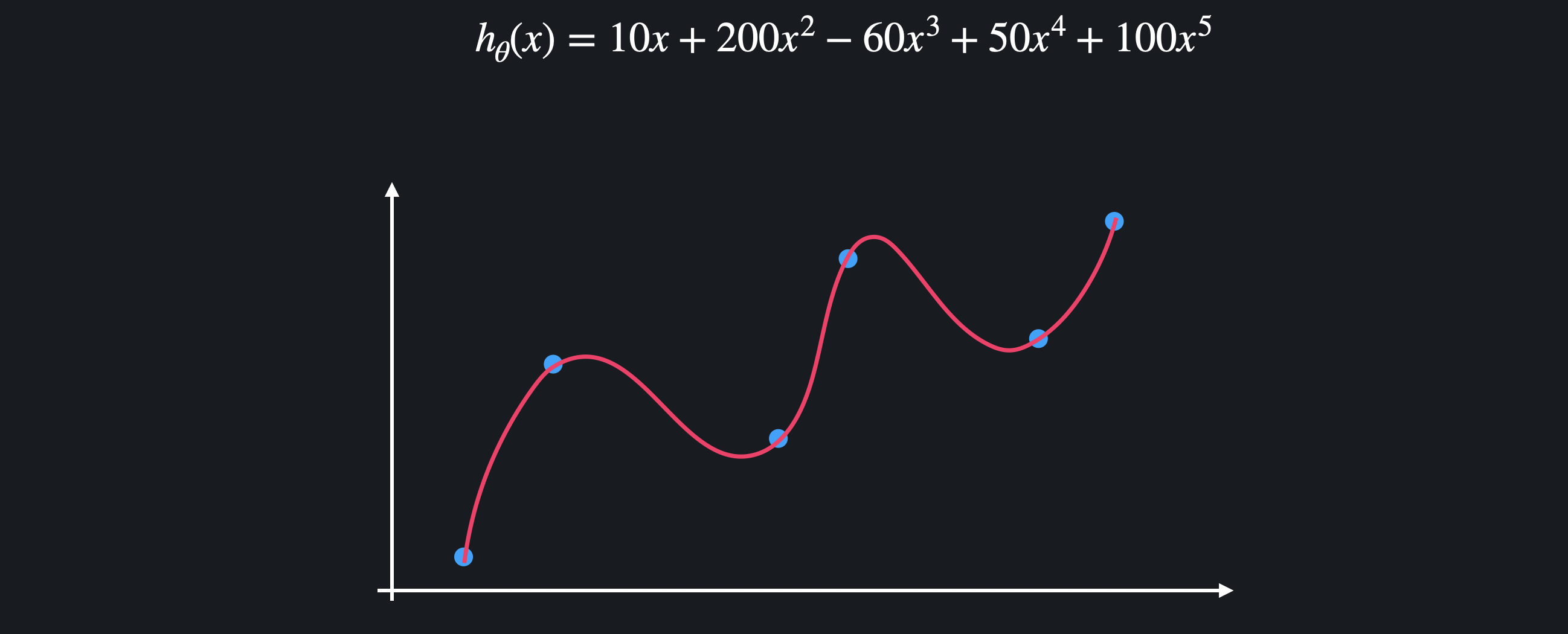모델이 과적합 돼서 복잡한 다항 함수가 나왔다고 가정한다.
보통 과적합된 함수는 많은 굴곡을 이용해서 함수가 training 데이터를 최대한 많이 통과하도록 하기 때문에 위아래로 엄청 왔다갔다 한다는 특징이 있다.
함수가 이렇게 급격하게 변한다는 것은 가설 함수의 $\theta$값들이 굉장히 크다는 뜻이다.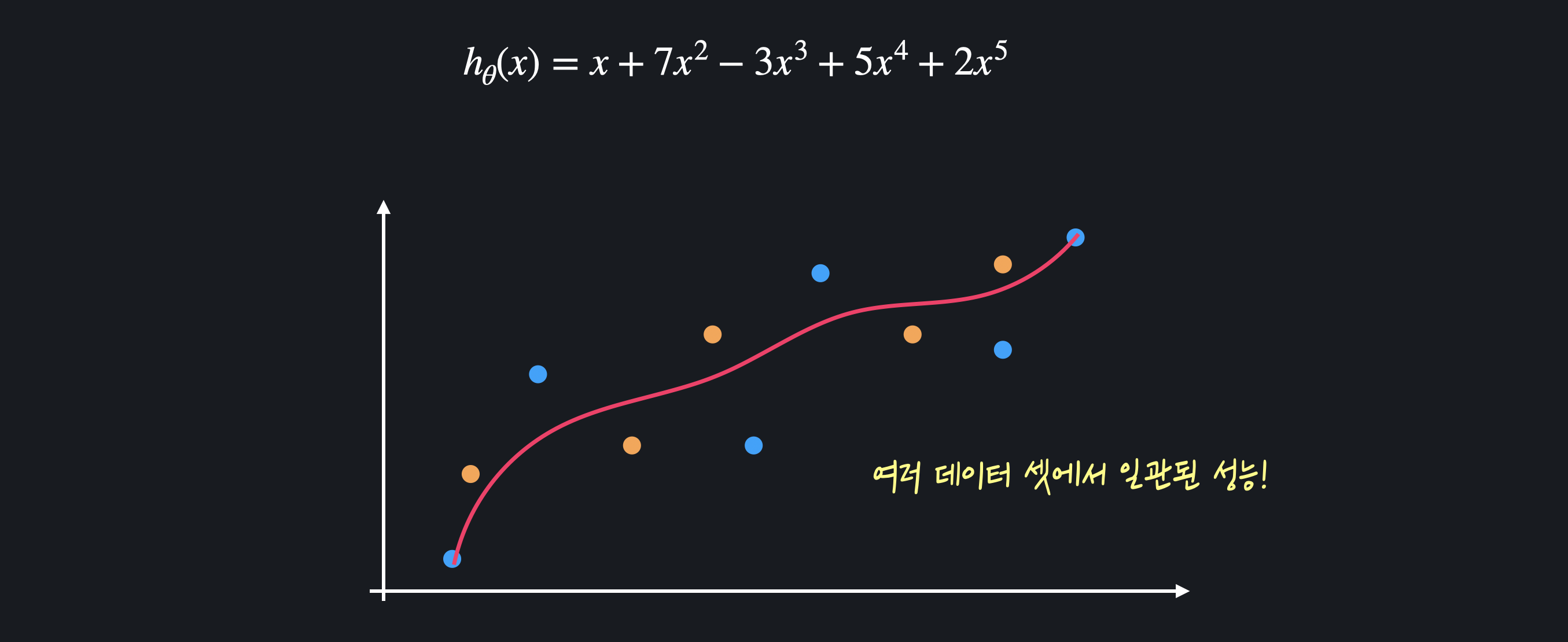정규화는 모델을 학습시킬 때 $\theta$값들이 과도하게 커지는 것을 막아 가설 함수를 좀 더 완만하게 만들 수 있다. 이런 완만한 가설 함수는 여러 데이터 셋에 대해 더 일관된 성능을 보이기 때문에 과적합을 막을 수 있다.

Review)
예를 들어 다항 회귀에서는 위처럼 데이터에 가장 잘 맞는 선 $h_{\theta}(x) = \theta_0 + \theta_1x + ... + \theta_nx^n$을 찾는 것이 목적이다.
평균 제곱 오차(MSE)를 이용한 손실 함수
$J(\theta) = \frac{1}{2m}\sum_{i=1}^m{h_\theta(x^{(i)}) - y^{(i)})^2}$의 아웃풋이 작을수록, 즉 "training 데이터에 대한 평균 제곱 오차가 작을수록" 좋은 가설 함수로 평가했다.

하지만 위 모델은 $\theta$값들이 너무 커서 training 데이터에 과적합 되었다는 문제가 발생했다. 이를 해결하기 위해서는 좋은 가설 함수의 기준을 바꿔줌으로써 정규화를 할 수 있다.

• 좋은 가설 함수란,

1. training 데이터에 대한 MSE가 작아야 한다.
2. $\theta$값들이 작아야 한다.

이를 수학적으로 표현하면 아래와 같다.

• L1 정규화

  $J(\theta) = \frac{1}{2m}\sum_{i=1}^m{h_\theta(x^{(i)}) - y^{(i)})^2} + \vert\theta_1\vert + \vert\theta_2\vert + ... + \vert\theta_n\vert\\ = \frac{1}{2m}\sum_{i=1}^m{h_\theta(x^{(i)}) - y^{(i)})^2} + \sum_{i=1}^n{\vert\theta_i\vert}$

  이 때 $\sum_{i=1}^n{\vert\theta_i\vert}$을 정규화 항이라 하고, $\theta_0$은 과적합과 상관없기 때문에 $\theta_0$의 절댓값은 더해주지 않는다.
  예를 들어, 다음 두 가설 함수가 있다고 가정한다.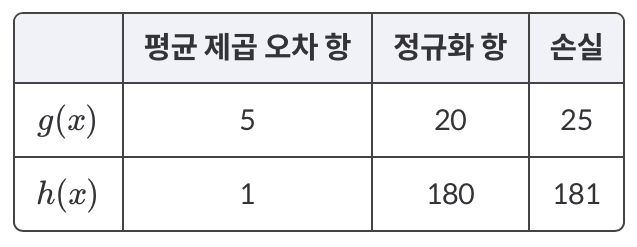

  $g(x) = 5 + 10x - 2x^2 + 5x^4 + 3x^5\\ h(x) = 20 + 40x - 70x^2 + 50x^4 + 20x^5$

  이러한 손실 함수 표를 구할 수 있고 $g(x)$가 총 손실이 더 작기 때문에 더 좋은 가설 함수라고 평가한다.
  
  
  사실 정규화 항에는 아래와 같이 $\lambda$라는 상수를 곱해준다.

  $J(\theta) = \frac{1}{2m}\sum_{i=1}^m{h_\theta(x^{(i)}) - y^{(i)})^2} + \lambda\sum_{i=1}^n{\vert\theta_i\vert}$

  $\lambda$는 $\theta$값들이 커지는 것에 대해 얼마나 많은 패널티를 부여할지 정해주는 값으로, 데이터에 대한 오차와 $\theta$값 중 어떤 것을 줄이는 게 더 중요한지 결정한다.

  $\lambda$가 클수록 $\theta$값들이 조금만 커져도 총 손실이 굉장히 커지기 때문에 $\theta$값을 줄이는 게 중요하고, $\lambda$가 작을수록 $\theta$값들이 커져도 손실이 별로 커지지 않기 때문에 MSE를 줄이는 게 중요하다.

  이처럼 L1 정규화를 사용하는 회귀 모델을 Lasso (회귀) 모델이라고 한다.

• L2 정규화

  $J(\theta) = \frac{1}{2m}\sum_{i=1}^m{h_\theta(x^{(i)}) - y^{(i)})^2} + \lambda\sum_{i=1}^n{\theta_i^2}$

  L2 정규화를 사용하는 회귀 모델을 Ridge (회귀) 모델이라고 한다.
  
  

• L1 정규화 VS. L2 정규화
  

• L1 정규화
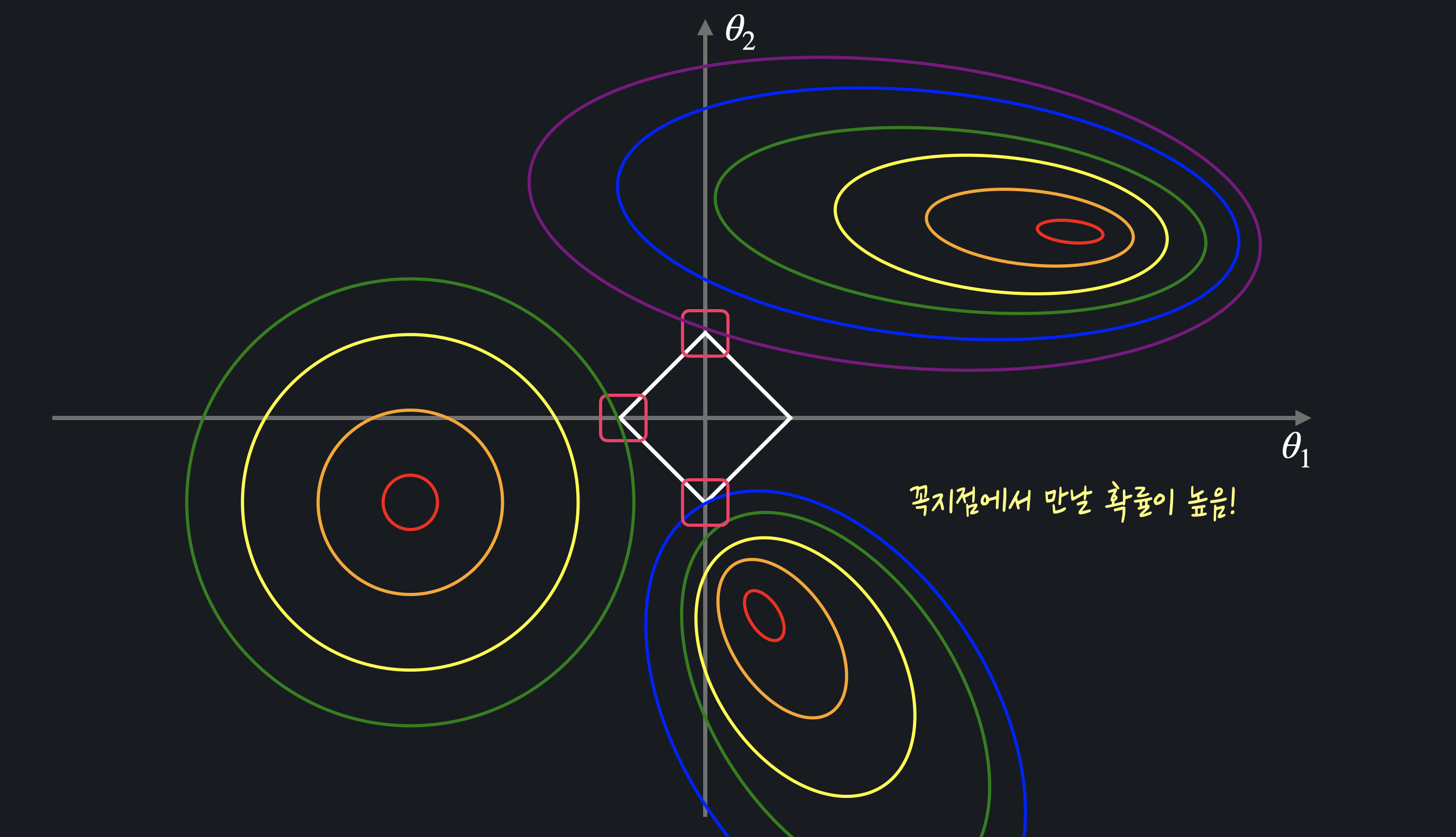
  그래프 상의 마름모 : 경사 하강법을 통해 찾은 최적의 $\theta$를 통해 계산한 정규화 항 $t$의 등고선($\vert\theta_1\vert + \vert\theta_2\vert = t$)

  $J(\theta) = \frac{1}{2m}\sum_{i=1}^m{h_\theta(x^{(i)}) - y^{(i)})^2} + t$에서 $t$는 고정돼 있기 때문에 손실을 최소화하기 위해서는 MSE만 최소화하면 된다.
  MSE를 최소화하는 점을 찾기 위해서는 MSE의 등고선이 마름모에 닿을 때까지 조금씩 더 큰 등고선을 그려주면 되는데, 그렇게 구한 최소점들은 마름모의 각 꼭짓점일 확률이 높다는 것을 볼 수 있다. 이때 꼭짓점의 좌표값은 $\theta_1$, $\theta_2$ 중 하나가 항상 0이기 때문에 L1 손실 함수를 최소화하는 $\theta_1$, $\theta_2$값은 0일 확률이 높다.

  L1정규화는 여러 $\theta$값들을 0으로 만들어 준다. 따라서 어떤 모델에 쓰이는 속성 또는 변수의 개수를 줄이고 싶을 때 사용한다.
  +) 여러 입력 변수 중 한쪽 값(정의역이 지나치게 큰 경우, 관계 학습에 불필요한 데이터인 경우 등)의 영향력을 줄여주고 싶을 때 사용한다.
  

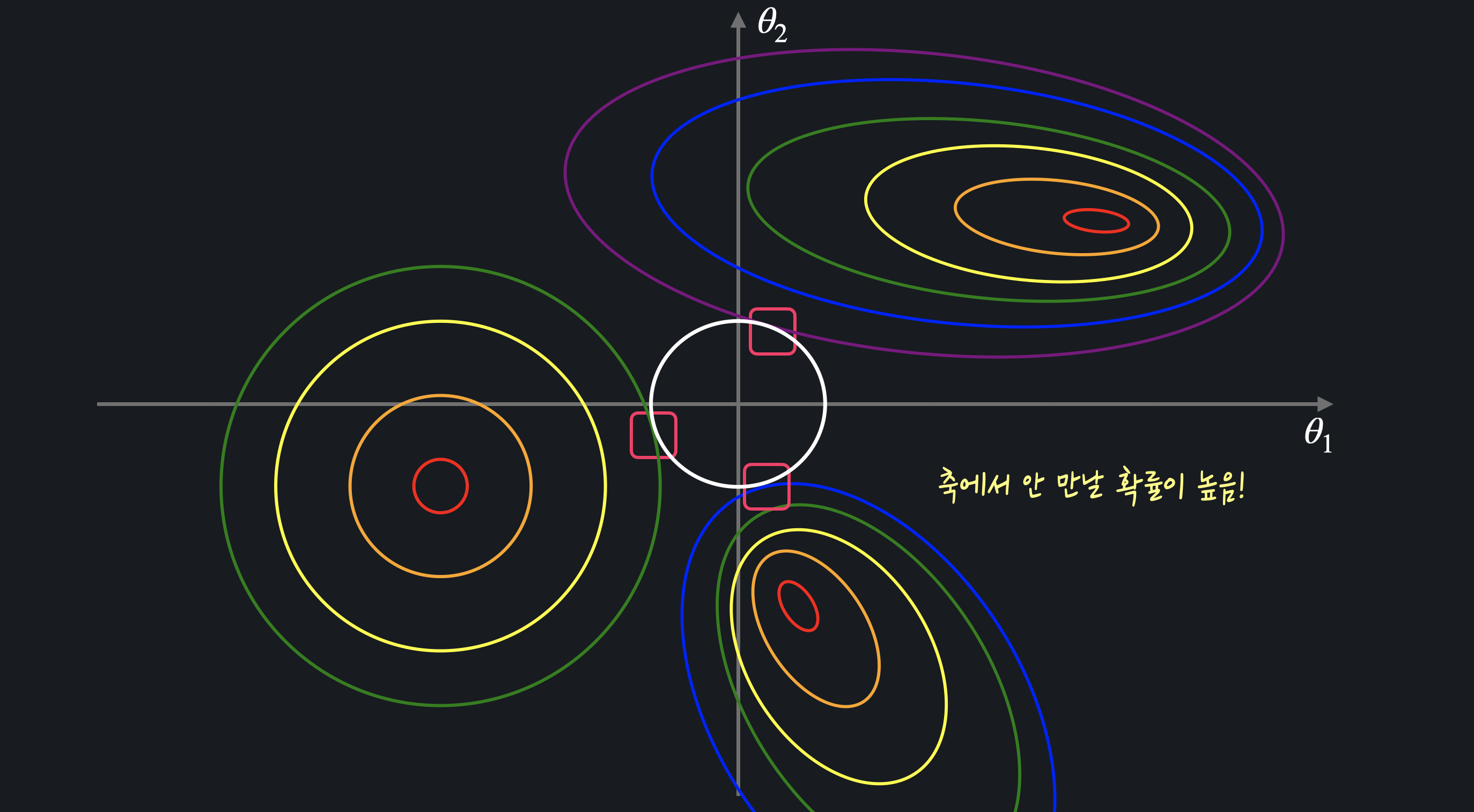
• L2 정규화
  그래프 상의 원 : 경사 하강법을 통해 찾은 최적의 $\theta$를 통해 계산한 정규화 항 $t$의 등고선($\theta_1^2 + \theta_2^2 = t$)

  마름모와는 다르게 원 모양 등고선은 MSE의 등고선과 닿는 지점이 축 위가 아닐 확률이 높다. 따라서 L2 손실 함수를 최소화하는 $\theta_1$, $\theta_2$값은 둘 다 0이 아닐 확률이 높다.

  L2 정규화는 전체적으로 $\theta$값들을 0이 아니라 조금씩 줄여 준다. 따라서 속성의 개수를 딱히 줄일 필요가 없다고 생각될 때 사용한다.
  +) 입력 변수들의 영향력이 모두 비슷할 때 전반적으로 데이터들의 크기를 줄여주는 역할을 한다.