Module 3. 『지도학습(분류/회귀)』 3. Gradient Discent

📍 강의 자료 출처 : LG Aimers

Gradient Discent Algorithm & 최적화 방식

Overview

Gradient Discent의 목적 : objective 함수 최소화하는 $θ$ 찾기

• $α$가 너무 작으면 수렴하는 형태가 안정적이지만 속도가 매우 느리다.
• $α$가 너무 크면 error surface 상에서 최소인 지점을 찾기 어렵고 발산하는 형태로 학습이 진행된다.
  (= loss가 오히려 늘어나는 방향으로, 학습이 되지 않는다)

---

Gradient Discent

Batch gradient descent

: 가장 기본적인 형태로, overview에서 설명하는 경사하강법을 의미한다.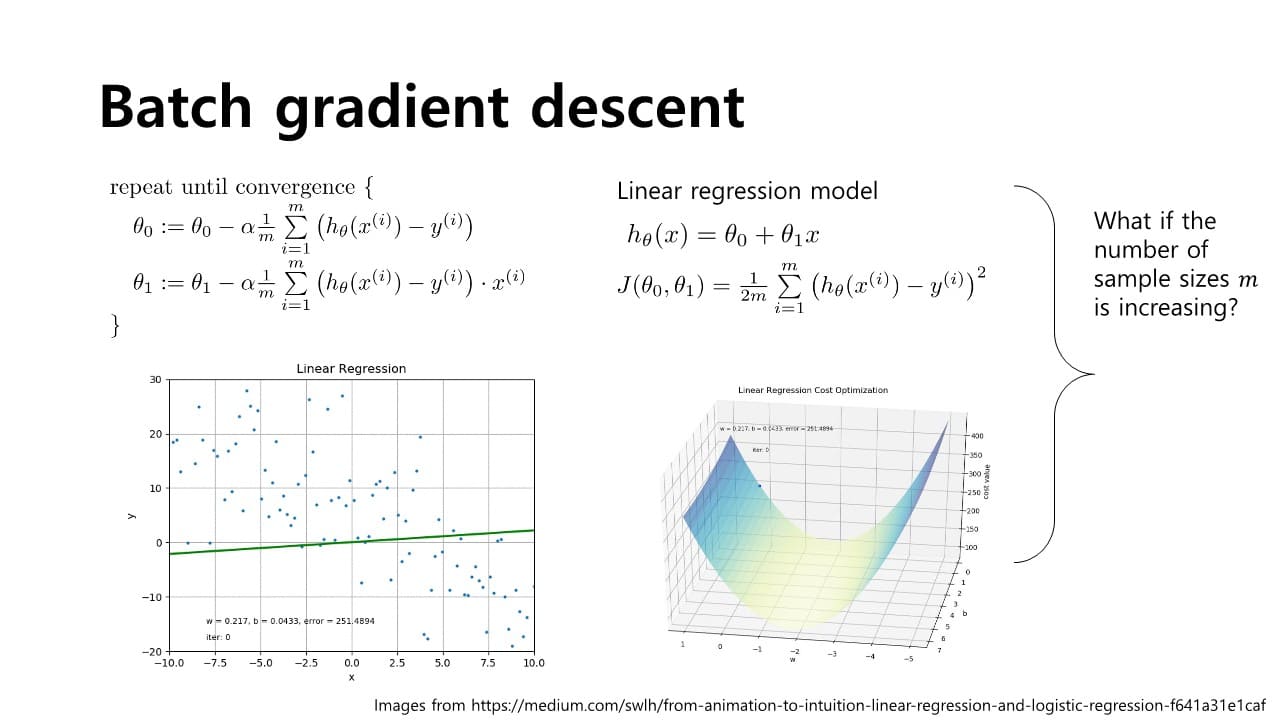linear regression model에서 목적함수 $J$의 partial derivative term을 넣어서 각각 $θ_0$와 $θ_1$을 바꾸는 것을 볼 수 있다.

• 단점
  $θ_0$와 $θ_1$를 업데이트하는 과정에서 전체 샘플 m개를 모두 고려해야 한다.
  → 모든 샘플애 대해 축적해야 $θ$를 한 번 업데이트할 수 있다.
  
  

Stochastic gradient descent(SGD)

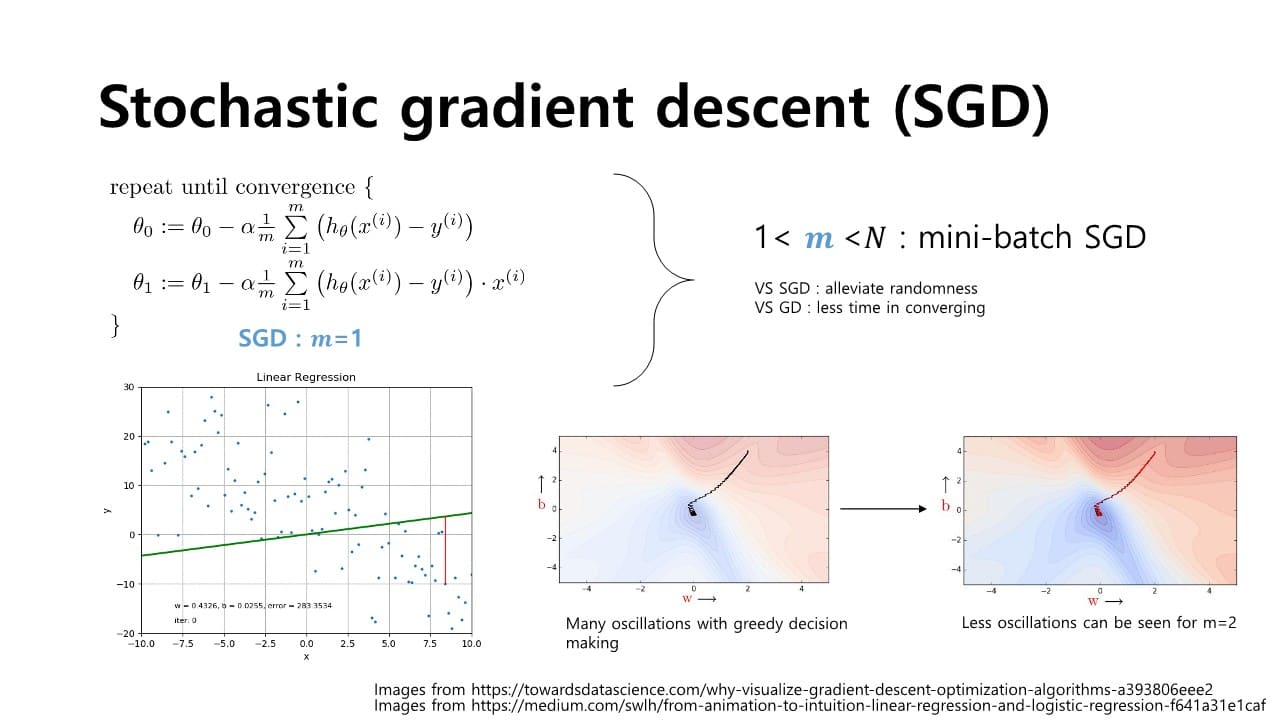
• 장점
  Batch gradient descent에 비해 빠르게 iteration 가능하다.
• 단점
  • 각 샘플 하나하나마다의 계산을 통해 parameter를 연산하기 때문에 noise에 영향을 받기 쉬움
  • saddle point와 같이 기울기가 0이 되어 local minimum에 빠지는 문제가 발생하기 쉬움
    
    

Momentum

local minimum에 빠지게 되는 문제를 해결하기 위한 방법 중 하나이다.

Momentum $v$: 과거에 Gradient가 업데이트 되어오던 방향 및 속도를 어느 정도 반영해서
현재 포인트에서 Gradient가 0이 되더라도 계속해서 학습을 진행할 수 있는 동력을 제공하게 되는 것

= exponentially weighted moving average
항상 $ρ$ < 1이기 때문에 $ρ$를 연속적으로 곱하게 되면 값이 점점 작아진다.
→ 먼 과거의 값은 더욱 작아지게 되고 비교적 가까운 거리의 과거 기울기는 적게 작아진
다.

low passing filtering 연산이기 때문에 현재 위치에서의 saddle point나 작은 noise gradient 값의 변화에 보다 안정적으로 수렴할 수 있게 바뀌게 된다.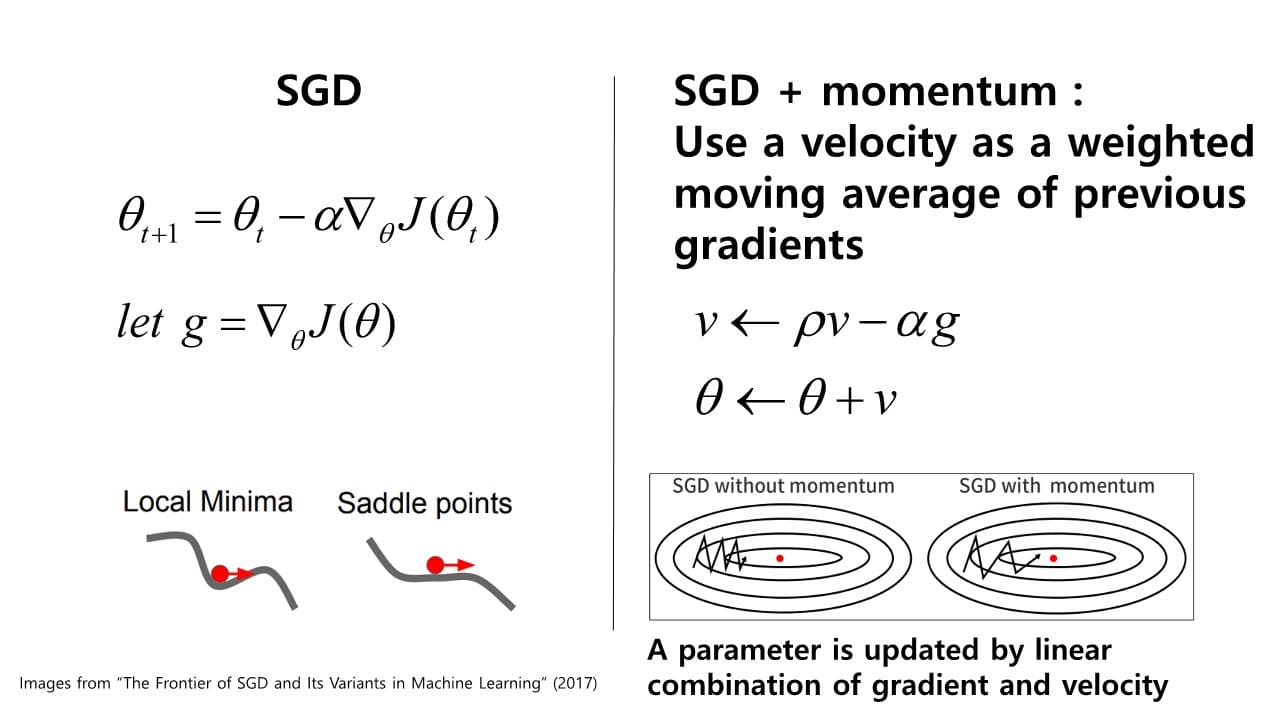⇒ SGD에 monentum을 더해 과거의 값을 반영한 gradient값이 업데이트되도록 만들어 local minimum이나 saddle point처럼 기울기가 0인 지점에 도달하더라도, 과거에 이어오던 momentum 값을 반영해서 계속해서 학습이 진행될 수 있도록 한다.

Nestrov momentum

: 기존의 방식과 달리, gradient를 먼저 평가하고 업데이트하는 방식
= lookahead gradient step 이용
미리 momentum step만큼 이동한 지점에서 lookahead gradient step을 더해 actual step을 계산한다.

AdaGrad

: 각 방향으로의 learning rate를 적응적으로 조절하여 학습효율을 높이는 방식

• 어느 한 방향으로 gradient값이 크다
  = 이미 그 방향으로 학습이 많이 진행되었다
  = gradient 방향으로의 누적합($r$)이 크다
  = $Δθ$ 값이 작아져 그만큼의 수렴 속도를 줄인다
  → 축적된 gradient 값을 통해 learning rate를 조절한다.

• 단점
  gradient값이 계속해서 누적됨에 따라 learning rate값이 굉장히 작아지게 된다.
  = 학습이 일어나지 않게 된다.
  
  

RMSProp algorithm

AdaGrad의 문제점 수정: gradient 방향으로의 누적합($r$)을 업데이트할 때 gradient의 제곱을 그대로 곱하는 것이 아니라
기존에 있던 $r$에 $ρ$값을 곱하고 (1-$ρ$)를 gradient 제곱에 곱해, $r$에 과거의 $r$만큼의 $ρ$ factor를 곱해서 어느 정도 조절하는 방식
→ 어느 정도 완충된 형태로 학습 속도가 줄어든다.

Adam(Adaptive moment estimation)

: RMSProp + Momentum 방식

• 진행 과정
  1. 첫번째 momentum $s$ 계산
  2. RMSProp와 같은 방식으로 두번째 momentum $r$ 계산
  3. 통계적으로 보다 안정된 학습을 위해 bias correction
  4. parameter $θ$ 업데이트

---

Learning rate scheduling

: 학습 과정마다 step size $α$을 적응적으로 줄여나가는 방식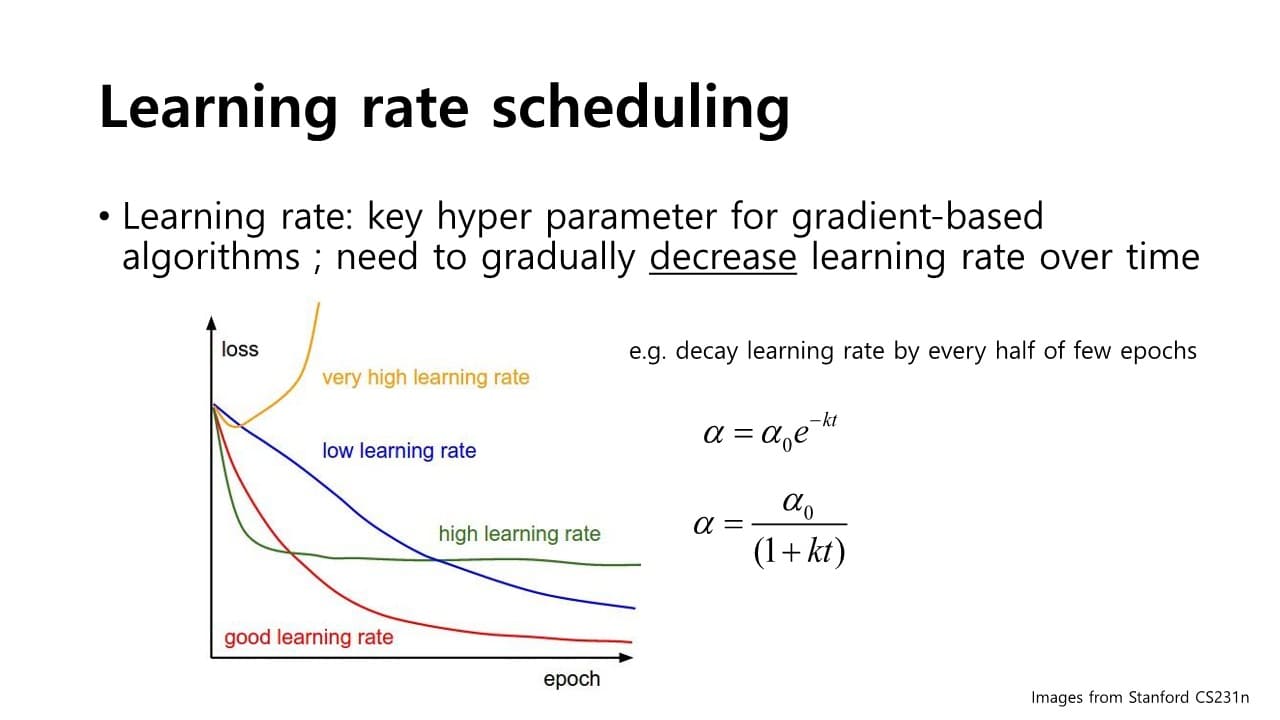

---

Overfitting을 해결하는 최적화 Tip

Model 과적합 문제
: Model이 지나치게 복잡하여(=학습 parameter의 숫자가 많아서)
제한된 학습 샘플에 너무 과하게 학습이 되는 것

Regularization

: 복잡한 모델을 사용하더라도 학습 과정에서 복잡도에 대한 패널티를 부여하여 과적합되지 않도록 하는 방식모델 입장에서는 가능한 한 $θ$를 사용하지 않으면 loss를 최소화하기 위해 노력할 것

$θ$를 쓰지 않는다 ⇔ $θ = 0$
→ parameter의 개수를 줄임으로써 모델의 복잡도를 줄일 수 있다.