Module 3. 『지도학습(분류/회귀)』 4. Linear Classification

YSL·2023년 1월 15일

LG Aimers

목록 보기

13/30

📍 강의 자료 출처 : LG Aimers

classification은 모델의 출력이 discrete한 값을 가지게 된다.
→ decision boundary의 정확한 추정을 통해 주어진 입력에 대해 출력의 분류를 수행하는 문제

Bianary classification

$d$ 차원의 입력 feature vector가 있다고 할 때,
binary classification의 경우 출력값은 yes / no 2가지
→ 목적 : target function $f$ 를 approximation하는 hypothesis $h$ 를 학습하는 것

linear regression과 마찬가지로,
linear model을 사용하는데 $w$ 는 모델의 파라미터, $x$ 는 입력 feature를 의미한다.

그림 상의 점선이 2차원 공간을 분류하는 Hyper plane $h(x) = 0$ 이다.
$h(x) > 0$ 이면 positive sample 이고
$h(x) < 0$ 이면 negative sample이라 할 수 있다.

장점
- 단순하다 = 쉽게 구현할 수 있고 테스트할 수 있다
- 해석 가능하다
- 다양한 환경에서 일반적으로 안정적인 성능을 제공할 수 있다

Multiclass classification

: 입력 신호 공간에서 hyper plane이 다수 존재하여 classification을 수행한다.

One- VS -All

: Binary classification 문제를 Multiclass classification 문제로 확장하는 경우
Binary classification을 여러 개 사용하여 Multiclass classification을 해결할 수 있다.예) 3개의 hyper plane을 그어서 Multiclass classification을 Binary classification으로 푸는 방식

one-hot encoding된 label값과 sigmoid model이 출력하는 확률 값을 서로간에 비교하여 loss function을 통해 error를 계산함으로써 학습 가능하다.

classification의 단계

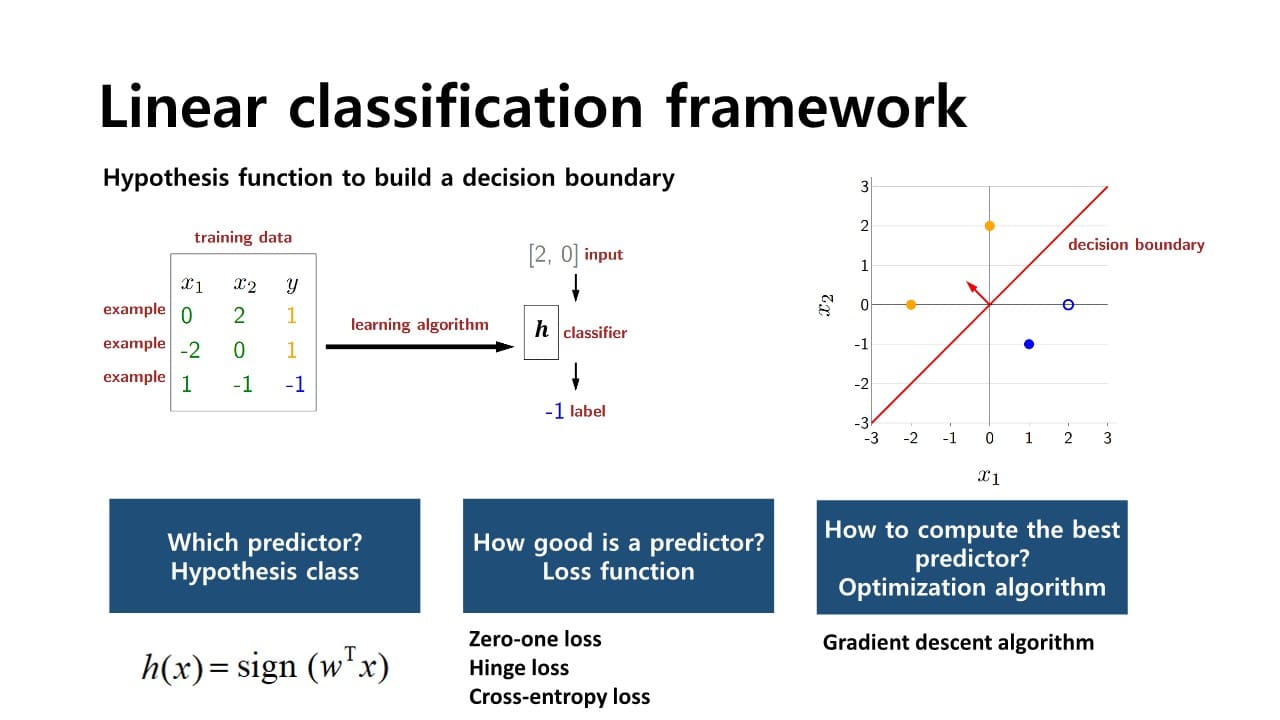
1. 어떤 predictor를 이용할 것인가?

입력 변수와 parameter의 곱으로 score를 계산한다.
$w_0$ : bias (= offset)으로, 입력변수와 parameter은 $(d+1)$ 차원의 vector가 된다.

이 score값은 결정 과정에서 model이 얼마나 confident한지 측정할 수 있는 지표이다.

score > 0 : model prediction = positive sample
score < 0 : model prediction = negative sample

+) margin
: $score * y$
→ $y = 1$ 이고 score값이 positive real 값이 경우 margin이 굉장히 커진다.
→ $y = -1$ 이고 score값이 negative real 값이 경우 margin이 굉장히 커진다.

score를 계산한 다음 그 출력에 sign 함수를 적용한다.

sign 함수 : 내부의 값 $< 0$ 이면 -1 출력 / 내부의 값 $≥ 0$ 이면 1 출력

2. model parameter를 fitting하기 위한 loss function은 어떻게 설정할 것인가?

→ linear regression은 MSE를 사용하지만,
classification은 zero-one loss, hinge loss, cross-entropy loss와 같은 함수를 사용한다.

$w$ 가 바뀜에 따라 샘플들의 판별 결과가 바뀌게 될텐데
그렇다면 Classification 문제에서는 error를 어떻게 판단할 수 있을까?

Zero-one loss
: 내부의 logic을 판별하여 맞으면 $0$ / 틀리면 $1$ 을 출력하는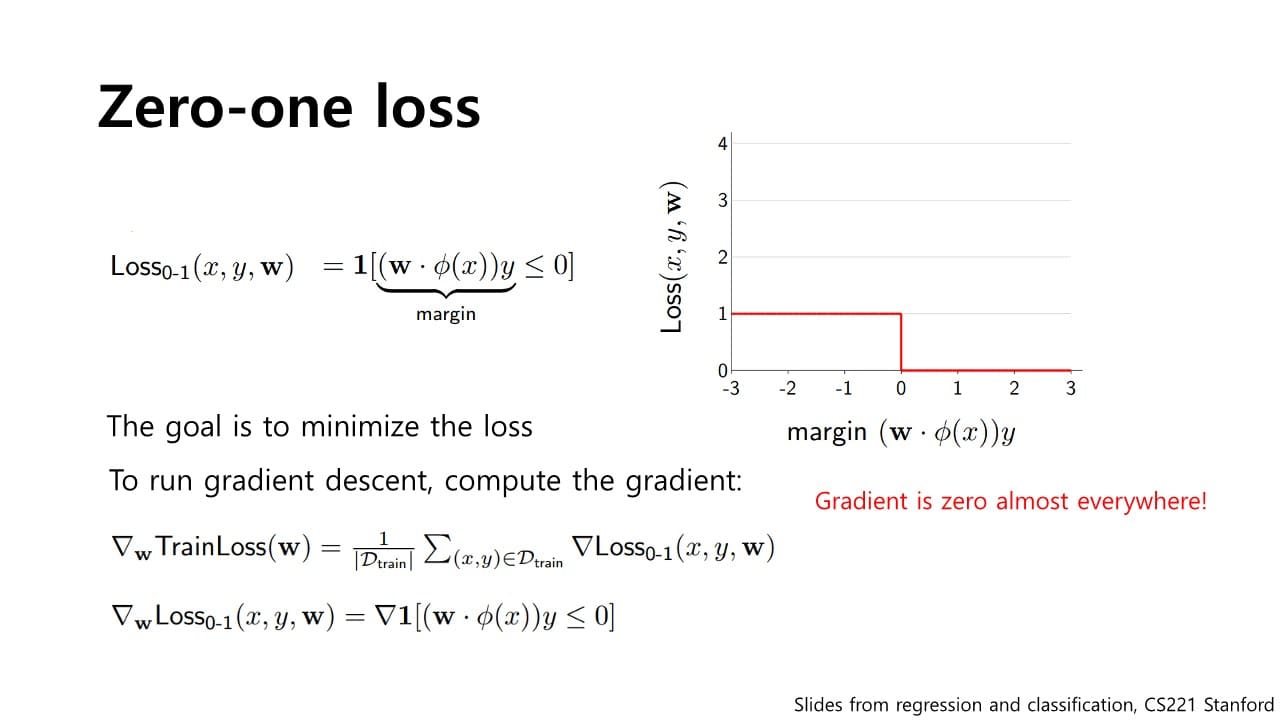 함수Zero-one loss를 경사하강법에 적용하기 위해서는 partial deritive term을 구해야 하는데 미분 시 gradient가 모두 0이 되는 문제가 발생한다. (= 학습 불가능)
Hinge loss
: $(1 - margin)$ 과 0 중 큰 값을 출력하는 함수Zero-one loss의 미분 시 문제점을 보완해준다.
Cross-entropy loss
: 두 개의 서로 다른 pmf를 가지는 $p$ 와 $q$ 가 서로 유사한지 / 그렇지 않은지의 정도에 따라 error가 바뀌는 함수두 개의 서로 다른 pmf를 가지는 확률 함수 사이의 가까운 정도 또는 서로 다른 정도를 특정하기 위한 KL divergence $D$ 에 의해 표현된다.
- $p$ 와 $q$ 가 서로 유사하다면 loss는 줄어들 것
- $p$ 와 $q$ 가 서로 굉장히 다르다면 loss는 증가할 것
  
  두 확률 간의 차이를 비교하는데,
  계산한 Score값은 어떻게 이러한 확률 값으로 Mapping할 수 있을까?
  → fitting을 하고자 하는 label은 0 또는 1이라는 값이 되는데
  score은 실수값이기 때문에 그 실수 값을 확률 함수를 통해 매핑해야 한다.
  ⇒ sigmoid 함수 사용
  sigmoid
  - (+) 방향으로 실수 값이 증가하게 된다면 확률 값은 1에 근사하게 될 것
  - (-) 방향으로 실수 값이 증가하게 된다면 확률 값은 0에 근사하게 될 것
  - 실수 값이 0이 된다면 확률 값은 $\frac{1}{2}$ 이 될 것
    
    ⇒ $h(x)$ 는 score값을 sigmoid 함수에 대입하여 실수 값을 0 ~ 1 사이의 값으로 매핑할 수 있다.
    $=$ logistic model