Module 3. 『지도학습(분류/회귀)』 5. Advanced Classification

📍 강의 자료 출처 : LG Aimers

overview

sample의 분류는 hyper plane을 기준으로 score값을 계산하여 classification을 수행한다.
이때 hyper plane을 구성하는 model paramter가 $w$이면,
이 hyper plane에 normal한 방향으로 hyper parameter $w$ vector를 구성하게 된다.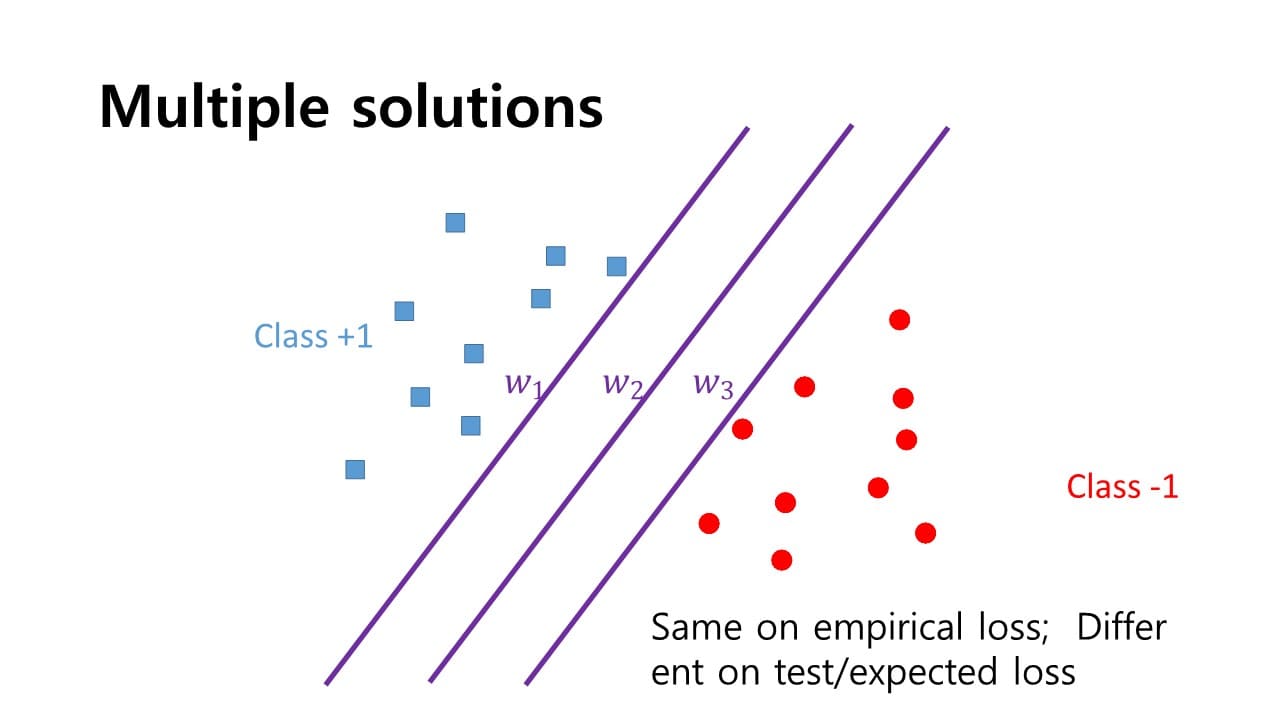같은 sample에 대해서도 다양한 경우의 수를 갖는 hyper plane이 존재하는데 각각은 서로 다른 성능을 제공할 것이다.
→ positive sample과 negative sample 중간 어딘가에 hyper plane을 긋는 것이 가장 최적이다.

---

positive sample과 negative sample 사이에 어떠한 방식으로 hyper plane를 그을 것인가?

SVM; Support Vector Machine

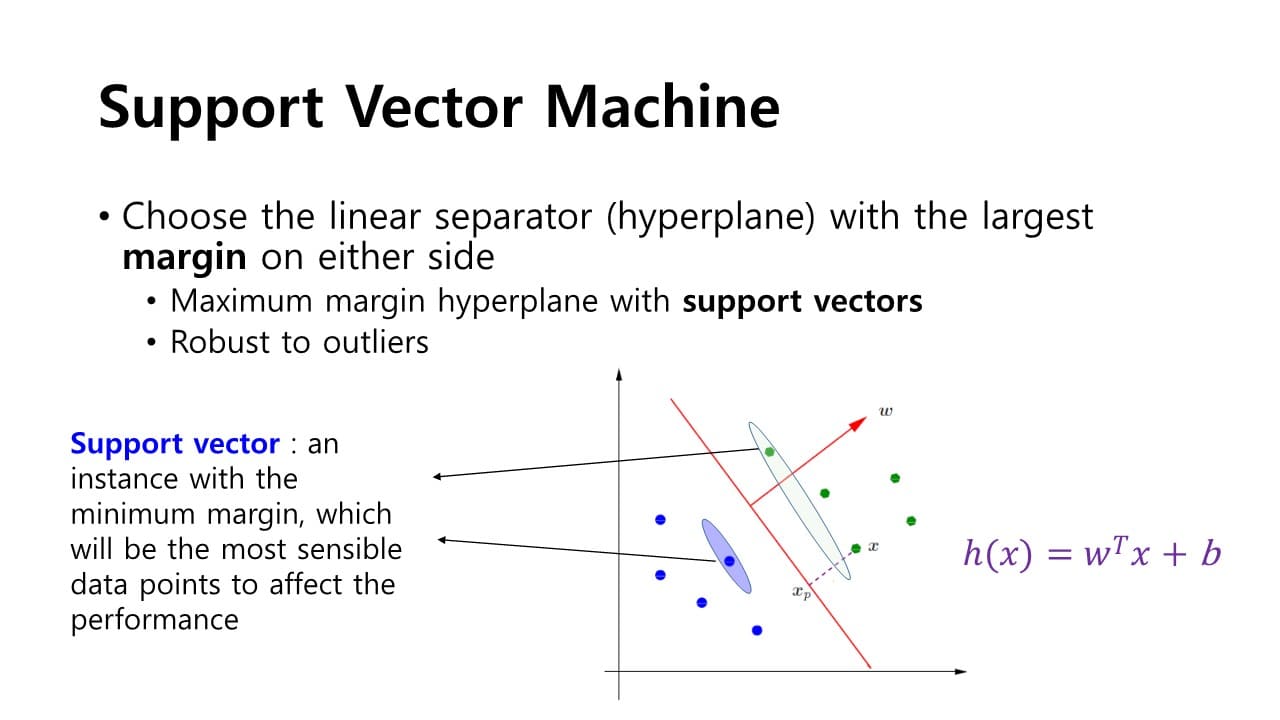: margin을 정의
positive sample에 가장 가깝게 지나는 점선과 negetive plane에 가장 가깝게 지나는 점선을 구하고 그 두 점선들의 중간에 있는 hyper plane이 최대 margin을 확보할 수 있는 최적화 방식이 된다.

장점

• 이상치가 발생해도 보다 안정적인 성능을 제공할 수 있다

supoort vector $x$
: positive sample들 중 hyper plane과의 거리가 가장 가까운 sample vector
&
negative sampel들 중 hyper plane과의 거리가 가장 가까운 sample vector
→ 성능을 좌지우지할 수 있는 민감한 데이터 포인트

→ 목표 : support vector간의 거리를 가장 최대화하는 Maximum margin을 설정하는 것

Margin은 어떻게 계산할 수 있을까?

SVM의 Optimization(최적화)

1. Hard margin SVM
   가정 : sample들의 linear separablility
   = hyper plane이 있고 각 support vector들을 연결하는 plane이 있을 때,
   그 사이 영역에는 어떠한 sample도 존재하지 않는다.

• constrained optimization
  

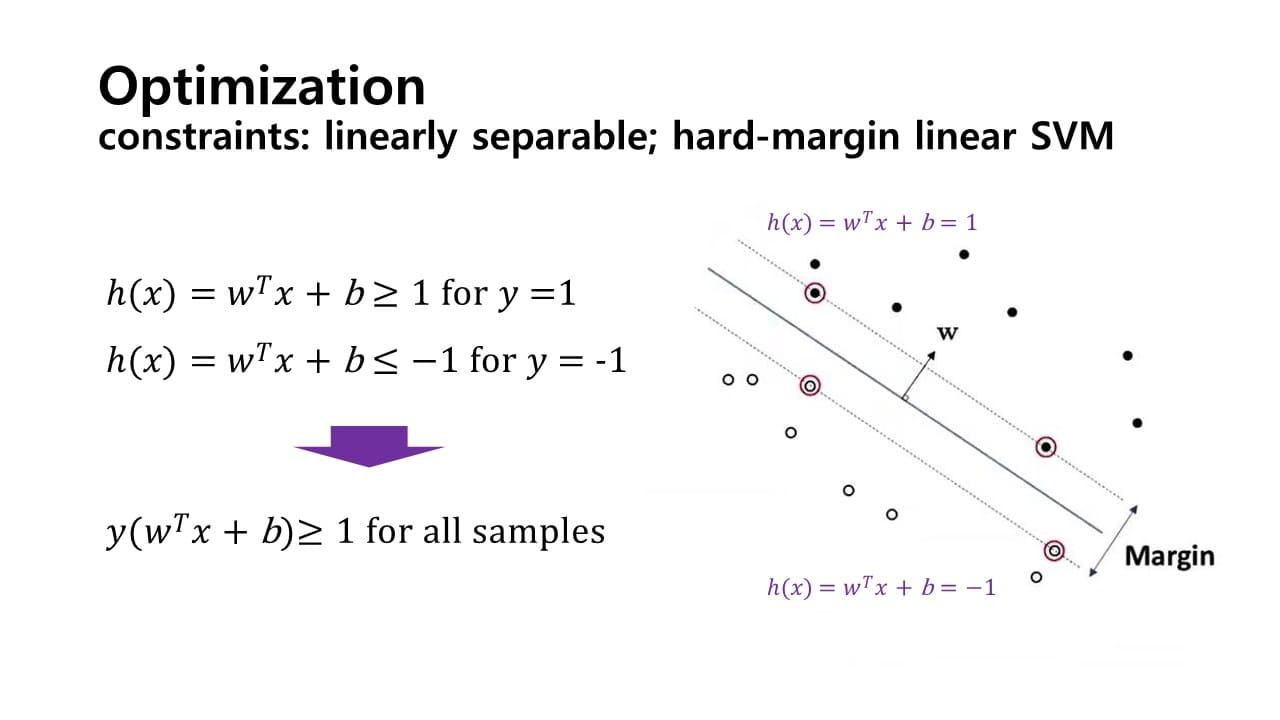
  • sampel이 positive(= 1) = $w^Tx + b ≥ 1$

  • sampel이 negative(= -1) = $w^Tx + b ≤ -1$

    → 제약 조건 : $y(w^T + b) ≥ 1$ for all samples

    hyper plane과 support vector 사이의 거리는 다음과 같이 구할 수 있다.
    $margin = \frac{w^Tx + b}{||w||}$ = $\frac{±1}{||w||}$

    우리의 목표는 margin을 최대화하는 것이기 때문에 분모인 $||w||$을 최소화하는 값을 구하면 SVM의 해를 구할 수 있다.

    ⇒ SVM의 Primal problem : margin을 최대화하기 위해 $w$의 norm을 최소화하는 값 구하기

2. Soft margin SVM
   어느 정도의 error를 용인하는 최적화 방식

3. Nonlinear transform & kernal trick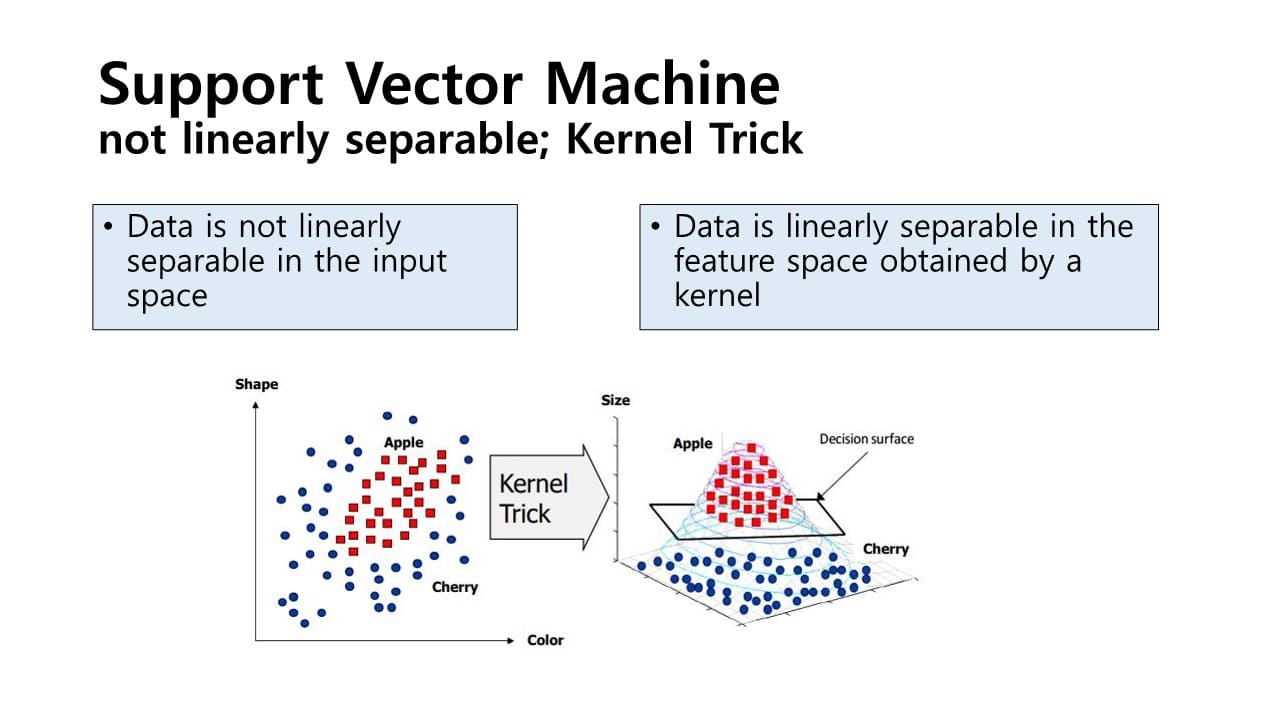: 2차원의 sample들을 보다 더 고차원의 sample들로 맵핑을 하는 함수를 이용하는 방식
   SVM이 linear한 경우에만 사용할 수 있다는 단점을 극복하기 위해 고안되었다.

   Optimization으로 SVM의 해를 구했는데,
   만약 데이터 sample들이 서로 linear sepable하지 않다면 앞서 설정했던 hyper plane을 통해 sample들을 구분할 수 없다.
   → kernal 함수를 통해 변환시켜 해를 구할 수 있다.

   Kernal 함수
   : Linearly sepable하지 않은 data sample들이 있다고 할 때,
   그 차수를 높여 linearly sepable하게 만드는 과정

   • Polynomial kernal
   • Gaussian redial basis function; RBF kernal
   • Hyperbolic tangent; multilayer perceptron kernal

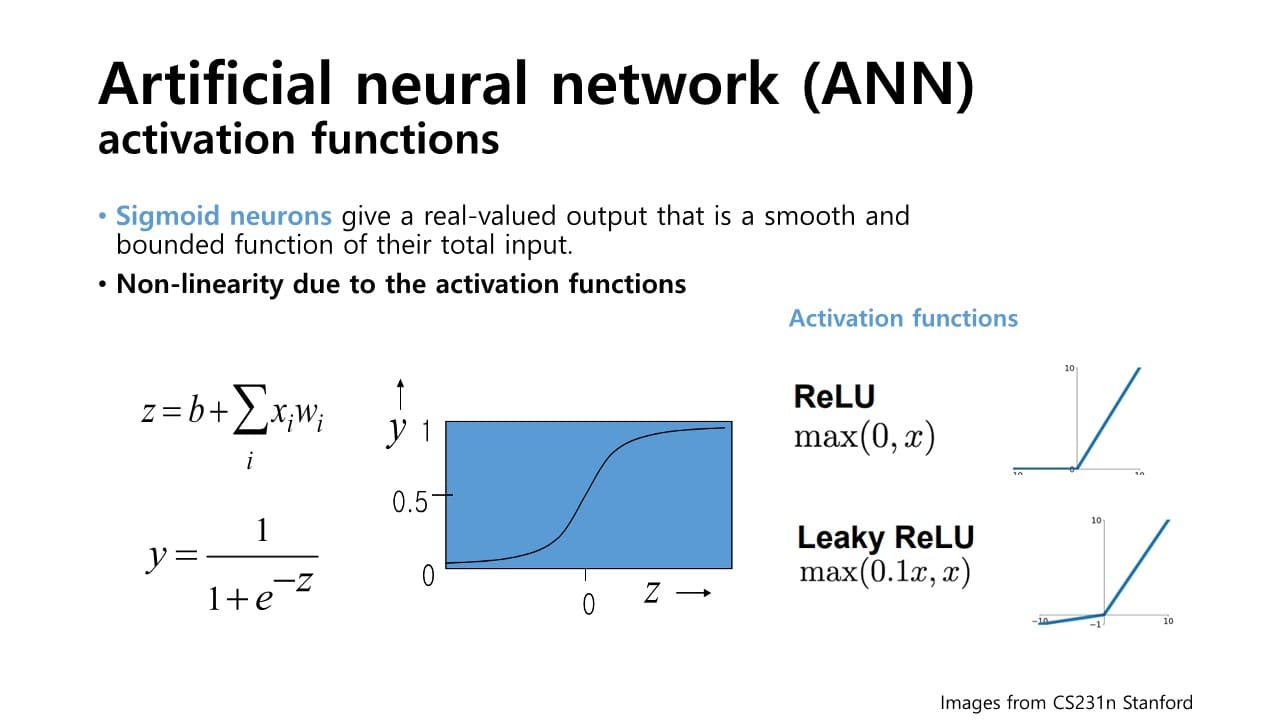
ANN; Artificial Neural Network

: Nonlinear Classification Model이자 Deep Neural Network의 기본이 되는 Model

Activation function에 의해 non-linear한 형태를 이루게 된다.

Activation function
: score를 입력으로 삼아 sigmoid와 같은 함수에 대입해 출력값을 non-linear하게 매핑해주는 역할

• sigmoid 함수
  : $z$가 너무 크거나 / 너무 작은 경우 미분값이 매우 작아짐
  → 학습량이 줄어들어 NN을 깊게 쌓아갈 때 효과적인 학습에 도움이 되지 않음
• ReLU
  : gradient term이 1로 유지되어 sigmoid의 문제점 보완

non-linear 함수들이 계층적으로 쌓여감에 따라 signal space에서의 복잡한 신호들의 패턴을 보다 정확하게 분류할 수 있게 된다.
예) XOR 문제 : 선형 모델로는 풀 수 없던 문제를 Multilayer Perceptron을 통해 해결

하지만 계층을 개수를 계속 늘리더라도 model 정확도가 어느순간 낮아지는 문제가 발생할 수 있다.
→ Gradient Vanishing Problem

Gradient Vanishing Problem
: 학습 parameter 업데이트할 때 chain rule을 이용하는데
계층이 깊어질수록 gradient값이 계속해서 줄어들게 된다.
→ 깊은 layer에 대해서는 학습이 효과적으로 진행되지 않는 문제

이러한 문제는 Back Propagation 시 pre-training + fine tuning을 거쳐 보완할 수 있다.