📍 강의 자료 출처 : LG Aimers
인과 효과 계산하기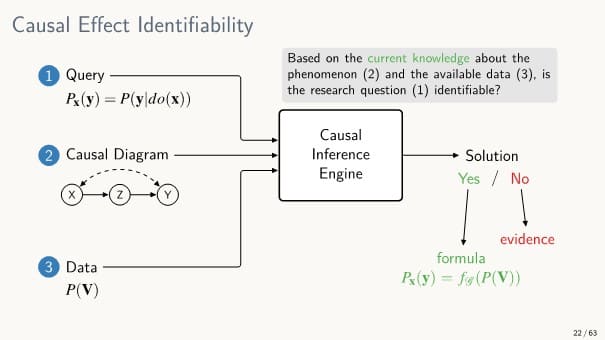


→ 결합 확률을 식으로 decompose해놓고 그 식에 가 나오는 확률을 1로 바꾸면, 중재 때의 확률 분포가 어떻게 될 것인가를 볼 수 있다.
지금까지는 식을 전개하고 그 결합 분포에서부터 중재하고 있는 변수, 그 변수와 관련된 조건부 확률을 제거하여 인과 효과를 계산하였다. 이러한 방식이 적용되기 위해서는 그래프의 모든 변수가 관측 가능해야 한다.
Back-door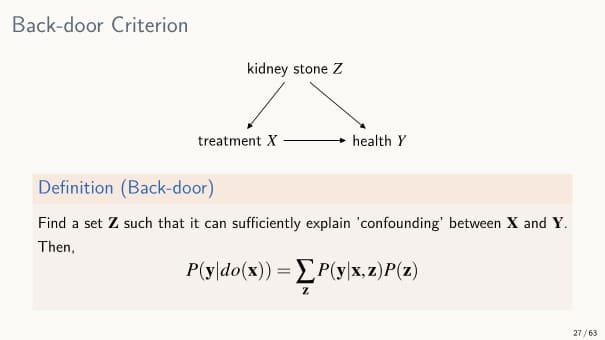
: 데이터에 나타나는 상관성에서 교란에 의한 상관성을 제고하고자 하는 방식
뒷문 조건에 부합하는 집합 는 2가지 조건을 만족해야 한다.
- 가 이후에 나타나는 변수이면 안된다.
→ 가 의 영향을 받으면 안된다. - 가 에서 로 연결되는 뒤로 가는 길목을 모두 막을 수 있어야 한다.

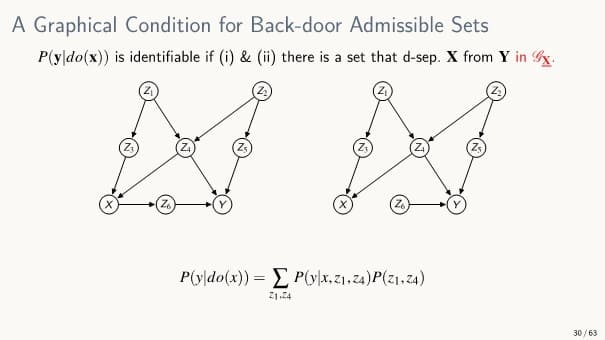
+) Back-door Criterion = Sound하다
+) Back-door Criterion을 통해 Formular는 찾을 수 있지만 모든 Formular를 찾을 수 있다고 보장하지 않는다
= Complete하지 않다
이러한 문제점을 해결하는 방법으로 Do-calculus가 고안되었다.
Do-calculus
: 여러 가지 다른 중재 조건에서 나오는 확률들끼리 서로 연결고리를 만들어주고
서로 다른 중재로 어떤 확률 분포를 바꿔주는 역할
Do-calculus는 3가지 룰을 가진다.
- 관찰에 대한 것이 추가되거나 삭제될 수 있다. (= 조건부 독립)
- Action과 Observation을 바꿀 수 있다.
- Action이 추가되거나 제거될 수 있다.
어떤 규칙에 의해 조건부 독립을 만족하는 경우를 찾는다면, 확률을 "다른 확률로 변경시킬 수 있다".
Back-door Criterion은 Sound하지만 Complete하진 않았는데
Do-calculus는 Sound하고 Complete하여 모든 Identifiable한 formular에 대해 인과 효과를 계산하는 식을 이끌어낼 수 있다.


