퍼셉트론 결정 함수
퍼셉트론의 결정 함수 :
임계값 theta기준으로 1과 -1로 사용
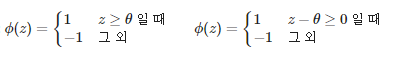
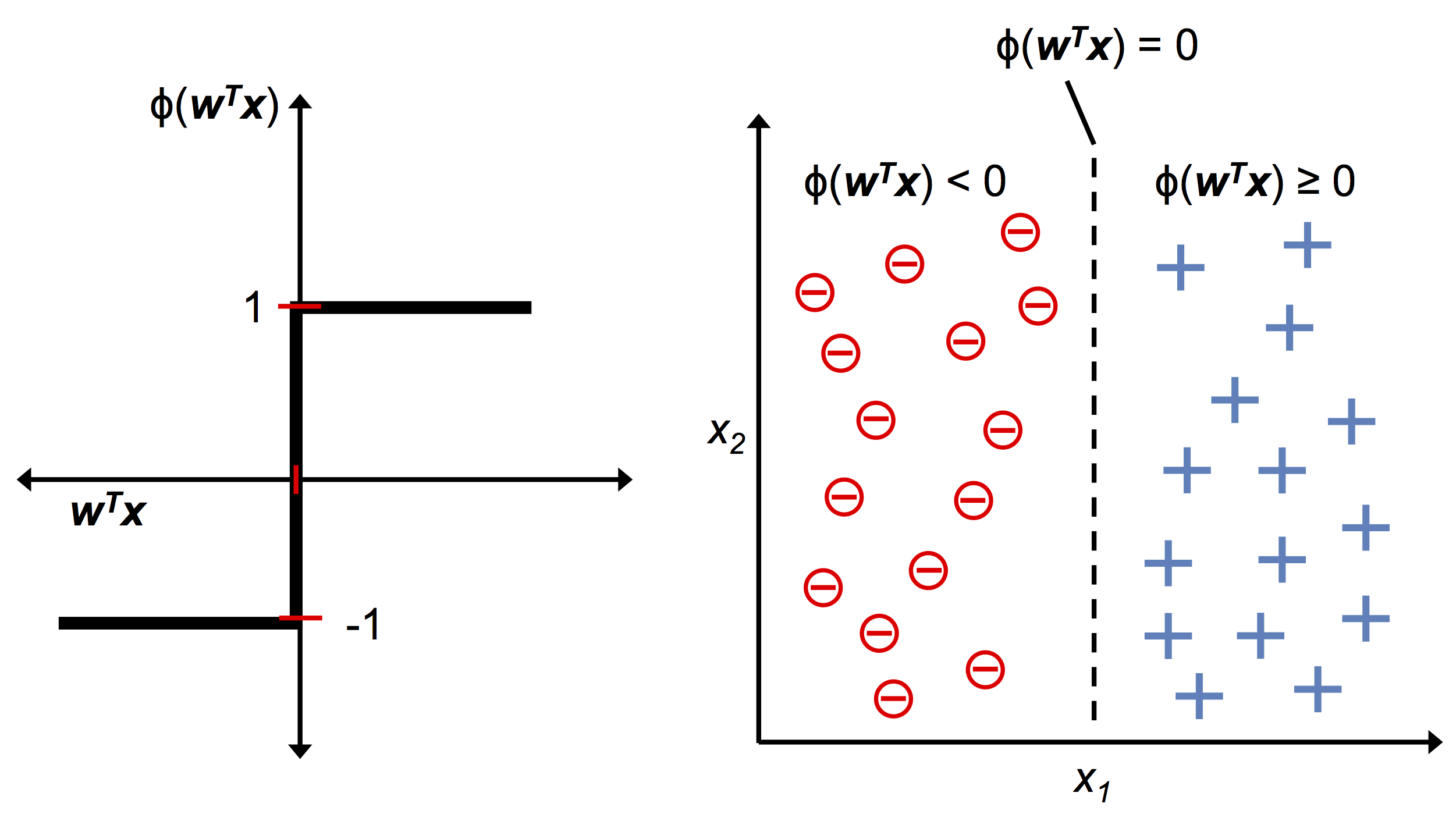
오른쪽 사진의 θ(w’x)=0가 결정경계로 양성/음성 클래스 나뉨
퍼셉트론 학습 규칙
w를 어떻게 찾냐에 따라서 결정경계가 달라짐. 좋은 w를 찾아야함 (다음장)
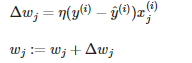
i번째 샘플의 타깃값(xi) η은 j번째 샘플의 특성(j번째 가중치) j번째 타깃값 y_i hat(y_i) 은 예측값,
타깃값에서 예측값을 빼서 x의 특성을 곱하고
△w_j (학습률) 계산한다.
퍼셉트론 부분 제대로 이해 안가서
https://liveyourit.tistory.com/63 이 블로그 참고해서 읽음
아무튼 퍼셉트론 특징은 결정함수 통과한 값(hatY) 을 이용해 오차 계산해 가중치 업데이트에 사용
적응형 선형 뉴런 (아달린)
요새 인공신경망에는 아달린 활성화 함수 사용- 임계함수 전에 출력값을 사용해서 다음 수를 업데이트함
아달린에서 활성함수는 입력값을 그대로 보낸다.
아달린의 활성화 함수 :Φ(z) = z
비용 함수 최소화 -경사 하강법
최적화 대상 함수 : 목적함수,
샘플하나 : 비용함수, 샘플 전체 : 손실 함수
용어 섞어서 사용
손실함수 보통 J(w) 로 나타낸다.
가중치가 하나라면 w 기울기 작아져서 기울기 0 이 된다. 초기 가중치 위치 상관없이 기울기(미분)으로 계산
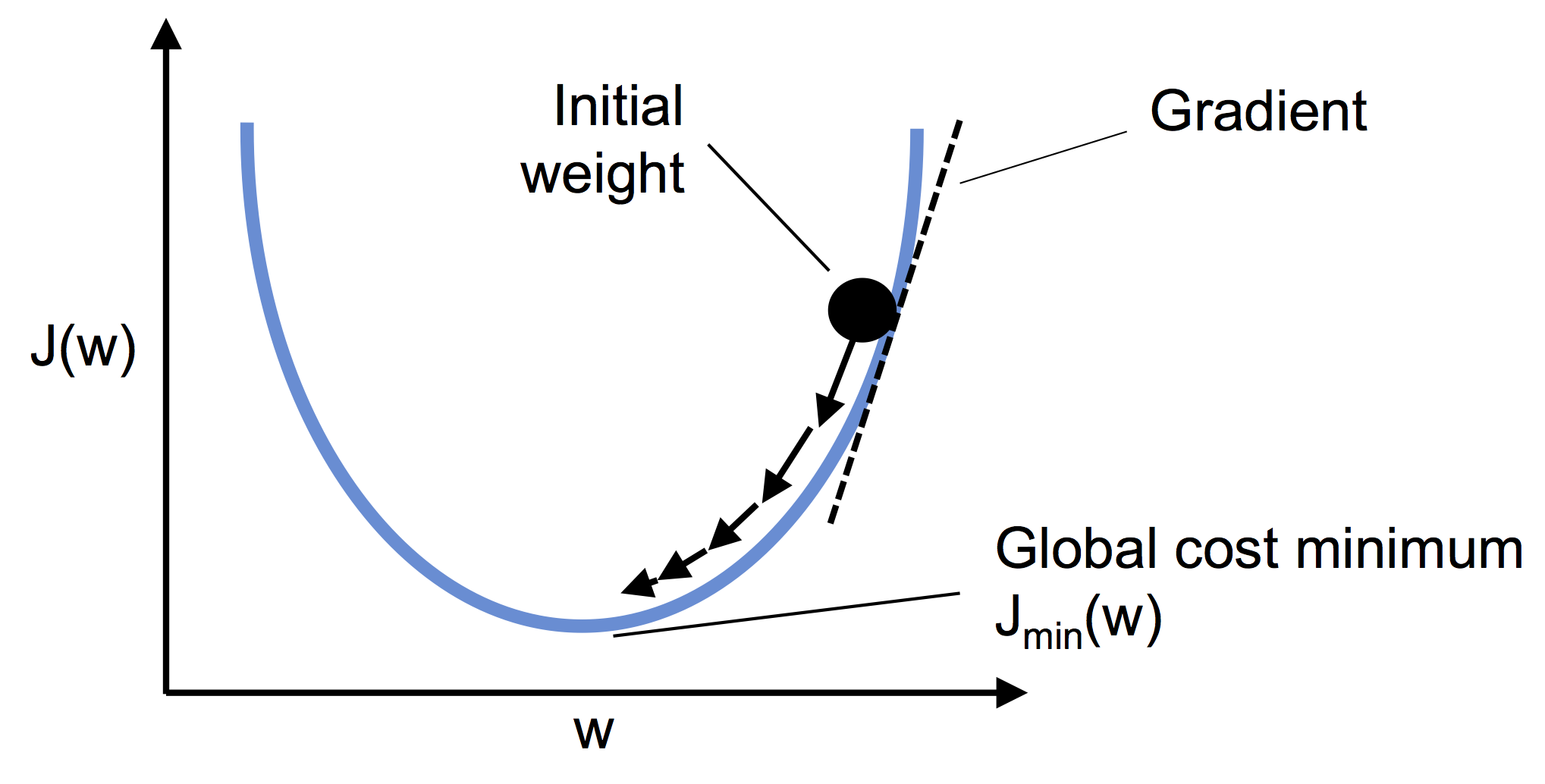
궁극적으로 비용최저점 : Global cost minimum에 도달.
w에 대해서 J(w)를 미분하면 된다.
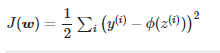
경사 하강법 결과 향상-특성 스케일을 조정
x 범위가 다르면 가중치마다 업데이트 범위가 달라짐. 업데이트 검증위해서 스케일 조정해야함.
표준화(z값) (standardization) :
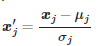
확률적 경사 하강법
앞에서 사용한 배치 경사하강법의 경우 너무 많은 샘플일 때 가중치 업데이트마다 sum이 너무 많음. 그래서 확률적 경사 하강법 사용.
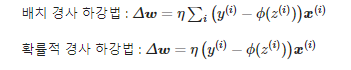
확률적 경사 하강법 : 샘플 하나 뽑을 때 전체에서 임의로 뽑아서 사용.
epoke마다 shuffle해서 무작위성 높여서 최저점 도달에 빠르게 가도록 한다.
sgd (확률) -> Batch GD (배치)
배치크기 1, 즉 샘플 1개로 업데이트 -> 전체 샘플 이용 업데이트 사이에 미니 배치 경사하강법 존재
신경망 알고리즘에서는 대부분 미니 배치 경사하강법 사용한다. (딥러닝)
공부 자료 : 머신 러닝 교과서 3판
원문 : https://github.com/rickiepark/python-machine-learning-book-3rd-edition/blob/master/ch01/ch01.ipynb
강의 : https://www.youtube.com/watch?v=WC4po1W4LzA&list=PLJN246lAkhQiEc-QvvGzUneCWuRnCNKgU