서포트 벡터 머신을 사용한 최대 마진 분류
🤨svm(Support Vector Machine)
: 퍼셉트론의 확장으로 생각 가능 , svm 최적화 대상은 마진을 최대화 하는 것.
-- 마진 : 클래스를 구분하는 결정경계와 이 경계에 가장 가까운 훈련 샘플 사이의 거리, 그리고 이 샘플을 서포트 벡터라고 함.
❓최대 마진의 결정 경계를 원하는 이유
: 일반화 오차가 낮아지는 경향 존재하기 때문, 작은 마진 모델은 과대적합 되기 쉽다.
결정 경계와 양성 샘플 쪽 초평면(결정경계)와 음성 샘플쪽을 식으로 써서 차이에서 벡터 w의 길이로 정규하고 나면
좌변은 양성 쪽 결정경게와 음성쪽 결정경계 사이의 거리로 해석 가능 -> 마진
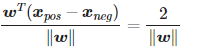
즉 우항 2/|w| 을 최대화해 마진을 최대화.
😁싸이킷럿의 LIBLINEAR와 LIBSVM 등의 라이브러리 존재. 순수한 파이썬 코드로 구현한 것에 비해 많은 선형 분류기 빠르게 훈련 가능하나 데이터셋 커서 메모리 용량 안맞는 경우 존재, 대안으로 SGDClassifier 클래스.
커널 SVM을 사용하여 비선형 문제해결
svm 인기 이유 중 하나는 비선형 문제 해결 위해 커널 방법 사용 가능하기 때문
😂커널 방법 for 선형적으로 구분되지 않는 데이터
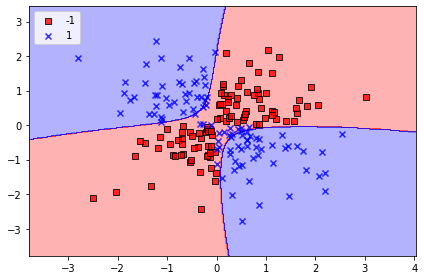
비선형 XOR데이터를 보면
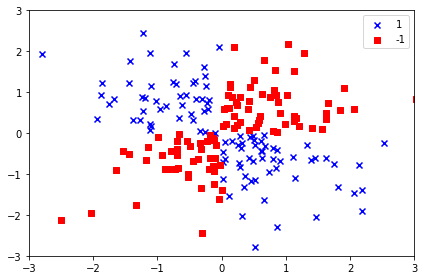
양성 클래스와 음성클래스를 선형 초평면으로 구분하기 어려움. 선형적으로 구분되지 않는 데이터를 다루는 커널방법의 기본 아이디어는 매핑 함수 Φ 이용해 원본 특성의 비선형 조합을 선형적으로 구분되는 고차원 공간에 투영하는 것
저차원에서는 찾을 수 없던 결정경계를 고차원 데이터에서는 찾을 수 있음.
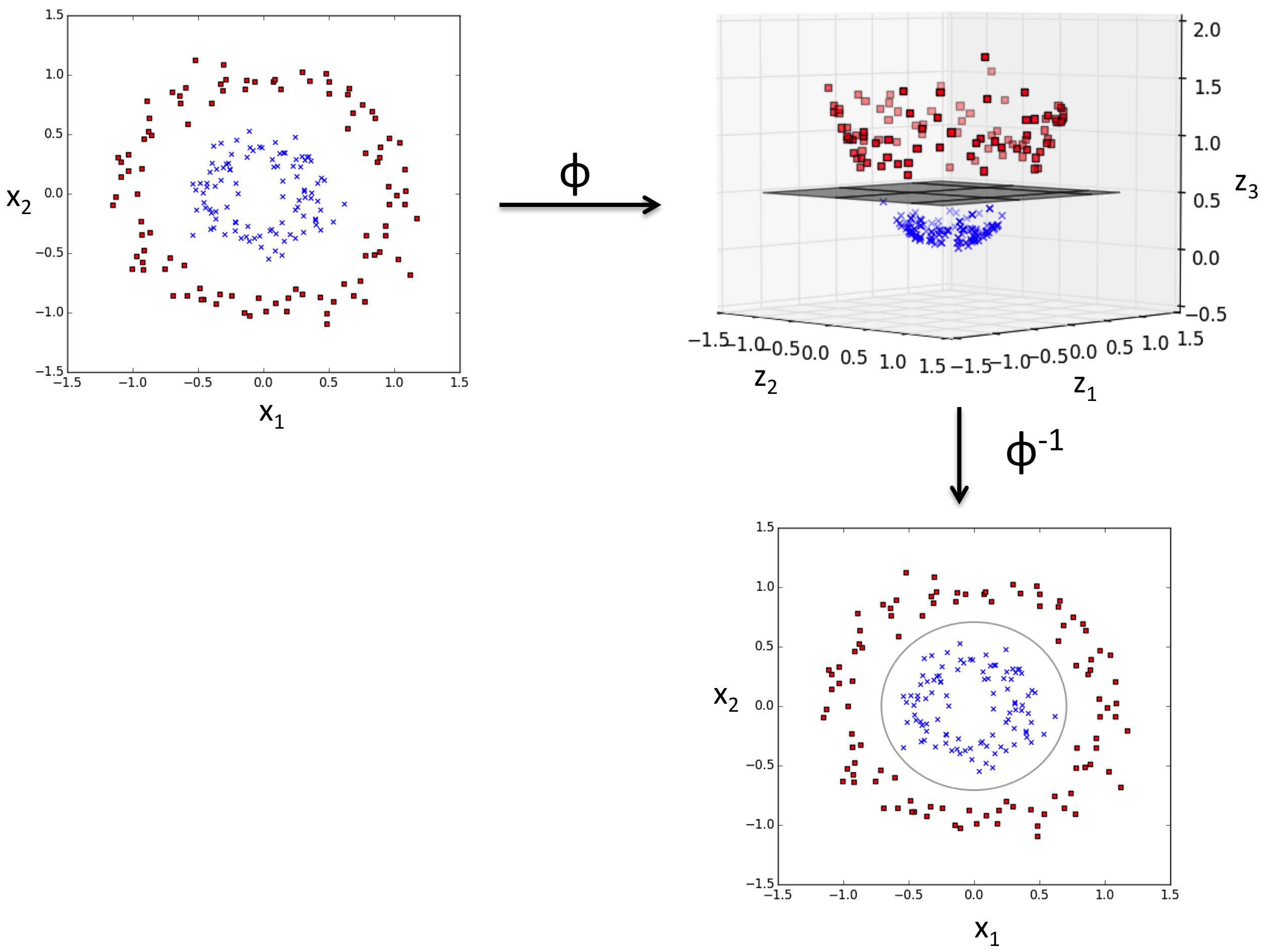
클래스들은 실제로 데이터들을 고차원 변환하는 것은 아니고 마치 고차원으로 표현한 듯한 효과를 내는 함수를 사용. 이런 함수를 커널 함수라 함.
커널 함수 중 가장 널리 사용되는 것은 방사 기저 함수(Radial Basis Function)
svm = SVC(kernel='rbf', random_state=1, gamma=0.10, C=10.0)
svm.fit(X_xor, y_xor)
plot_decision_regions(X_xor, y_xor,
classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('images/03_14.png', dpi=300)
plt.show()코드 실행 결과처럼, 커널 svm은 비교적 xor 데이터를 잘 구분하고 있음.
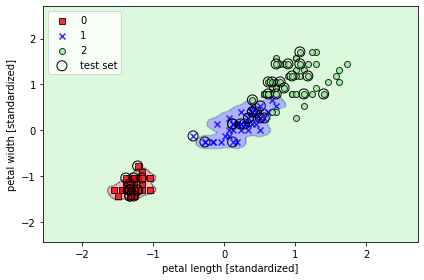
이전의 붓꽃 데이터에 SVM을 적용해보면
감마값이 0.2일때와
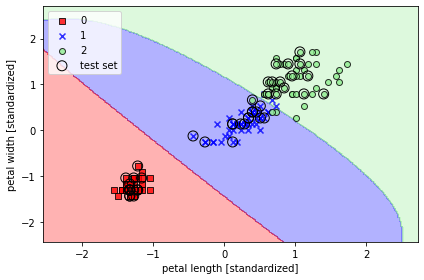
감마가 100일 때 (좀 많이 과대적합된 모델 ^^;; )