차원 축소를 사용한 데이터 압축
목차는
- 주성분 분석을 통한 비지도 차원 축소
- 선형 판별 분석을 통한 지도 방식의 데이터 압축
- 커널 PCA를 사용하여 비선형 매핑
로 이뤄진다.
비지도 차원 축소 by 주성분 분석 (PCA)
특성 선택과 마찬가지로 여러가지 특성 추출 기법을 사용해 데이터셋의 특성 개수 줄일 수 있음.
순차 후진 선택 -> 원본 특성 유지, 특성 추출은 새로운 특성 공간으로 데이터 변환하거나 투영
PCA는 특성 사이의 상관관계를 기반으로 하여 데이터에 있는 어떤 패턴을 찾을 수 있음. PCA는 고차원 데이터에서 분산이 가장 큰 방향을 찾고 좀 더 작거나 같은 수의 차원을 갖는 새로운 부분 공간으로 이를 투영
- 주성분 추출 단계
- 데이터 표준화 전처리
- 공분산 행렬 구성
- 공분산 행렬의 고유값과 고유 벡터 구함
- 고유값을 내림차순으로 정렬, 고유 벡터 순위 매김
70%는 훈련 세트로 30%는 테스트 세트로
from sklearn.model_selection import train_test_split
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.3,
stratify=y,
random_state=0)데이터 표준화
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)공분산 행렬의 고윳값 분해
import numpy as np
cov_mat = np.cov(X_train_std.T)
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
print('\n고윳값 \n%s' % eigen_vals)이 결과 출력된
고윳값
[4.84274532 2.41602459 1.54845825 0.96120438 0.84166161 0.6620634
0.51828472 0.34650377 0.3131368 0.10754642 0.21357215 0.15362835
0.1808613 ]
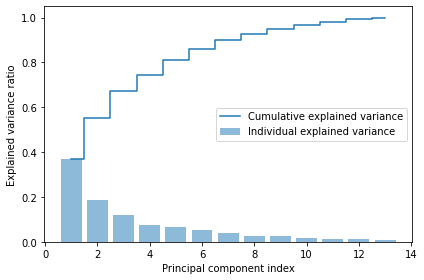
이 설명된 분산 비율이다.
데이터셋 차원을 새로운 특성 부분 공간으로 압축하여 줄여야하기 때문에 가장 많은 정보(분산)가진 고유 벡터(주성분) 일부만 선택 ->그래서 내림차순 정렬
특성 변환
공분산 행렬을 고유 벡터와 고유값 쌍으로 성공적 분해 후
Wine 데이터셋을 새로운 주석분 축으로 변환하기 위해선
1. 고유값 가장 큰 k개 고유 벡터 선택 (k는 새 특성 부분 공간 차원)
2. 최상위 k개 고유벡터 투영 행렬 W만듦
3. 투영 행렬 사용, d 차원 입력데이터셋 X를 새로운 k차원 특성 부분 공간으로 변환
이 예제에서는 2차원 산점도 그리기 위해 두개의 고유벡터만 선택했음. 실전에서는 계산 효율성과 모델 성능사이 절충점 찾아 주성분 개수 결정 필요!
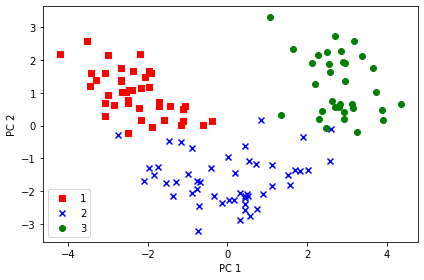
그래서 124*2 차원 헹렬의 Wine 훈련 데이터셋 2차원 plot그리면
두개의 특성으로 줄어든 거 확인 가능
데이터가 y축보다 x축 따라 더 넓게 퍼져있음.
선형 분류기가 클래스들을 잘 분리할 수 있ㅇ르 것 같다고 직관적으로 알 수 있음.
사이킷 런 주성분 분석
사이킷런 PCA 클래스
from sklearn.decomposition import PCA
pca에 매개변수 안주면 13개의 주성분 모두다 찾는다.
그러므로 X_train_std 넣어줘야함
from sklearn.decomposition import PCA
pca = PCA()
X_train_pca = pca.fit_transform(X_train_std)
pca.explained_variance_ratio_n_components=2 로 주성분 두개만 찾도록 함
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)싸이킷런은 고유값 분해 방식 안사용하고 SVD를 이용해서 PCA한다.
결과 산점도는 두 방법 모두 비슷하게 나옴
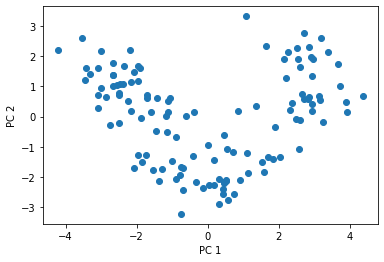
처음 두 개의 주성분을 사용하여 로지스틱 회귀 분류기를 훈련
from sklearn.linear_model import LogisticRegression
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)
lr = LogisticRegression(random_state=1)
lr = lr.fit(X_train_pca, y_train)훈련세트 세 개 클래스 잘 나누고 있음
plot_decision_regions(X_train_pca, y_train, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
# plt.savefig('images/05_04.png', dpi=300)
plt.show()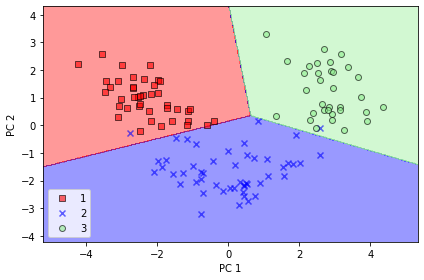
테스트 세트 봐도 약간 오차 있지만 그래도 꽤 분류한 결과 나옴
plot_decision_regions(X_test_pca, y_test, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
# plt.savefig('images/05_05.png', dpi=300)
plt.show()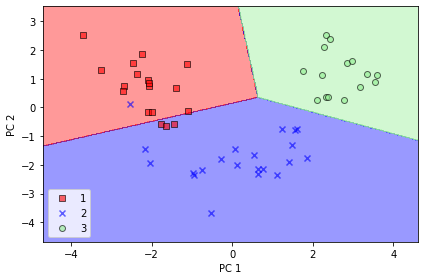
전체 주성분의 설명된 분산 비율 알고싶다면 n_components=None을 지정하고 PCA클래스 객체 만들면 된다.
pca = PCA(n_components=None)
X_train_pca = pca.fit_transform(X_train_std)
pca.explained_variance_ratio_의 출력 결과
array([0.36951469, 0.18434927, 0.11815159, 0.07334252, 0.06422108,
0.05051724, 0.03954654, 0.02643918, 0.02389319, 0.01629614,
0.01380021, 0.01172226, 0.00820609])