지도 방식의 데이터 압축 by 선형 판별 분석
LDA(선형 판별 분석 )은 규제가 없는 모델에서 차원의 저주로 인한 과대 적합 정도를 줄이고 계산 효율성을 높이기 위한 특성 추출의 기법으로 사용 가능
PCA가 데이터셋에 있는 분산이 최대인 직교 성분 축을 찾으려고하는 반면, LDA목표는 클래스 최적 구분할 수 있는 특성 부분 공간 찾는 것.
주성분 분석Vs 선형 판별 분석
PCA vs LDA
모두 데이터셋 차원 개수 줄이는 선형 변환 기법.
PCA는 비지도 학습 알고리즘
LDA는 지도학습 알고리즘, 분류작업에서 더 뛰어난 특성 추출 기법
선형 판별 분석의 내부 동작 방식

사이킷런의 LDA
사이킷런 구현 LDA 클래스
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
이용해서 사용
LDA로 변환 저차원 훈련 데이터셋
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components=2)
X_train_lda = lda.fit_transform(X_train_std, y_train)데이터셋에 로지스틱 회귀 분류기가 잘 동작하는지 확인
(LogisticRegression)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(random_state=1)
lr = lr.fit(X_train_lda, y_train)
plot_decision_regions(X_train_lda, y_train, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()plot 클래스 2의 샘플 하나가 로지스틱 회위 모형의 결정 경계에 가까이 놓여있음
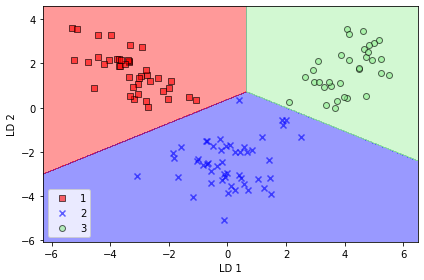
규제 강도 낮춰서(lda.transform) 로지스틱 회귀 모델이 훈련 데이터셋의 모든 샘플을 더 확실하게 분류하도록 결정 경계 옮기기
X_test_lda = lda.transform(X_test_std)
plot_decision_regions(X_test_lda, y_test, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
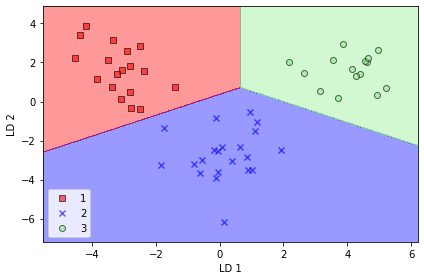
plt.show()다음 plot처럼 로지스틱 회귀 분류기는 원본 13개의 wine 특성 대신 2차원의 특성 부분 공간을 사용해 테스트 데이터셋에 있는 모든 샘플 잘 분류
비선형 매핑 by 커널 PCA
많은 머신러닝 알고리즘은 입력 데이터가 선형적 구분 가능하다는 가정으로 하는데, 퍼셉트론은 수렴하기 위해 훈련 데이터가 선형적으로 완벽 분리 가능해야한다고 배웠음.
지금까지 선형적 완벽 분리 안되느 이유 잡음때문이라고 가정함 .
실전에선 비선형 문제 더 자주 맞닥뜨림
비선형에는 PCA나 LDA같은 차원축서 위한 선형 변호나 기법이 최선 아님
커널 PCA 사용해 선형적으로 구분되지 않는 데이터 선형 분류기에 적합한 새로운 저차원 부분 공간으로 변환할 것
왼쪽 사진이 선형 문제 오른쪽이 비선형 문제
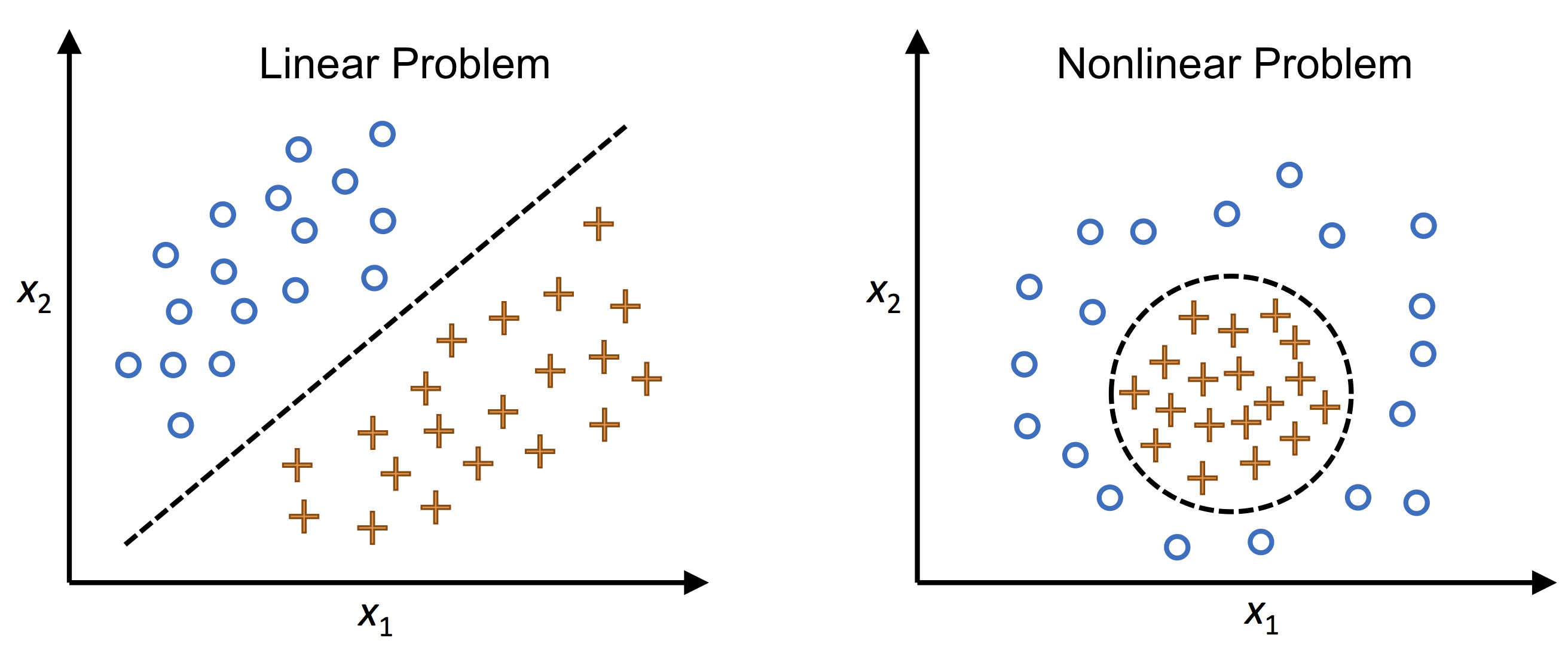
3장 커널 SVM 떠올리면 비선형 문제 해결위해 클래스가 선형으로 구분되는 새로운 고차원 특성 공간으로 투영.
커널 PCA를 통한 비선형 매핑을 수행하여 데이터를 고차원 공간으로 변환, 고차원 공간에 표준 PCA 사용해 샘플이 선형 분류기로 구분될 수 있는 저차원 공간으로 데이터 투영. -> 비용多 -> 커널 트릭 등장 (kernel trick)
커널 트릭 사용해 원본 특성 공간에서 두 고차원 특성 벡터 유사도 계산 가능
커널 PCA로 얻은 것은 표준 pca 방식처럼 투영행렬 구성한게 아니고 각각의 성분에 이미 투영된 샘플. 기본적으로 커널 함순느 두 벡터의 점곱을 계싼할 수 있는 함수 (=유사도 측정할 수 있는 함수)
파이썬으로 커널 PCA 구현
반달 데이터셋은 선형적 구분 안됨.
목표는 커널 PCA로 반달 모양 펼쳐서 선형 분류기에 적합한 입력 데이터셋으로 만드는 것
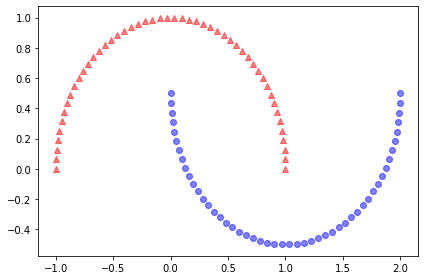
기본 PCA 변환된 데이터셋을 보면 선형 분류기가 잘 구분 못할 것 같음
카널 PCA함수 rbf_kernel_pca
- 구현
from scipy.spatial.distance import pdist, squareform
from scipy.linalg import eigh
import numpy as np
from distutils.version import LooseVersion as Version
from scipy import __version__ as scipy_version
# scipy 2.0.0에서 삭제될 예정이므로 대신 numpy.exp를 사용합니다.
if scipy_version >= Version('1.4.1'):
from numpy import exp
else:
from scipy import exp
def rbf_kernel_pca(X, gamma, n_components):
"""
RBF 커널 PCA 구현
매개변수
------------
X: {넘파이 ndarray}, shape = [n_samples, n_features]
gamma: float
RBF 커널 튜닝 매개변수
n_components: int
반환할 주성분 개수
반환값
------------
X_pc: {넘파이 ndarray}, shape = [n_samples, k_features]
투영된 데이터셋
"""
# MxN 차원의 데이터셋에서 샘플 간의 유클리디안 거리의 제곱을 계산합니다.
sq_dists = pdist(X, 'sqeuclidean')
# 샘플 간의 거리를 정방 대칭 행렬로 변환합니다.
mat_sq_dists = squareform(sq_dists)
# 커널 행렬을 계산합니다.
K = exp(-gamma * mat_sq_dists)
# 커널 행렬을 중앙에 맞춥니다.
N = K.shape[0]
one_n = np.ones((N, N)) / N
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
# 중앙에 맞춰진 커널 행렬의 고윳값과 고유벡터를 구합니다.
# scipy.linalg.eigh 함수는 오름차순으로 반환합니다.
eigvals, eigvecs = eigh(K)
eigvals, eigvecs = eigvals[::-1], eigvecs[:, ::-1]
# 최상위 k 개의 고유벡터를 선택합니다(결과값은 투영된 샘플입니다).
X_pc = np.column_stack([eigvecs[:, i]
for i in range(n_components)])
return X_pc적용
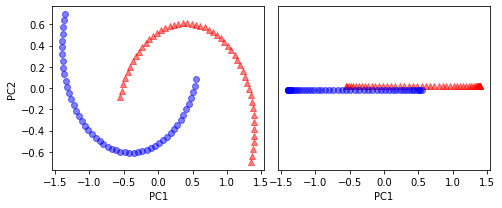
X_kpca = rbf_kernel_pca(X, gamma=15, n_components=2)
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7, 3))
ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_kpca[y==0, 0], np.zeros((50, 1))+0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_kpca[y==1, 0], np.zeros((50, 1))-0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
# plt.savefig('images/05_14.png', dpi=300)
plt.show()하게 되면 두 클래스는 선형적 구분 잘 되므로 선형 분류기 위한 훈련 데이터로 적합함.
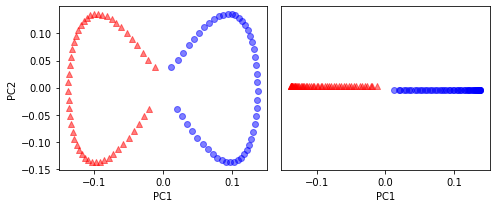
사이킷런의 커널 PCA
from sklearn.decomposition import KernelPCA 을 이용해서 커널 PCA클래스 이용가능.
kernel 매개변수로 커널의 종류 지정
from sklearn.decomposition import KernelPCA
X, y = make_moons(n_samples=100, random_state=123)
scikit_kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_skernpca = scikit_kpca.fit_transform(X)
plt.scatter(X_skernpca[y == 0, 0], X_skernpca[y == 0, 1],
color='red', marker='^', alpha=0.5)
plt.scatter(X_skernpca[y == 1, 0], X_skernpca[y == 1, 1],
color='blue', marker='o', alpha=0.5)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.tight_layout()
# plt.savefig('images/05_19.png', dpi=300)
plt.show()출력은 아까의 반달 모양 데이터 (처음 두개의 주성분 )
사이킷런의 매니폴드 알고리즘을 반달 모양 데이터셋과 동심원 데이터셋에 적용위해
-- 변환된 2차원 데이터셋 그래프 그리기 위한 함수
def plot_manifold(X, y, savefig_name):
plt.scatter(X[y == 0, 0], X[y == 0, 1],
color='red', marker='^', alpha=0.5)
plt.scatter(X[y == 1, 0], X[y == 1, 1],
color='blue', marker='o', alpha=0.5)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.tight_layout()
# plt.savefig(savefig_name, dpi=300)
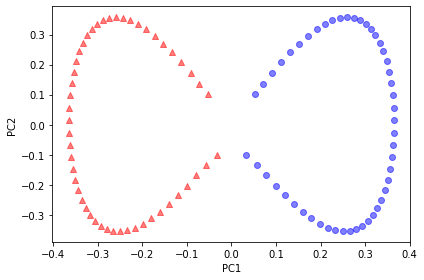
plt.show()지역 선형 임베딩(이웃한 샘플 간의 거리를 유지하는 저차원 투영을 찾음)
반달 모양은 유지되지 않았지만 두 클래스 뚜렷하게 구분되었음
from sklearn.manifold import LocallyLinearEmbedding
lle = LocallyLinearEmbedding(n_components=2, random_state=1)
X_lle = lle.fit_transform(X)
plot_manifold(X_lle, y, 'images/05_lle_moon.png')
같은 데이터셋에 t-SNE 알고리즘 적용해보면 두 클래스 선형적 구분할 수 있을 정도로 잘 분리했고 원래 반달 모양도 어느정도 유지함
**t-SNE 알고리즘 : (데이터 포인트 간의 유사도를 결합 확률(joint probability)로 변환하고, 저차원과 고차원의 확률 사이에서 쿨백-라이블러(Kullback-Leibler) 발산을 최소화)
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, random_state=1)
X_tsne = tsne.fit_transform(X)
plot_manifold(X_tsne, y, 'images/05_tsne_moon.png')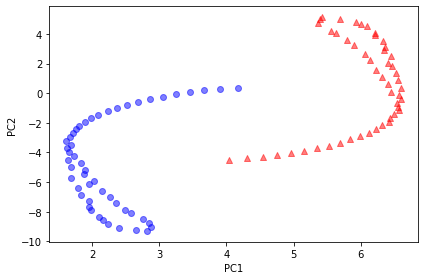
KernelPCA, LocallyLinearEmbedding, TSNE 를 동심원 데이터셋에 적용시키면 앞 서 구현한 rbf_kernel_pca와 거의 같은 결과 나옴
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1000, random_state=123, noise=0.1, factor=0.2)
scikit_kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_skernpca = scikit_kpca.fit_transform(X)
plot_manifold(X_skernpca, y, 'images/05_kpca_circles.png')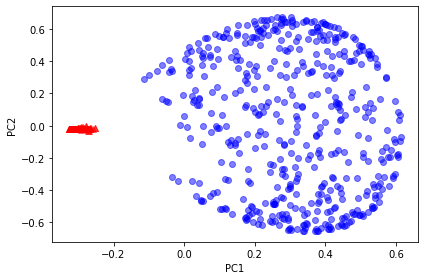
이번엔 지역 선형 임베딩 적용해보면
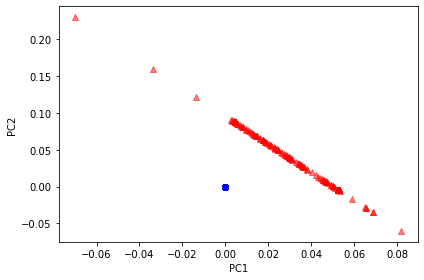
결과 나온다. 마지막으로 t-SNE 적용하면 선형적으로 두 동심원 완벽 분리했을 뿐 아니라 모양도 거의 보존하고 있다.