모델 평가와 하이퍼파라미터 튜닝
이번 장은 알고리즘 미세 조정하여 높은 성능의 머신러닝 모델 만들고 성능 평가 방법 배움
- 머신러닝 모델 성능 평가하고
- 머신러닝 알고리즘 일반적 발생 문제 분석하고
- 머신러닝 모델 세부 튜닝하고
- 여러가지 성능 지표 사용해 모델 예측 서응 평가할 것임
효과적 워크플로 by 파이프라인
이전 장에서는 여러 전처리 기법 적용했었음. 4장은 특성 스케일 조정위해 표준화, 5장은 데이터 압축 위해 주성분 분석 사용했음.
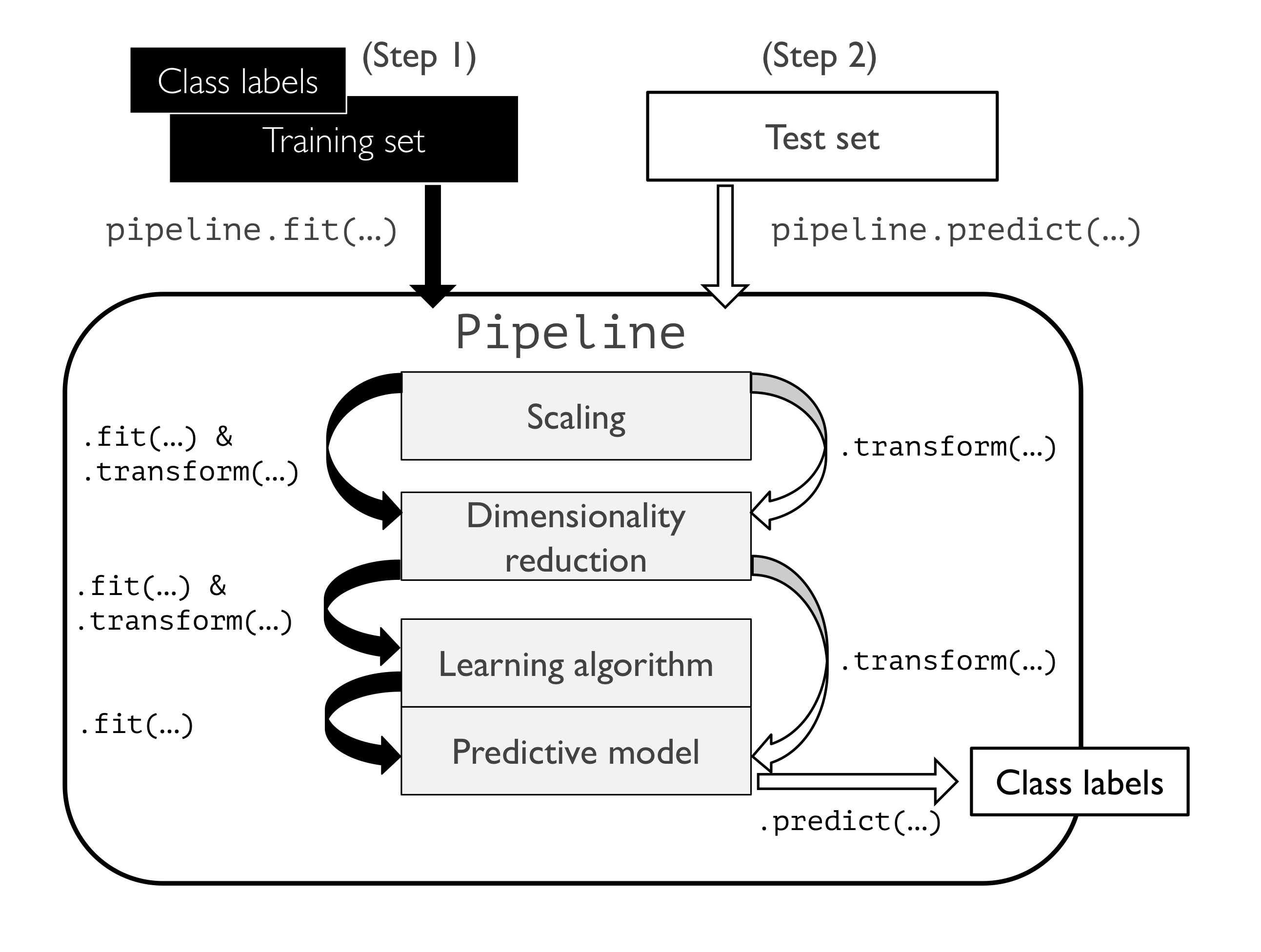
테스트 데이터셋에 있는 별도의 샘플처럼 새로운 데이터 스케일 조정하고 압축하기 위해 훈련 데이터셋에서 학습한 파라미터 재사용한다고 배웠는데 이를 위해 사이킷런의 Pipeline 클래스를 배울 것임 -> 여러개의 변환 단계를 포함한 모델 학습하고 새로운 데이터에 대한 예측 만들 수 있음
위스콘신 유방암 데이터셋
악성과 양성 세포 샘플 569개
세포 핵의 디지털 이미지에서 계산된 실수 값 특성 이용해 종양이 악성인지 양성인지 예측하는 모델 만들 것임.
데이터셋 읽고 정수 변환해 넘파이 배열 X에 할당하고 클래스 케이블을 배열 y에 인코딩하고 매핑해 훈련80와 테스트 20로 나눔
import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases'
'/breast-cancer-wisconsin/wdbc.data', header=None)
from sklearn.preprocessing import LabelEncoder
X = df.loc[:, 2:].values
y = df.loc[:, 1].values
le = LabelEncoder()
y = le.fit_transform(y)
le.classes_
le.transform(['M', 'B'])
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = \
train_test_split(X, y,
test_size=0.20,
stratify=y,
random_state=1)이제 최적 성능 위해 알고리즘 입력 특성이 같은 스케일 가져야한다는 것을 바탕으로 로지스틱 회귀 같은 선형 분류기에 주입하기 전에 특성 표준화를 시켜준다.
여기선 주성분 분석 통해 초기 30차원에서 2차원 부분공간으로 데이터 압축 가정.
훈련 데이터셋과 테스트 데이터셋 각각 학습/변환 단게 구성 대신 StandardScaler,PCA, LogisticRegression를 하나의 파이프라인으로 연결 가능
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
pipe_lr = make_pipeline(StandardScaler(),
PCA(n_components=2),
LogisticRegression(random_state=1))
pipe_lr.fit(X_train, y_train)
y_pred = pipe_lr.predict(X_test)PipeLine 객체의 fit 메서드 호출하면 데이터가 중간 단계에 있는 모든 변환기의 fit메서드와 transform메서드를 차례로 거쳐 추정기 객체에 도달한다.
추정기는 변환된 훈련 데이터셋을 사용하여 학습한다.
PipeLine 객체는 predict 메서드도 제공하는데, 메소드 호출 시 주입된 데이터는 중간 단계 transform 메소드 통과해 마지막 단계에서 추정기 객체가 변환된 데이터에 대한 예측 반환한다.
나중 뒷 부분에서도 파이프라인 자주 사용할거라 파이프라인 작동 방식 그림 잘 이해해두기
모델 성능 평가 by k-겹 교차 검증
모델이 너무 간단하면 과소적합(높은 편향)이 문제가 되고 너무 복잡하면 과대적합(높은 분산)이 될 수있음. (3장에서 봤던 것처럼 )
적절한 편향-분산 trade off 찾으려면 모델 주의 깊게 평가 필요
이 절에서는 보편적 교차 검증 기법인 홀드아웃 교차 검증과 k겹 교차검증 배울 것
-> 모델의 일반화 성능 추정 하도록 도움 (처음 본 데이터에 모델이 얼마나 잘 동작하는지 신뢰할 만한 추정)
홀드아웃 방법
초기 데이터셋을 별도의 훈련 데이터셋과 테스트 데이터셋으로 나눔. 전자는 모델 훈련에 사용, 후자는 일반화 성능 추정에 사용
- 모델 선택 : 처음 본 데이터에서 예측 성능 높이기 위해 하이퍼파라미터 튜닝하고 비교
모델 선택에 같은 테스트 데이터셋 반복 재사용 시 훈련 데이터셋의 일부되고, 모델 과대적합된다.
홀드아웃 방법 중 좋은 방법은
데이터를 훈련 데이터셋, 검증 데이터셋, 테스트 데이터셋 세 개의 부분으로 나누는 것
훈련 - 모델 훈련
-> 검증 - 모델 선택에 사용, 반복적으로 다른 파라미터 값에서 모델 훈련 후 성능 평가, 만족할만한 하이퍼파라미터 값 얻으면
-> 테스트 데이터셋에서 모델 일반화 성능 추정
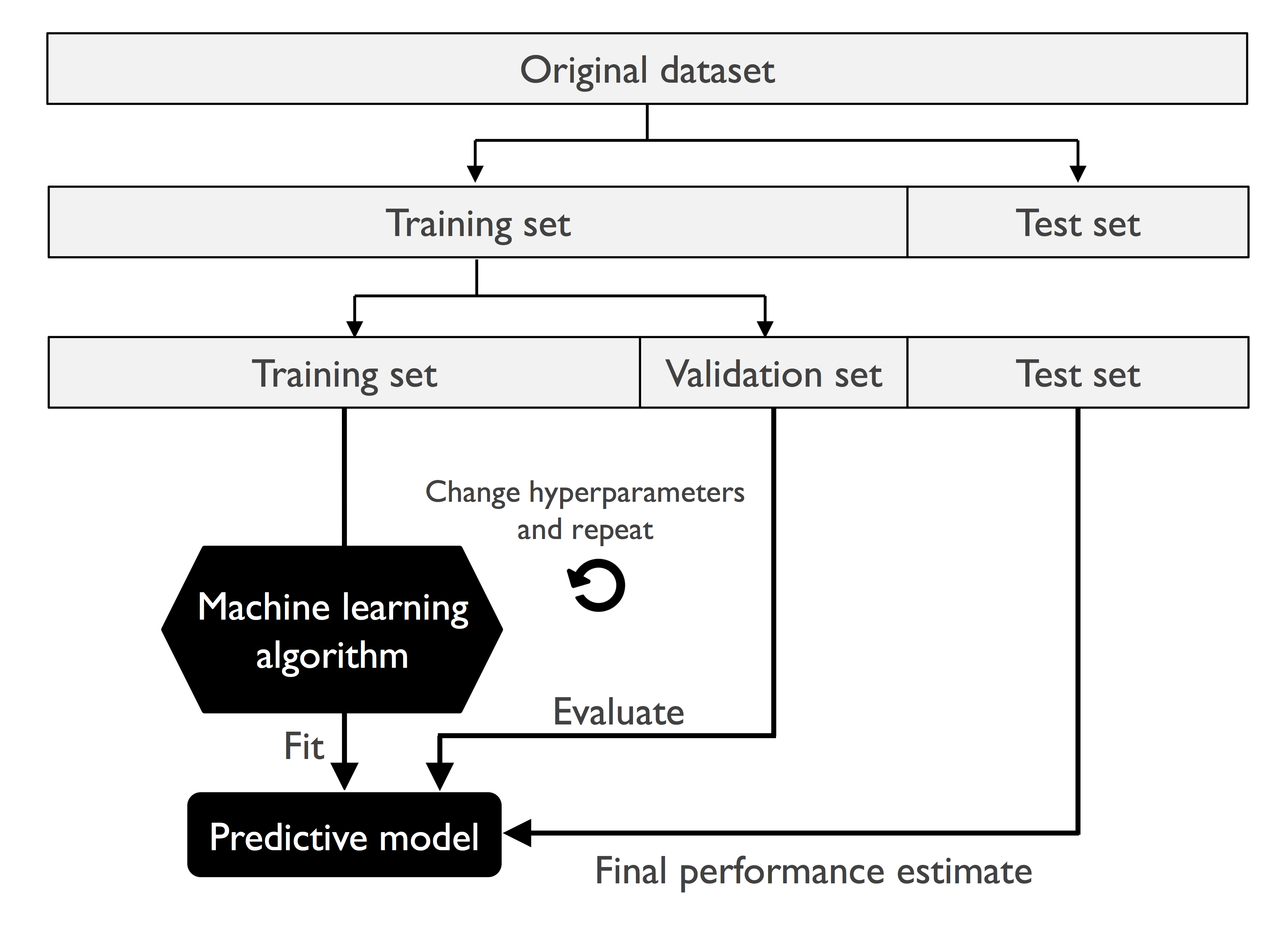
홀드 아웃 단점 : 훈련 데이터를 훈련 데이터셋과 검증 데이터셋으로 나누는 방법에 따라 성능 추정이 민감할 수 있다는 것
so, 좀 더 안정적 성능 추정 기법인 k겹 교차 검증 (훈련 데이터 k부분으로 나누어 k번 홀드아웃 방법 반복)
k-겹 교차 검증
중복 허용하지 않고 훈련 데이터셋을 k개의 폴드fold로 랜덤하게 나눔. k-1개의 폴드로 모델 훈련하고 나머지 하나의 폴드로 성능 평가.
이 과정 k번 반복해 k개의 모델과 성능 추정을 얻음.
서로 다른 독립적 폴드에서 얻은 성능 추정을 기반으로 모델의 평균 성능 계산. 홀드아웃방법에 비해 훈련 데이터셋의 분할에 덜 민감한 성능 추정 얻음 (데이터셋 작을수록 이득)
테스트 데이터셋에서 모델의 성능을 평가할 때 만족할만한 일반화 성능을 내는 최적의 하이파라미터 값 찾기위해 사용
만족스러운 하이퍼파라미터 값 찾은 후 전체 훈련 데이터셋 사용해 모델을 다시 훈련 -> 독립적 테스트 데이터셋 사용해 최종 성능 추정.
k겹 교차검증 후에 전체 훈련 데이터셋으로 모델 학습 이유 : 훈련 샘플 많을수록 학습 알고리즘 더 정확하고 안정적인 모델 만들기 떄문
k겹 교차 검증 장점 : 중복 허용하지 않는 리샘플링 기법이기 때문에 모든 샘플 포인트가 훈련하는 동안 테스트 폴드로 검증에 딱 한번 사용된다.
보통은 k겹 교차 검증 기본값은 10이고 비교적 작은 훈련 데이터셋으로 작업한다면 폴드 개수 늘려야 함. k값 증가하면 더 많은 훈련 데이터가 반복에 사용되고, 모델 성능 평균하여 일반화 성능 추정시 더 낮은 편향 만듦.
대규모 데이터셋으로는 k값 작게해도 모델 평균 성능 정확 추정 가능.
기본 k겹 교차 검증보다 좀 더 향상된 방법 계층적 k겹 교차 검증 있음.
계층적 k겹 교차 검증
각 폴드에서 클래스 비율이 전체 훈련 데이터셋에 있는 클래스 비율을 대표하도록 유지
예제 코드는 밑의 링크 6.2.2 참고
https://github.com/rickiepark/python-machine-learning-book-3rd-edition/blob/master/ch06/ch06.ipynb