[Verilog] Square Matrix Multiplier

• 테스트 환경
  • OS: UBUNTU 22.04 LTS
  • Tool:VIVADO 2023.2

• 설명

  • 행렬곱 일반화 규칙

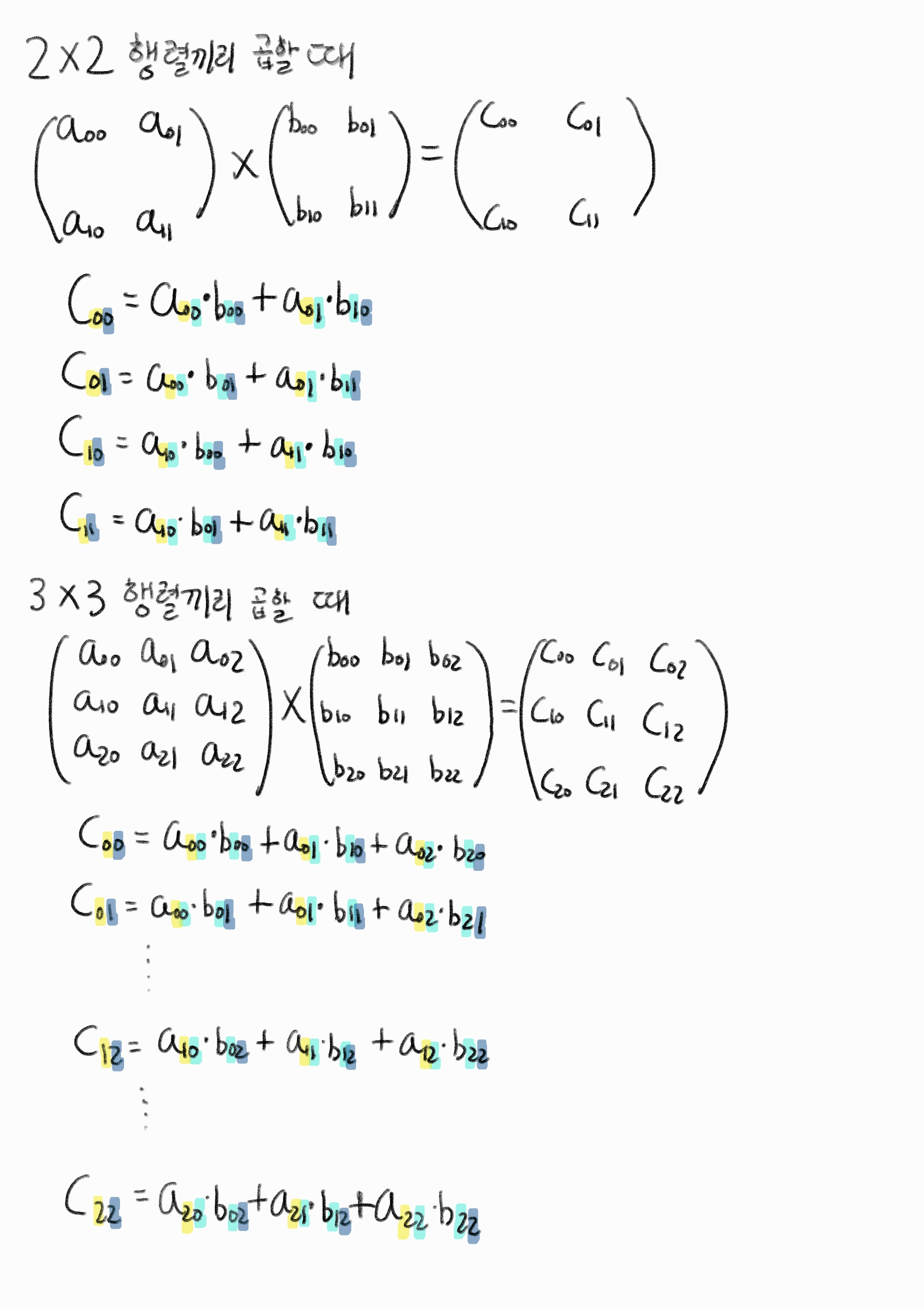
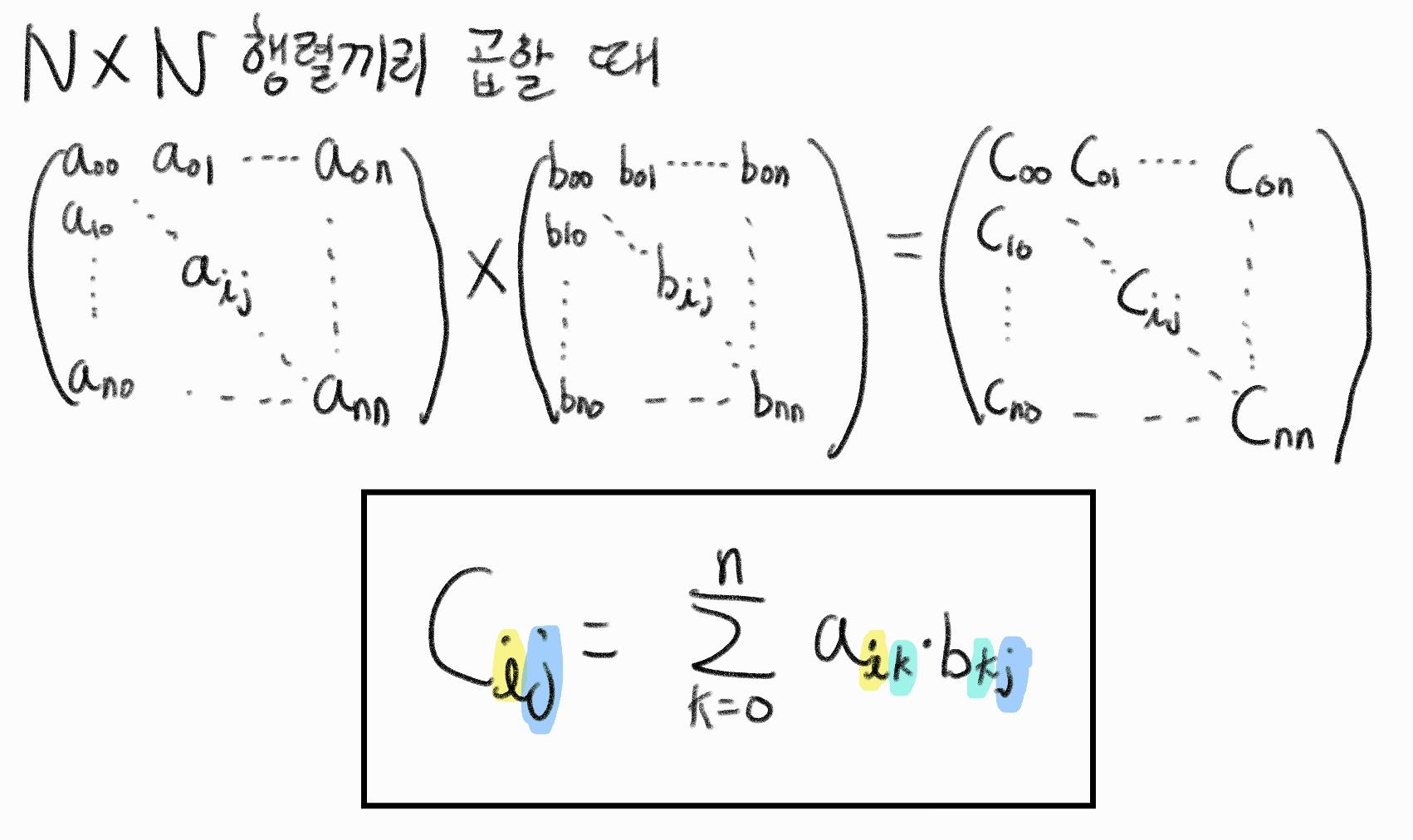
    • 변수 3개로 행렬곱을 일반화 할 수 있다. 즉, 3중 for문으로 모든 요소에 대한 행렬곱 연산을 일반화한 코드를 작성 가능하다.
      
      

  • 배열간 차원 변환

    • Verilog에서 다차원 배열을 input혹은 output으로 설정하는 것은 문법적으로 허용되지 않았다. 아마 HW적으로 입력을 받을 땐 메모리처럼 일차원적으로 입력 및 출력이 가능하기 때문에 이를 반영해서 문법적으로 안되는 것 같아. 찾아보니 systemverilog에선 다차원배열의 입출력이 가능한 것으로 보이는데 이는 Systemverilog의 interface부분만 HW적으로 합성되고 나머지는 SW영역이라서 가능한 것으로 보인다. 따라서 Verilog에서는 입력은 일차원 배열로 받고 내부에서 wire를 배열로 선언하여 연산하도록 설정하였다.
    • 우선 Verilog에서 다차원 배열이 어떻게 표현되는지 살펴보자. 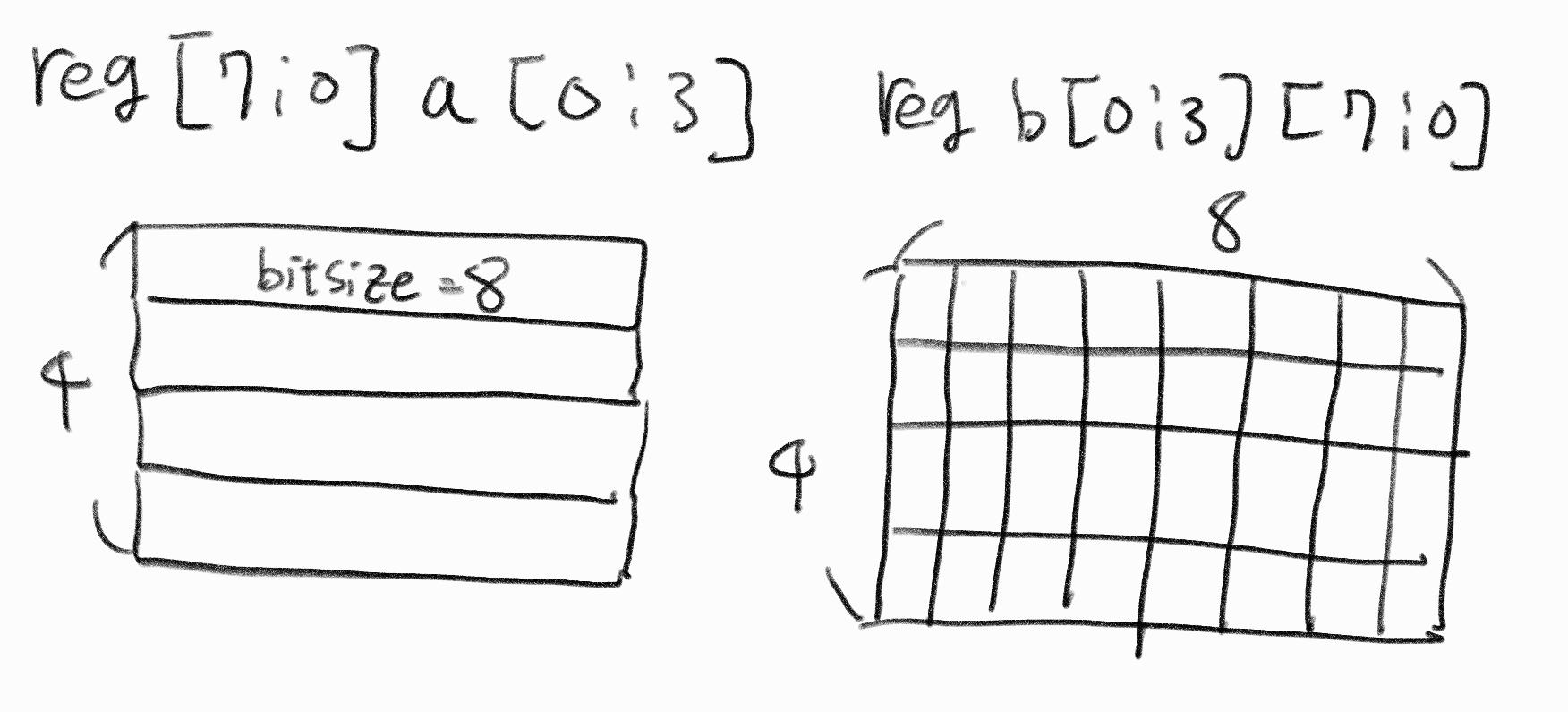이 그림에서 든 예시는 reg타입으로 선언하였다. 왼쪽처럼 선언하면 한 요소의 크기가 8비트만큼의 크기를 갖고 이러한 요소가 4개 있는 배열을 선언한 것이다. 오른쪽처럼 선언하면 한 요소의 크기가 1비트만큼의 크기를 갖고 이러한 요소가 행으로 8개 열로 4개 있는 배열이 선언된 것이다. 실제로 이를 테스트 해보기 위해 VIVADO에서 관련된 코드를 작성해보았다.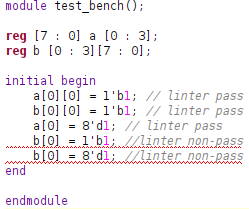위 코드에서 b[0]에 값을 할당하려는 경우 linter에서 밑줄표시가 되는 것을 확인할 수 있다. 즉, 오른쪽처럼 선언한다면 무조건 2차원배열식으로만 접근하며 값을 할당할 수 있는 것이다. 만약 설계한 모듈이 1비트단위로 연산을 수행한다면 우측처럼 선언하여 값이 잘못 할당되거나 초기화되는 문제를 사전에 막는 것도 좋겠지만, 일반적인 설계의 경우 편의성을 위해 좌측처럼 선언하는 것이 좋을 것이라고 생각이 들었다.
      
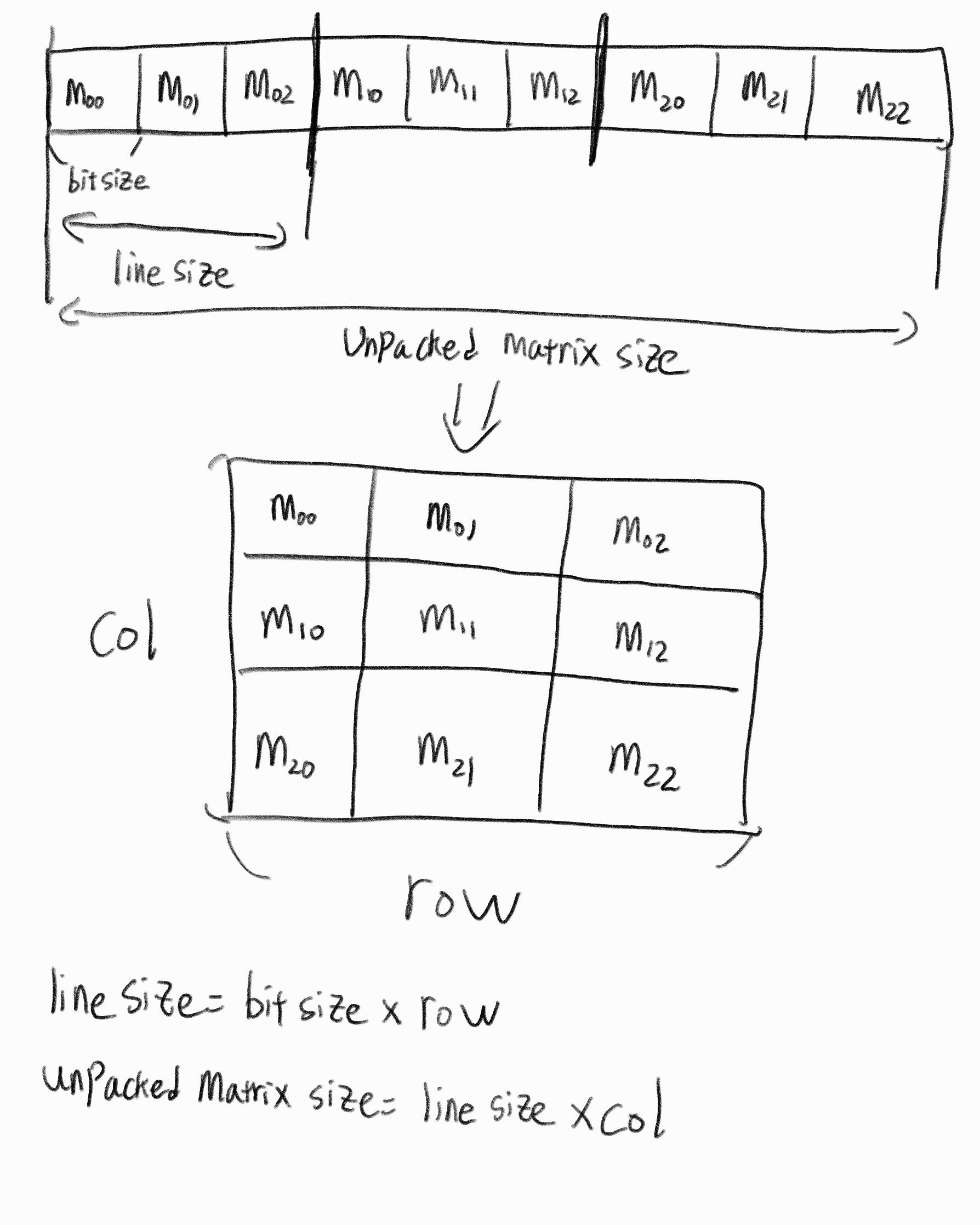
      그렇다면 한 요소의 크기가 1비트가 아닌 2차원 배열은 어떻게 선언할까?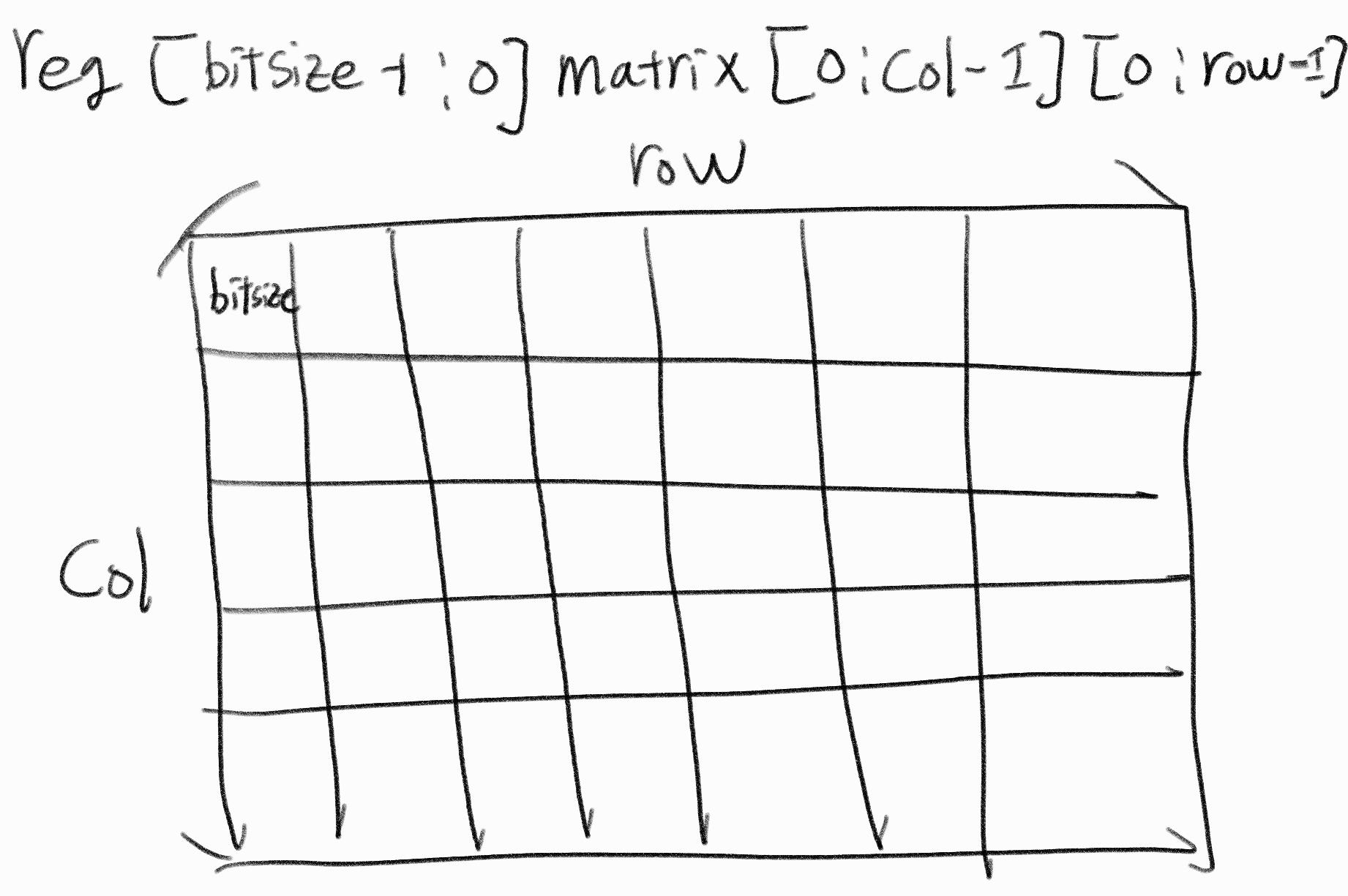 위와 같이 선언하면 한 요소의 크기가 bitsize만큼 갖고, 이러한 요소가 행으로 row개만큼 열로 col만큼 있는 2차원 배열이 선언된다. 이러한 배열을 선언하여 input과 output행렬을 저장하면 될 것이다.
    • 이제 1차원배열을 각 요소의 크기가 bitsize이고, 행과 열의 크기가 row와 col인 배열로 변환하는 방법을 알아보자. 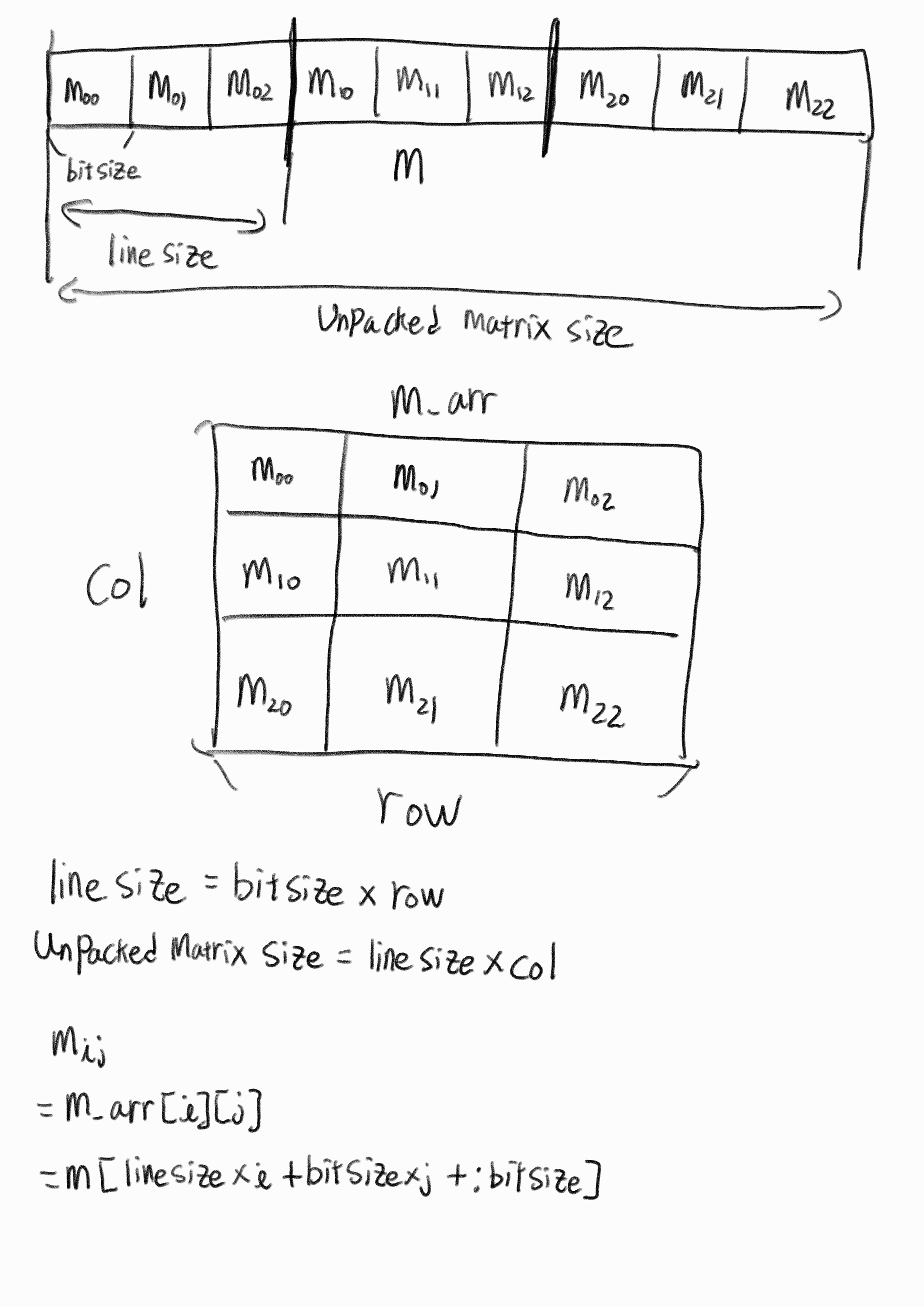한 요소의 크기를 bitsize로 설정하였다. linesize는 열 이동시에 사용하기 위해 설정한 parameter이다. 따라서 linesize는 bitsize와 row의 곱으로 표현된다. unpacked matrix size는 위에서 선언한 한요소의 크기가 bitsize인 2차원 행렬을 1차원행렬로 변환했을 때 사이즈이다. 이는 linesize가 col만큼 있는 크기이다. 이를 활용하면 위 그림에서 나온것과 같이 선언한 행렬과 일차원배열을 대응시킬 수 있다. 여기서 '+:'를 잘 모를 수 있을 것이다. 학부수업에서 다루지 않았던 문법이라서 좀 더 찾아보았다. 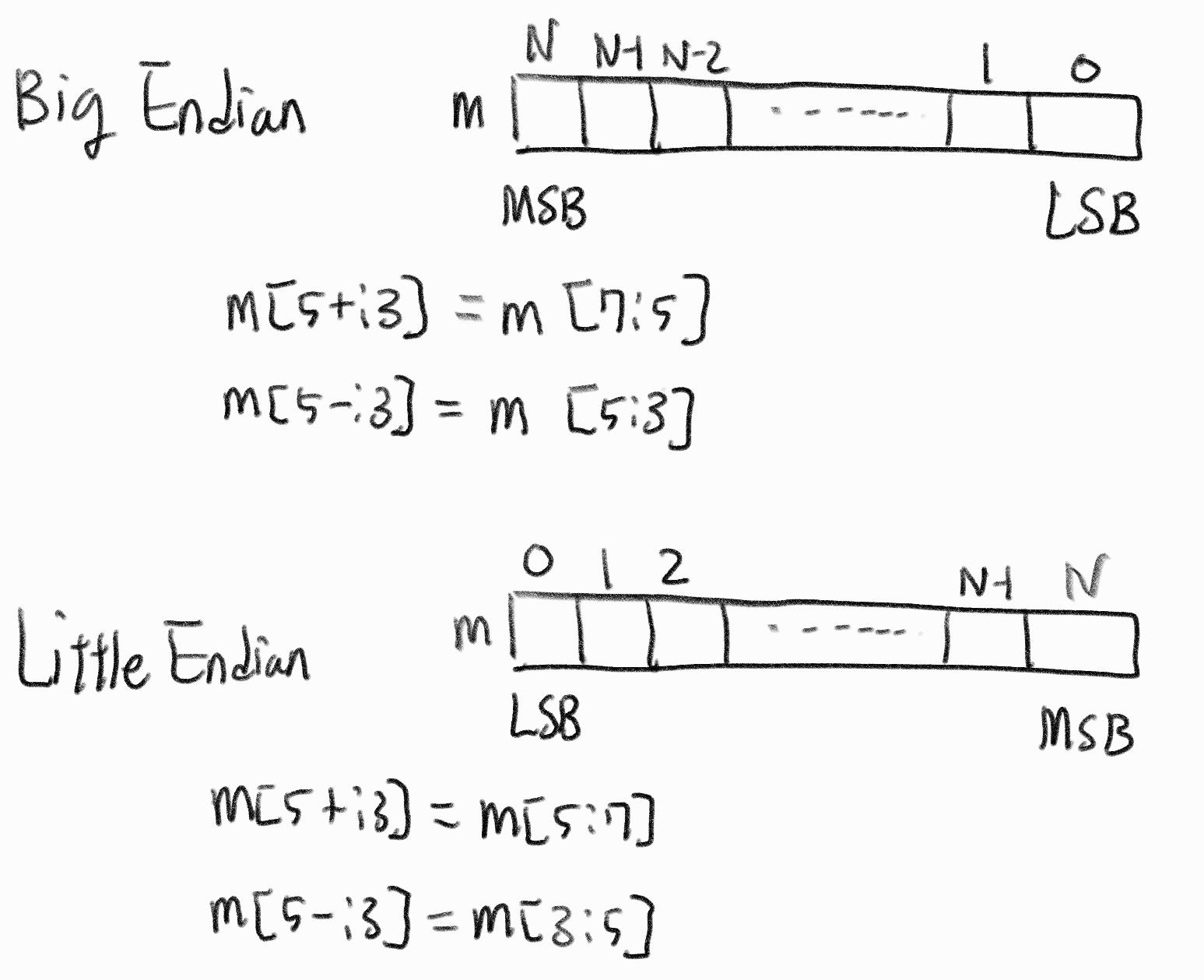정식 명칭은 'indexed part-select'라고 한다. 특징으로는 part select할 대상이 big endian이면 결과물도 big endian으로 나오고, little endian이면 little endian으로 나온다는 것이다. 이를 잘 활용하면 이번에 구현한 모듈처럼 일정한 간격을 갖도록 분할해야하는 상황에서 편하게 구현이 가능할 것으로 보인다. 또한 기존 방식과 다르게 big endian과 little endian을 구분하여 설정할 필요 없이 하나의 방법으로 통일할 수 있다는 장점이 있는 것 같다.
      
      
    • output matrix 크기 설정
      output matrix의 한 요소의 크기는 다음과 같이 설정할 수 있었다. 예를들어 matrix A, B에 있는 요소를 각각 a,b라 하고 각 요소의 bitsize를 2비트라고 한다면 이 두 요소의 곱으로 나올 수 있는 최대 bitsize는 4비트이다. 즉 a's bitsize + b's bitsize = 2 bitsize이다. 하지만 여기서 바로 4bit로 out_m의 한 요소의 bitsize를 설정하면 안된다. 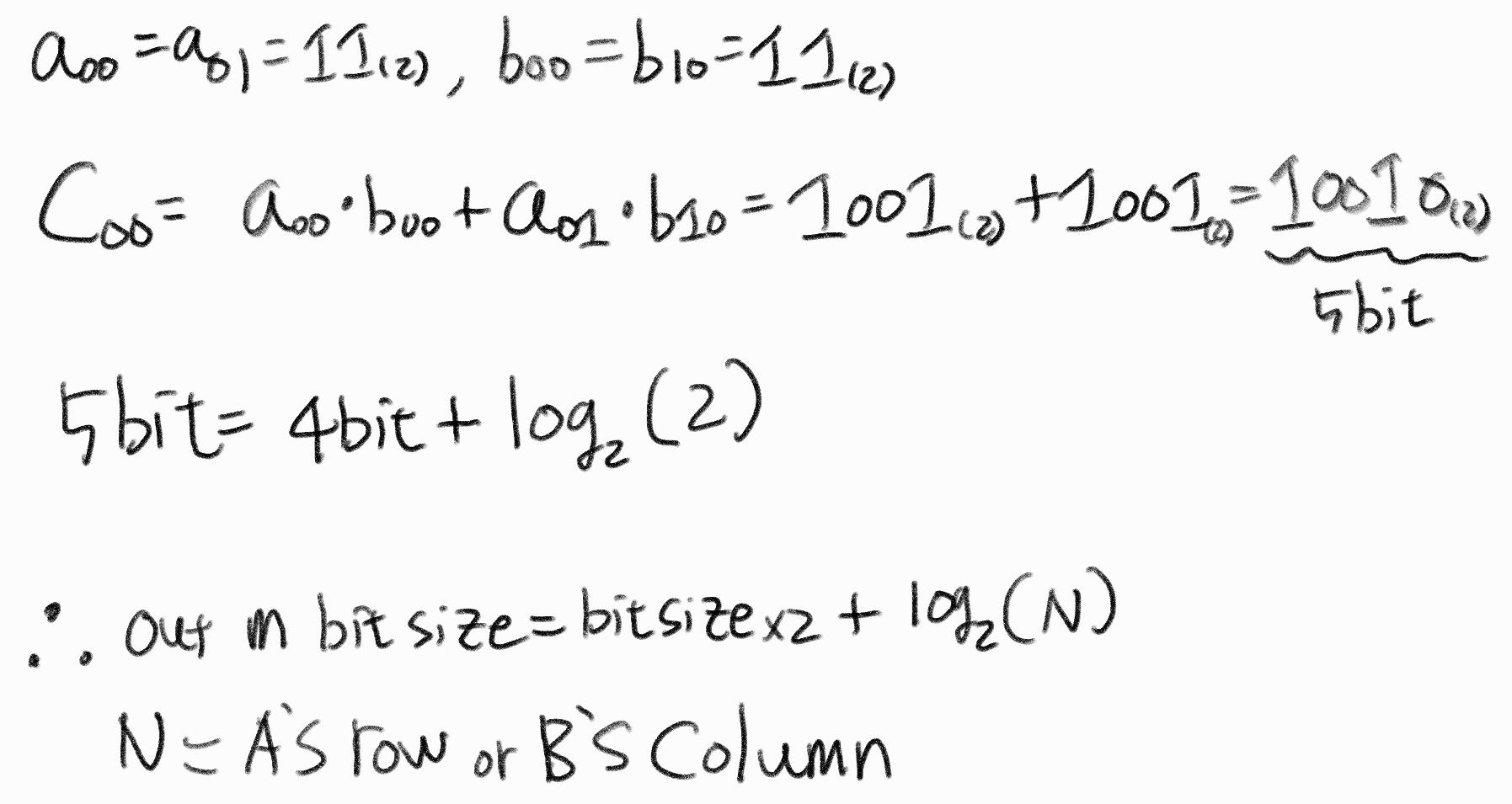즉, 행렬의 크기 또한 결과로 나올 행렬의 요소의 bitsize설정에 영향을 끼친다. 그리고 이를 수식으로 만들면 위의 그림에 나온 수식과 같다.

  • 위에서 설명한 내용들을 반영한 모듈의 소스코드의 링크는 다음과 같다
    Matrix Multiplier Source Code