Zhang, Hongwen, et al. "Pymaf: 3d human pose and shape regression with pyramidal mesh alignment feedback loop." Proceedings of the IEEE/CVF International Conference on Computer Vision. 2021.

1. Introduction

기존의 human mesh 복구작업에 있어 두가지의 방법론이 있었음

1. Optimization-base 방법 : 2d 증거들(features)에서 모델을 fit 하는것
   -> 느림, 초기화 힘듬

   explicitly fit the models to 2D evidences
   
   Bogo, Federica, et al. "Keep it SMPL: Automatic estimation of 3D human pose and shape from a single image." European conference on computer vision. Springer, Cham, 2016.

2. Regression-base 방법 : 이미지로부터 모델 파라미터를 다이렉트하게 뽑아내는 방식
   -> 느림, 믿음직한 결과물, 이미지 feature와 메쉬 사이의 정렬에 대해 고통받음

   suggest to directly predict model parameters from images
   
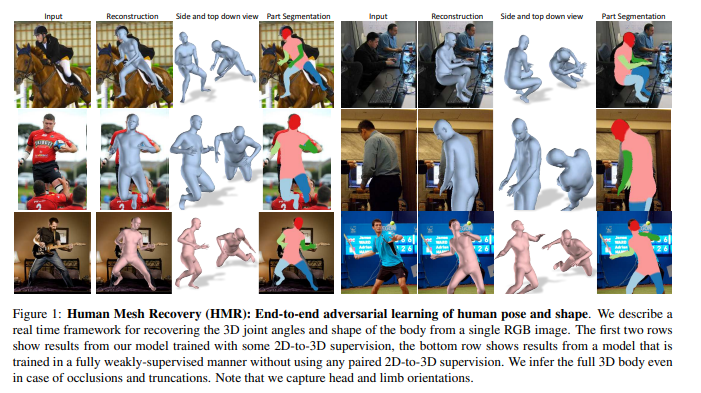
   Kanazawa, Angjoo, et al. "End-to-end recovery of human shape and pose." Proceedings of the IEEE conference on computer vision and pattern recognition. 2018.

SMPL같은 파라미터 모델은 포즈 파라미터를 사용하는데 이때 관절 자세를 부모 관절에 대한 상대적인 회전으로 표현하기 때문에(the kinematic chain) 부모 단 관절의 작은 오류가 자식단에서 눈에띄게 증가할 수 있다.

좋은 결과를 만들기 위해 최적화 기반(Optimization-base) 방법에선 2d 에 투영한 메쉬와 2d feature 사이가 확실하게 최적화 될 수 있는 목적함수를 설계하는 방식을 사용함.

회귀 기반(Regression-base) 방법에서도 이와 비슷한 방법을 사용함
-> 훈련 과정에서 추정된 메쉬의 투영에 2d 지도학습을 적용하기 위해 사용함

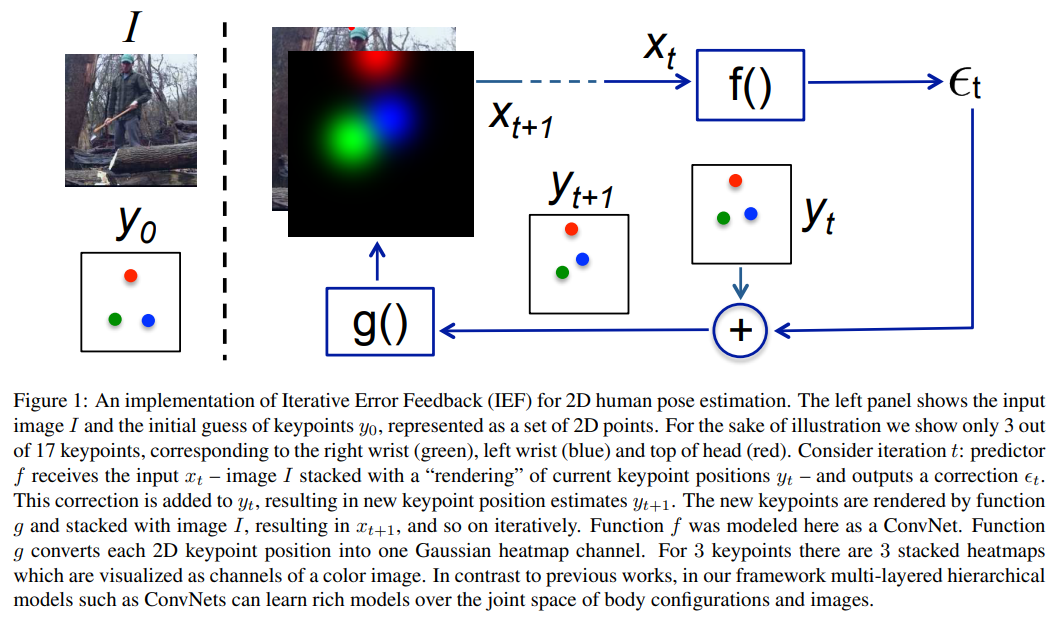
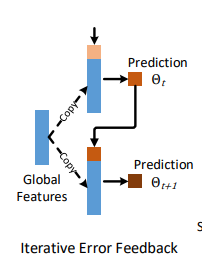
Iterative Error Feedback (IEF)

하지만 test 과정에선 단순하게 아키텍쳐에 IEF(Iterative Error Feedback)이나 open-loop 를 추가함

하지만 IEF는 피드백 루프에서 같은 global feature를 재사용하고 이는 인퍼런스 과정에서 메시와 이미지간의 정렬 오류를 인지하기 힘들게 함.

이전 연구에 따라 신경망은 피쳐 맵의 크기를 줄일 때 높은 수준의 정보를 유지하면서 로컬적인 기능을 폐기하는 경향이 있음.

To leverage spatial information in the regression networks, it is essential to extract pixel-wise contexts for fine-grained perception.

공간적인 정보들을 회귀 네트워크에서 활용하기 위해선 픽셀단위의 정보들을 추출하는게 필수적이다.

dense correspondence : 밀집 정합은 영상에 존재하는 모든 점(Pixel)들
의 대응점을 찾는 과정이다

이러한 픽셀단위 정보들을 사용하기 위해 부분적으로 세그멘테이션 하거나 dense correspondence 방식을 회귀 네트워크에 포함시키는 방식들이 사용되었음.
-> 픽셀단위 정보들을 활용하긴 하지만 구조적인 우선순위와 공간적인 디테일을 오직 하나의 고화질 인풋에서 동시에 학습하는것은 여전히 도전과제임.

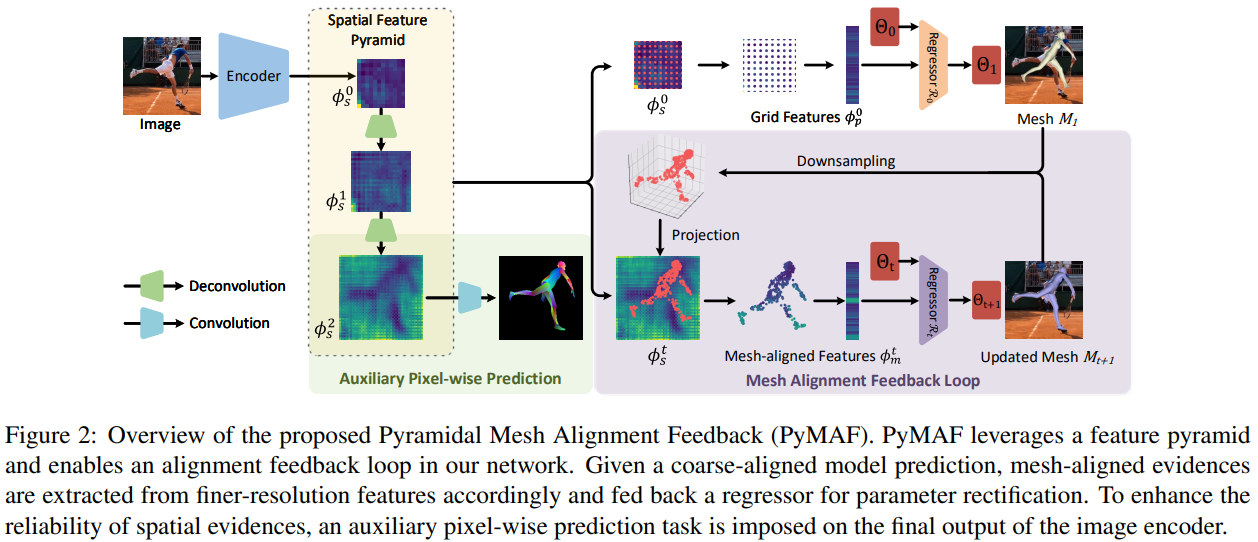
메시와 이미지 사이의 정렬 문제를 해결하기 위해 본 논문에서는 멀티 스케일 정보를 활용하는
Pyramidal Mesh Alignment Feedback (PyMAF) loop 를 디자인하고 회귀 네트워크에 추가하였음.
-> 정렬된 상태를 기반으로 점진적으로 파라메터릭 편차를 고쳐나가는 것.

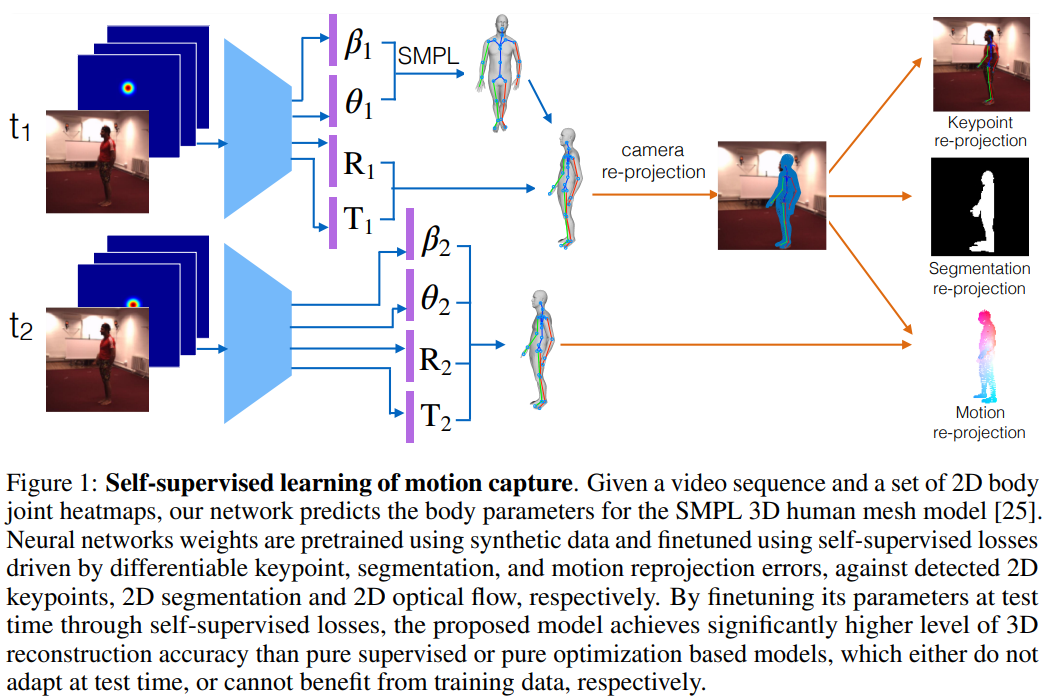
fig 1

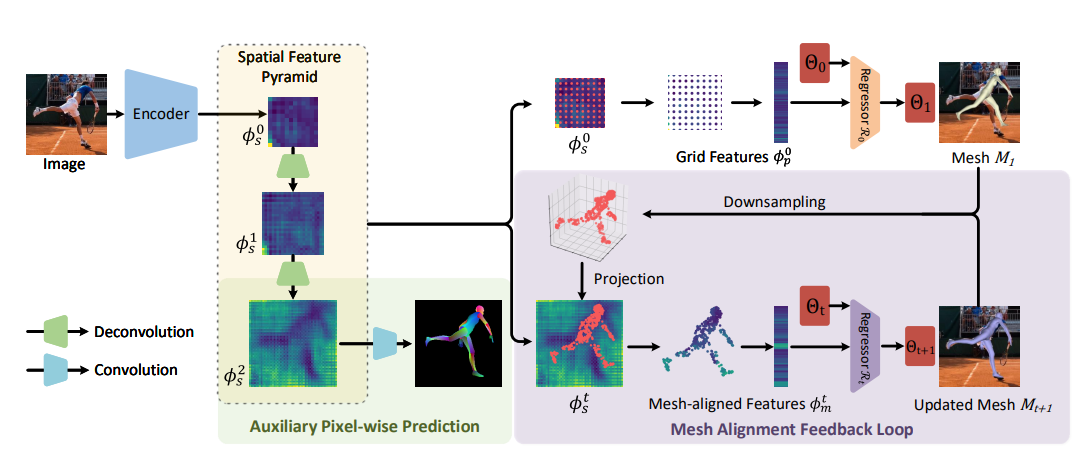
PyMAF 에서 메시와 이미지의 정렬 정보(parameters)는 spatial feature에서 추출되어 다음 매개변수들의 업데이트를 위해 회귀 네트워크에 피드백되어짐.

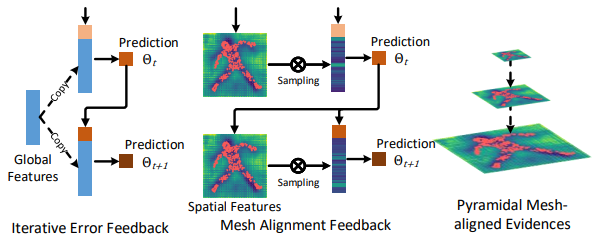
그림 1 에서 보는것처럼 일반적인 IEF 는 첫번째 글로벌 피쳐가 재사용되어 들어가므로 이미지-메시간의 정렬 오류를 찾기가 힘든 반면 mesh alignment feedback 은 예측된 파라미터를 가지고 새로운 mesh를 만들어내고 이를 사용해 다시 매개변수를 업데이트하므로 매개변수 보정에 있어서 더 우월한 성능을 가지고 있음.

To leverage multi-scale contexts, mesh-aligned evidences are extracted from a feature pyramid so that coarse-aligned meshes can be corrected with large step sizes based on the lower-resolution features.

또한 멀티 스케일 정보를 활용하기 위해 메시-이미지 정렬 정보가 피라미드 피쳐에서 추출될 수 있도록 하였음. 그래서 거칠게 정렬된 메시가 낮은 레졸루션의 피쳐부터 높은 레졸루션의 피쳐까지 포함하여 수정 될 수 있도록 함.

main contributions

mesh alignment feedback loop

회귀 기반의 메쉬 모델(SMPL) representation을 위해 사용됨.
메시-이미지의 정렬 증거를 활용하여 추정된 메시가 입력된 이미지와 잘 정렬될 수 있도록
매개변수 오류를 명시적으로 수정함.

feature pyramid

회귀 네트워크가 낮은 레졸루션의 피쳐(높은 수준의 정보만 남은) + 높은 레졸루션의 피쳐(로컬 수준의 정보도 있는) 의 정보들을 활용할 수 있도록 메시 정렬 피드백 루프와 통합시켰음

auxiliary pixel-wise supervision

이미지 인코더를 보조하는 픽셀단위의 지도학습을 적용하여 공간적인 피쳐에서 메시-이미지간의 정렬 정보들이 더 신뢰성이 있어짐.

2. Related Work

2.1. Human Pose and Shape Recovery

Optimization-based Approaches

주로 키포인트나 실루엣같은 2d 관찰에 매개변수 모델(SMPL, SCAPE)을 피팅하는 최적화 프로세스를 사용함.
Optimization-based 오브젝트 함수의 prior terms(loss terms 들)은 부자연스러운 쉐입과 포즈에 패널티를 부여하도록 설계되어있는 반면 데이터 term(데이터로부터 나오는 것들의 loss)은 메시의 재투영한 결과와 2d 이미지의 정보 사이의 적합 오류를 측정함

Regression-based Approaches

Self-supervised Learning of Motion Capture

End-to-end Recovery of Human Shape and Pose

비선형 매핑이 가능한 신경망을 특징을 활용하여 single view 이미지에서 직접 인간 모델을 예측하는 방법이 사용됨.
회귀 네트워크는 2d 증거들을 입력으로 사용함 그리고 모델의 prior를 트레이닝 데이터에 대해 다양한 방식의 지도학습방법을 사용하여 암묵적으로 학습함.
회귀 네트워크의 학습 난이도를 낮추기 위해 실루엣이나, 2d,3d 조인트, 세그멘트, dense correspondences 같은 프록시 표현을 활용하도록 설계되었음
->이러한 방법들은 합성 데이터와 프록시 표현의 이점을 가지고 있음.

이러한 이점에도 불구하고 프록시 표현은 reconstruction task에서 병목현상을 일으킬 수 있음.
이는 회귀 네트워크가 end-to-end 학습을 진행하는것을 방해함.

더욱이 회귀 네트워크가 훈련하면서 발생하는 피팅의 불일치에 패널티를 부여하기 위해 지도학습 신호를 사용하지만 기존의 회귀 네트워크는 인퍼런스 단계에서의 불일치를 거의 파악할 수 없음(왜냐면 입력단이 프록시 데이터이므로 실제 이미지의 정보가 거의 다 사라지기 때문에)

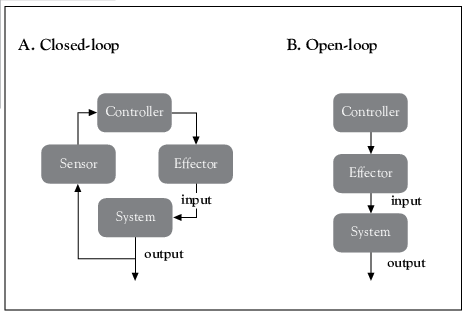
close-loop vs open-loop 차이?..


OPENLOOP: The desired output, AKA the delayed target, is used as an additional input. The OL net will produce output for the common time extent of the input and target.
CLOSELOOP: The delayed target input is replaced by a direct delayed output connection. The CL net will produce output for the time extent of the input.

MATLAB answers

In comparison, the proposed PyMAF is close-loop for both training and inference, which enables a feedback loop in our deep regressor to leverage spatial evidences for better mesh-image alignment of the estimated human models.

반면 PyMAF는 훈련과 인퍼런스에서 모두 사용할 수 있는 닫힌 loop이며(아웃풋을 다시 사용할 수 있으므로) 아웃풋으로 나온 결과를 다시 사용하여 더 나은 메시-이미지 정렬을 할 수 있게 함.

2.2. Iterative Fitting in Regression Tasks

Learning to reconstruct 3D human pose and shape via model-fitting in the loop(SPIN)

회귀 작업에서 피팅 작업을 통합하는 방식도 존재함
훈련 과정에서 반복적인 피팅 작업을 추가하였음
->더 정밀한 GT를 생성하기 위해 훈련 과정에서 반복적으로 피팅함

중간 추정치의 메시를 이미지와 정렬시키기 위해 추정된 메시를 depth map이나 세그멘트, dense correspondence등으로 변형하려는 시도도 있었음
->이러한 접근방식은 피팅하려는 목표를 중간 추정치로 채택하기 때문에 중간 추정치의 퀄리티에 따라서 결과가 달라질 수 있음.

In contrast, our approach uses the currently estimated meshes to extract deep features for refinement, which not only behaves symmetrically for both training and inference but also enables fully end-to-end learning of the deep regressor.

대조적으로 우리 방법은 현재 추정된 메시를 개선을 위한 피쳐를 추출하기 위해 사용함.
->이걸 사용해 end-to-end 학습을 달성하였다고 함

3. Methodology

3.1. Feature Pyramid for Human Mesh Regression

이미지 인코더의 목표는 공간적인 feature들을 뽑아내는 것.(포즈를 취한 사람의 피쳐맵을 다른 스케일의 레벨로 뽑아내기 위해)
-> 거친 피쳐부터 고운 피쳐까지
다른 스케일로 뽑아낸 피쳐맵들(The feature pyramid) 은 SMPL 모델의 파라미터와 카메라 파라미터들($\mathit{\Theta}$)을 뽑아내는데 사용함

$\mathit{\Theta}=\{\theta,\beta,\pi\}$
$\theta$ : SMPL pose parameter
$\beta$ : SMPL shape parameter
$\pi$ : camera parameter

결과적으로 우리는 이미지 I 가 이미지인코더의 인풋으로 들어가면 다음과 같은 spatial features set이 아웃풋으로 나오게 하고 싶음
$\{\phi^t_s\in\mathbb{R}^{C_s\times H^t_s\times W^t_s}\}^{T-1}_{t=0}$
$H^t_s$ 와 $W^t_s$는 t에 따라서 단조롭게 증가함.

$\phi^t_p$ : Grid features
$\phi^t_p=\mathcal{F}(\phi^t_s,X_t)=\oplus(\{f(\phi^t_s(x)),$ for $x$ in $X_t\})$
$\mathcal{F}(\cdot)$ : the feature sampling and processing operations
$t$ : scale level
$\phi^t_s$ : set of spatial features
$X_t$ : sampling points
$x$ : 2d point in $X_t$
$\oplus$ : concatenation
$f(\cdot)$ : MLP

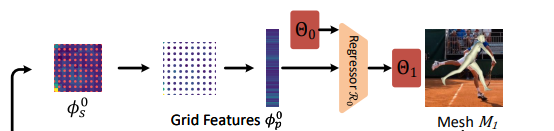
즉 $\phi^t_s$ 는 level t에서의 spatial 피쳐맵이고 $\phi^t_p$는 $\phi^t_s$에서 셈플링한 점 $X_t$ 들을 mlp에 통과시킨다음 컨캣하여 만든 grid feature맵

그다음 파라미터 회귀 네트워크인 $\mathcal{R}$에 가장 최근 측정된 파라미터$\mathit{\Theta}_t$와 $\phi^t_p$ 를 인풋으로 입력하면 아웃풋으로 parameter residual 즉 파라미터의 에러가 출력됨
그리고 $\mathit{\Theta}_t$는 residual을 더하여 $\mathit{\Theta}_{t+1}$으로 업데이트 됨
$\mathit{\Theta}_0$ 은 트레이닝 데이터에서 평균을 구하여 계산

이렇게 파라미터가 각 레벨 t 에 맞게 주워지면 이에 따라서 메시(SMPL)을 생성할 수 있음

SMPL은 3d joint($J\in \mathbb{R}^{N_j\times 3}$)를 회귀할 수 있음 이렇게 회귀한 joint를 2d 에 투영함
$K=\prod(J)\in \mathbb{R}^{N_j\times 2}$
$\prod$ : 카메라 파라미터 $\pi$를 기반으로 한 투영함수

SMPL의 포즈 파라미터 $\theta$는 키네마틱 체인을 사용하는 회전 파라미터임
-> 즉 부모 단에서의 작은 에러가 자식 단에서 커지는 문제를 가지고 있음
이를 해결하기 위해 측정된 SMPL 메시의 관절을 2d에 투영한 다음 2d 지도학습을 하였음
동시에 3d joint, SMPL model parameters 대한 지도학습도 진행하였음

loss function for the parameter regressor

$\mathcal{L}_{reg}=\lambda_{2d}||K-\hat{K}||+\lambda_{3d}||J-\hat{J}||+\lambda_{para}||\mathit{\Theta}-\hat{\mathit{\Theta}}||$
$||\cdot||$ : L2 norm
$\hat{K},\hat{J},\hat{\mathit{\Theta}}$ : 각각 2d joint ,3d joint, SMPL paramter GT (이때 모델 parameter는 pseudo 라벨링 되어있음 SMPLify,HMR 등으로)

보통 회귀 네트워크는 하나의 global feature ($\phi_g$)만 사용하여 공간적인 정보(spatial information)을 잘 활용하지 못했는데 본 논문에서는 level t에 따라 다른 feature ($\phi^t_s$)를 사용함으로써 기존의 방법보다 공간적인 정보를 활용함.

이때 point-wise한 feature를 $\phi^t_s$에서 추출하는 간단한 방법은 $X_t$를 grid 패턴으로 사용하여 균일하게 feature를 셈플링하는것이다.
본문에서 t=0 일때 $X_t$가 grid 패턴을 사용하였고 t>0부터는 측정된 메시로부터 $X_t$를 업데이트시켜서 사용함

3.2. Mesh Alignment Feedback Loop

Iterative Error Feedback

HMR(End-to-end Recovery of Human Shape and Pose) 에서 언급한것처럼 이미지에서 직접 mesh parameter를 회귀하는것은 어려움.
이걸 해결하기 위해 HMR은 Iterative Error Feedback(IEF)라는 방법을 사용하였음
이는 글로벌 피쳐 $\phi_g$ 를 사용해 파라미터 $\mathit{\Theta}$를 업데이트하여 다시 인풋으로 사용하는것임.

문제는 IEF 가 동일한 global featrue $\phi_g$를 사용한다는것임.
-> 글로벌한 피쳐만 사용하므로 로컬의 디테일한 정보를 잃어버림
이와 대조적으로 논문에서 사용한 Mesh Alignment Feedback(MAF) loop는

Mesh Alignment Feedback

회귀 네트워크에서 나온 파라미터를 사용하여 새로운 메시를 추정하고 이에 따른 메시-이미지간의 정렬을 개선할 수 있음.

t>0 일때 현재 추정된 메시 $M_t$ 를 기반으로 $\phi^t_s$에서 메시 정렬 피쳐(Mesh-aligned Feature)를 뽑아 보다 위치에 민감한, 그리고 조금 더 디테일한 로컬 정보를 얻을 수 있게 됨.

즉 글로벌 피쳐 $\phi_g$ 와 메시 정렬 피쳐$\phi^t_m$를 비교하면
메시 정렬 피쳐는 현재 추정된 메시와 이미지의 정렬 상태를 반영할 수 있으므로 $\mathit{\Theta}$ 수정에 있어서 글로벌 피쳐보다 더 적합하다.

이때 어느 점을 셈플링하는지 결정하는것은 $M_t$를 다운셈플링하여($\tilde{M_t}$) 2d 평면에 투영한 점 $X_t=\prod(\tilde{M_t})$을 사용함.

이에 따라 메시정렬 피쳐를 뽑아보면 t>0 일때

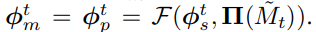
이다.
메시 정렬 피쳐는 현재 파라미터$\mathit{\Theta}_t$ 와 같이 회귀 네트워크의 입력으로 사용되어 업데이트 된 파라미터 $\mathit{\Theta}_{t+1}$를 아웃풋으로 가져오게 됨.

즉 the proposed mesh alignment feedback loop를 다음과 같이 공식화 할 수 있게 됨

$\mathit{\Theta}_{t+1} = \mathit{\Theta}_{t}+\mathcal{R}_t(\mathit{\Theta}_{t},\mathcal{F}(\phi^t_s,\prod(\tilde{M}_t)))$ ,for t>0
(이떄 회귀 네트워크는 residual을 회귀함)

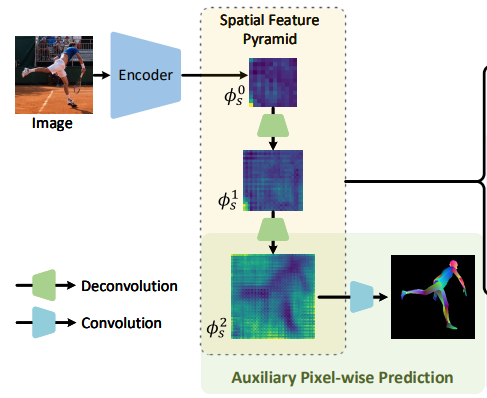
3.3. Auxiliary Pixel-wise Supervision

2번째 줄에서 볼 수 있듯이 입력 이미지의 노이즈가 많은것을 확인 할 수 있음.

이러한 점을 개선하기 위해 마지막 레벨의 spatial feature에 auxiliary pixelwise prediction task를 추가함
-> 마지막 공간 피쳐 $\phi^{T-1}_s$ 는 컨볼루션 레이어를 통과하여 픽셀단위(pixel-wise) dense correspondence maps 을 predict하는 지도학습이 적용되어짐

Dense correspondences 는 2d 이미지 평면의 전경과 3d 공간의 메시 버텍스 사이의 연관 관계를 인코딩하여 매핑하는데 사용함.

이런 방식으로 the auxiliary supervision는 spatial feature map을 만드는 이미지 인코더에 관련성이 높은 정보를 보존하도록 함.

구현할때 DensePose에서 정의한 IUV 맵을 Dense correspondences을 표현할때 사용하였음
IUV맵은 part index와 메시 버텍스의 UV 값으로 구성되어져 있음.

Note that we do not use DensePose annotations in the dataset but render IUV maps based on the ground-truth SMPL models [68].
DensePose의 어노테이션을 사용하지 않았지만 SMPL을 기반으로 IUV 맵을 렌더링함

auxiliary supervision의 loss 함수가 uv 채널과 part index를 패널티하도록 설정됨

part index 채널은 크로스엔트로피를 적용하여 신체부위에 속하는 픽셀을 분류하도록 함

UV 채널의 경우 L1 로스를 사용해 해당 픽셀의 UV값을 회귀하도록 함.

auxiliary supervision object function

$\mathcal{L}_{aux}=\lambda_{pi}CrossEntropy(P,\hat{P})+\lambda_{uv}SmoothL1(\hat{P}\odot U,\hat{P}\odot \hat{U})+\lambda_{uv}SmoothL1(\hat{P}\odot V,\hat{P}\odot \hat{V})$

4. Experiments

4.1. Implementation Details

4.2. Datasets

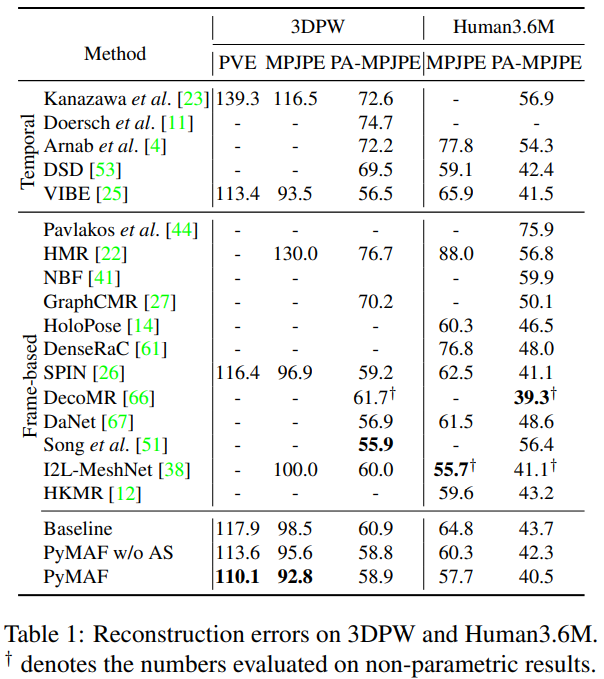
4.3. Comparison with the State of the Art

3D Human Pose and Shape Estimation.