이번 포스트에서는 Decision Tree에 대해서 다룹니다.
Background
어릴 적 스무고개 놀이를 떠올려보면 어떠한 정답에 도달하기 위해 계속 질문을 던져가며 답을 유추해가는 것을 알 수 있다. 단순한 로직이지만 질문을 할수록 정답에 가깝게 유추할 수 있으며 결국엔 정답을 맞히는 것에 성공한다. 이번 포스트에서 다룰 Decision Tree는 스무 고개와 비슷한 알고리즘 형태를 가진다.
Decision Tree
Decision Tree는 단어 뜻 그대로 의사결정 나무라고도 불리며 데이터를 분석하여 패턴을 예측할 수 있는 규칙들의 조합으로 나타내며 Classification과 Regression에도 사용할 수 있는 머신 러닝 기법이다.
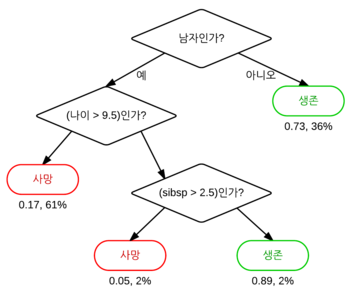
알고리즘의 시작 지점은 Root Node라고 부르며, 중간 지점은 Intermediate Node, 최종 분류 및 회귀 지점을 Terminal Node라고 부른다. 또, 기준 Node의 상위에 있는 Node를 Parent Node라고 하며, 하위에 있는 Node를 Leaf Node 또는 Child Node라고 부른다.
불순도(Impurity)
Decision Tree의 분기 지점은 불순도(Impurity)에 따라 결정된다. 불순도란 해당 범주의 다른 데이터가 얼마나 섞여있는지를 의미한다. 아래의 그림과 같이 같은 범주 안의 다른 데이터들이 섞여있을수록 불순도가 높아지게 되고 모델의 성능이 낮아진다.
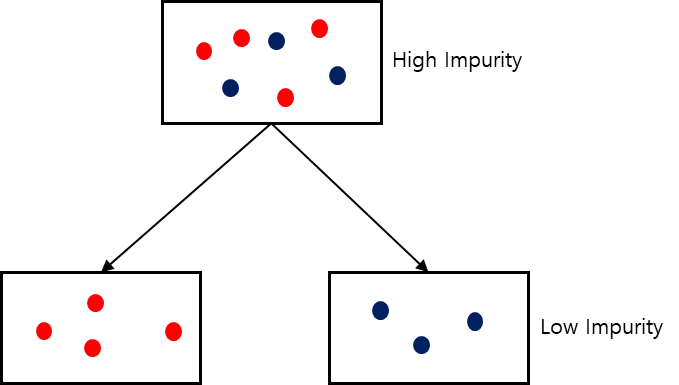
Decision Tree는 현재 Node와 Child Node의 불순도를 차이를 Information Gain이라고 하는데 이를 최소화하는 것을 목표로 한다.
불순도는 대표적으로 두 개의 함수로 수치적으로 표현할 수 있다.
Gini
Gini는 아래의 수식으로 표현되며, n은 범주의 수, p는 데이터가 목표 변수 k번째에 속할 확률이다. 0에 가까울수록(범주의 같은 속성의 데이터만 있을 경우) 불순도가 낮다는 의미이며 0.5가 최대 값이다.
Entropy
Entropy는 아래의 수식으로 표현되며, n은 범주의 수, p는 데이터가 목표 변수 k번째에 속할 확률이다. Gini와 마찬가지로 0에 가까울 수록 불순도가 낮다는 의미이고 Entropy는 1이 최대값이다.
Pruning
모든 최종 지점의 Terminal Node가 순도가 100%인 상태(불순도가 0%)를 Full Tree라고 하는데, 이 Full Tree 상태이거나, Terminal Node가 너무 많은 상태에서는 오버 피팅이 일어 날 가능성이 매우 높다. Terminal Node가 너무 많으면 새로운 데이터에 대한 예측 성능이 매우 떨어질 수 있는데, 트리의 깊이를 제한하거나, Terminal Node를 합쳐주면서 오버 피팅을 어느정도 방지할 수 있다.
Reference
https://en.wikipedia.org/wiki/Decision_tree
https://ko.wikipedia.org/wiki/%EA%B2%B0%EC%A0%95_%ED%8A%B8%EB%A6%AC_%ED%95%99%EC%8A%B5%EB%B2%95 : Image Ref
