이진 힙
힙(heaps)은 트리의 일종이다
트리에 대해 적용되는 것은 일반적으로 힙에도 적용된다
많은 종류의 힙이 있다. 피보나치 힙, 레오나르도 힙, 소프트 힙, 좌측 힙 등
이 중에서 이진 힙을 다룬다
이진 힙은 두 종류가 있다
- Min binary heaps 최소 이진 힙
- Max binary heaps 최대 이진힙
둘은 코드가 비슷하다
heap을 배우는 이유
힙을 이용해서 우선순위 큐라는 것을 만든다
우선순위 큐는 그래프 순회에서 쓰인다
binary heap의 특징
힙은 트리 구조의 일종으로 이진 탐색 트리와 매우 비슷하나 다른 규칙을 가진다
-
최대 이진 힙에서 부모 노드가 항상 자식 노드보다 큰 값을 가진다.
왼쪽 오른쪽 상관없이 한 레벨 아래에 있는 자식 노드보다 항상 부모 노드가 크다
즉 최대 이진 힙에서 모든 자식노드가 부모노드 보다 작다
-
최소 이진 힙에서는 그 반대가 성립한다.
부모노드가 언제나 양쪽의 자식보다 작다 -
이진 탐색 트리와는 다르게 왼쪽과 오른쪽에는 순서가 존재하지 않는다
-
이진 트리처럼 부모 노드는 최대 두개의 자식을 가진다(이진)
-
이진 힙은 언제나 가능한 가장 적은 공간을 차지한다. 즉 한쪽으로 치우친 모양으로 생성되지 않고 다음 밑 레벨로 내려가기 전에 모든 left와 right가 다 채워진다. 한줄에서는 왼쪽이 언제나 먼저 채워진다
-
형제 노드들끼리는 아무 관계가 존재하지 않음. 비교도 X
최대 이진 힙의 인덱스
최대 이진 힙을 루트부터 순서대로 나열한 리스트에서
모든 인덱스 n에 대해 왼쪽 자식은 2n+1에 저장되어 있고 오른쪽 자식은 2n+2에 저장되어 있다
즉, 인덱스의 숫자에 2를 곱하고 1을 더하면 왼쪽이 나오고, 2를 더하면 오른쪽이 나온다.
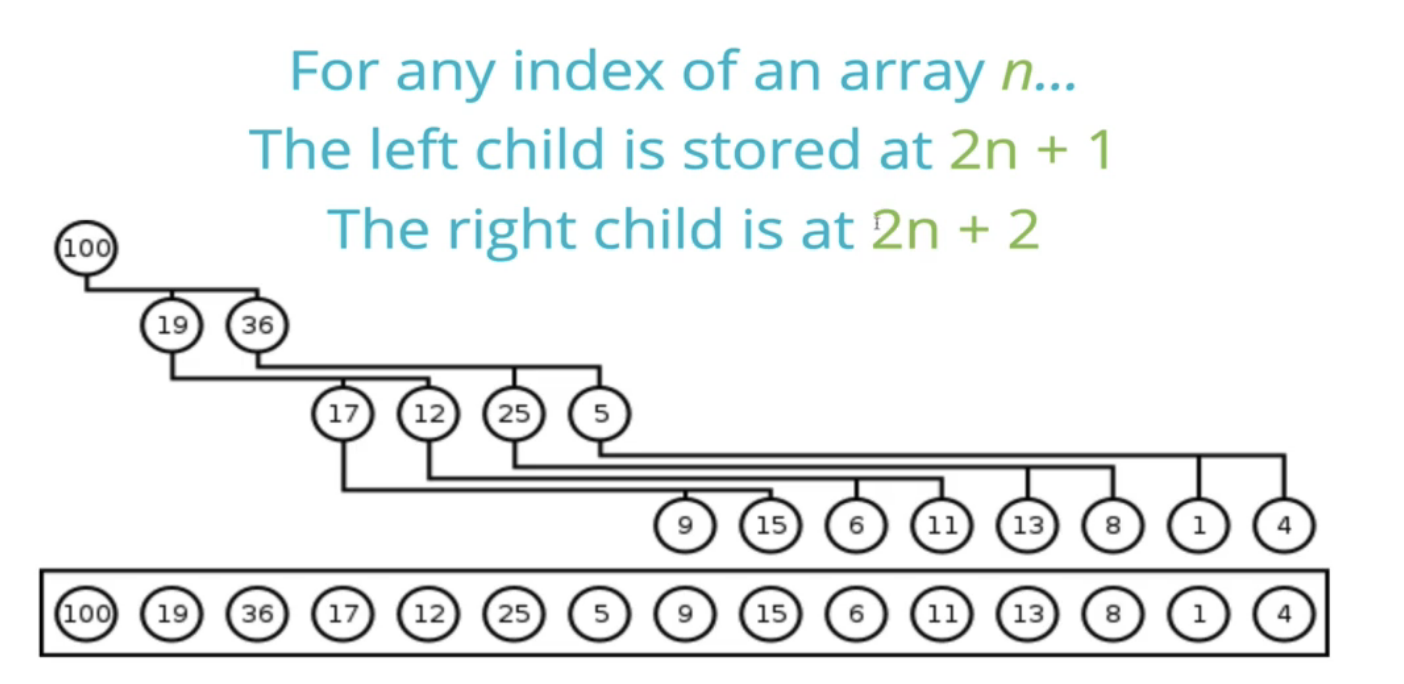
반대로 자식 노드의 인덱스를 가지고 부모 노드의 인덱스를 알수도 있다.
자식 인덱스 n → 1을 빼고 2로 나눈 다음 내림을 한다. 그럼 부모 인덱스다.
Binary heap 구현
트리를 구현할때처럼 노드를 만들어서 하나씩 연결하는 대신에
그냥 배열에 저장해서 그 위치를 기반으로 구조를 모형화한다
즉 위치 값, 인덱스에 상응하는 개별 숫자들이 힙의 구조를 보여주게 된다.
이진 힙 시각화 자료 (visualgo)
https://visualgo.net/en/heap?slide=1
최대 이진 힙에 값을 추가하는 것은 이진 트리보다는 조금 복잡하다
배열의 맨 마지막에 push한 다음 제자리를 찾아준다(bubble up)
최대 이진 힙에 값을 추가하기
- Add to the end
- Bubble up : 부모 노드와 비교해서 더 크면 둘의 자리를 바꾸어 준다
class MaxBinaryHeap {
constructor(){
this.values = []; // 이진힙은 트리 노드가 없고 오직 값을 저장하는 배열, 리스트만 있다. 위치기반 구조를 모형화
}
insert(element){
this.values.push(element); // 맨 뒤에 새로 추가할 엘리먼트를 넣고
this.bubbleUp(); // 버블 업
}
bubbleUp(){
let idx = this.values.length - 1; // 맨뒤에 넣었으므로 인덱스는 길이-1
const element = this.values[idx]; // 새로 넣은 엘리먼트
while(idx > 0){ // 인덱스가 루트가 아니면 계속 반복. 밑에 break가 있다
let parentIdx = Math.floor((idx - 1)/2); // 위 이진 힙의 인덱스 공식대로
let parent = this.values[parentIdx]; // 부모 인덱스의 값
if(element <= parent) break; // 부모 인덱스의 값과 비교해서 부모가 더 크면 break
this.values[parentIdx] = element; // 아니면 자리 바꿈.
this.values[idx] = parent; // 자리를 바꾼다.
idx = parentIdx; // 인덱스도 원래 부모 인덱스로 바꾼다.
}
}
}힙에서 제거하기
Extract me
가장 큰 값인 루트를 제거하면, 배열의 마지막 엘리먼트가 루트 자리로 간다.
그 다음 자식 노드들과 비교해서 자리를 바꾼다. 자식 노드 2개중 큰 값과.
insert에서의 bubble up과 반대되는 sink down.
class MaxBinaryHeap {
constructor(){
this.values = [];
}
extractMax() {
const max = this.values[0]; // 맨 앞에 있는 값. 즉 root
const end = this.values.pop(); // 맨 뒤에 있는 값을 없애면서 end에 넣음
if(this.values.length > 0) {
this.values[0] = end; // 맨 앞에 있는 값을 위에 end로 바꿈
this.sinkDown(); // 밑에 선언하는 sinkDown 호이스팅
}
return max; // 원래 맨 앞에 있던 max를 리턴
}
sinkDown() {
let idx = 0;
const length = this.values.length; // 배열의 길이
const element = this.values[0]; // 현재 인덱스 값.
while(true) { // break를 만나기 전까지 계속 반복
let leftChildIdx = 2 * idx + 1; // 현재 인덱스의 왼쪽 자식 인덱스
let rightChildIdx = 2 * idx + 2; // 오른쪽 자식 인덱스
let leftChild, rightChild;
let swap = null;
if(leftChildIdx < length) { // 왼쪽 자식이 있으면
leftChild = this.values[leftChildIdx]; // 왼쪽 자식의 값을 할당하고
if(leftChild > element) { // 현재 인덱스 값과 비교한 후 더 크면
swap = leftChildIdx; // 스왑은 왼쪽 자식의 인덱스가 된다
}
}
if(rightChildIdx < length) { // 오른쪽 자식이 있으면
rightChild = this.values[rightChildIdx]; // 오른쪽 자식 값 할당하고
if(
(swap === null && rightChild > element) || // 왼쪽 자식이 현재 인덱스값보다 작고 오른쪽 자식이 현재값보다 큰 경우
(swap !== null && rightChild > leftChild) // 왼쪽 자식이 현재 인덱스 값보다 크지만 오른쪽 자식이 왼쪽 자식보다 큰 경우
) {
swap = rightChildIdx; // 스왑은 오른쪽 자식의 인덱스가 된다.
}
}
if(swap === null) break; // 스왑이 null이라면, 즉 왼쪽 오른쪽 둘다 현재 인덱스 보다 작다면 break.
this.values[idx] = this.values[swap]; //현재 인덱스 값을 swap할 자식 값으로 바꾼다.
this.values[swap] = element; //swap한 자식의 값은 현재 인덱스 값으로 바꾼다.
idx = swap; // 현재 인덱스는 스왑한 자식의 인덱스 위치로 바꾼다.
}
}
}Priority Queue 우선순위 큐
우선순위 큐는 각 요소가 그에 해당하는 우선순위를 가지는 데이터 구조이다
더 높은 우선순위를 가진 요소가 더 낮은 우선순위를 가진 요소보다 먼저 처리된다
응급실의 대기줄 같은 것이다. 모든 사람의 중요도가 다르다. 더 급한 환자가 있다
총에 맞은 사람이 오면, 그 앞에 100명의 감기환자가 기다리고 있더라도 총 맞은 사람이 가장 먼저 진료를 받는다.
서로 다른 우선순위를 가지는 데이터를 관리하거나
무언가 입력하는데 입력하는 것이 순서대로 낮은 우선순위를 가지지 않거나
Naive version
순진한 접근에서는 큐를 이루는 요소들의 중요도 priority를 매번 처음부터 끝까지 순회하며 가장 중요한 것을 골라야 한다. O(n)
이진 힙을 이용하면 새로운 요소가 들어올때 루트로 올리고 sinkdown하면서 처리할 수 있다. O(log n)
이진 힙을 이용한 우선순위 큐
class Node {
constructor(val, priority){ // 우선순위 큐의 각 노드는 값val, 우선순위priority를 가진다
this.val = val;
this.priority = priority; // priority는 숫자가 낮을수록 중요함.
}
}
class PriorityQueue {
constructor(){
this.values = []; // 이진 힙 배열
}
enqueue(val, priority){ // 큐에 추가
let newNode = new Node(val, priority); //새로운 노드를 만들고
this.values.push(newNode); // 배열 뒤에 push
this.bubbleUp(); //이진에서 했던 부모노드와 비교해서 자리 바꾸기
}
bubbleUp(){
let idx = this.values.length - 1; // idx는 맨뒤 인덱스로
const element = this.values[idx]; // 새로 추가한 맨 뒤값
while(idx > 0){
let parentIdx = Math.floor((idx - 1)/2); // 부모 노드의 인덱스구하기
let parent = this.values[parentIdx]; // 부모 노드의 값
if(element.priority >= parent.priority) break; //부모 노드의 중요도와 새로 추가한 노드의 중요도를 비교해서 부모노드가 더 중요(숫자가 작은)면 break;
this.values[parentIdx] = element; // 새로 추가한 노드가 더 중요하면 자리바꿈
this.values[idx] = parent; // 자리 바꿈
idx = parentIdx; // 자리바꾸면 인덱스도 바꿈
}
}
dequeue(){ // 큐에서 빼기
const min = this.values[0]; // 이진힙 배열의 맨 앞에 값
const end = this.values.pop(); // 배열의 마지막 값을 빼고 end로 할당
if(this.values.length > 0){ // 배열이 비어있지 않으면
this.values[0] = end; // 맨 앞의 노드를 위에서 할당한 마지막 노드로 바꾸고
this.sinkDown(); // sinkDown.
}
return min; //맨 앞에 값을 리턴.
}
sinkDown(){ // sinkDown 가라앉는다는 뜻이지만 기능은 결국 가장 중요한 노드를 맨 앞으로 보낸다.
let idx = 0;
const length = this.values.length;
const element = this.values[0]; //맨 앞의 노드. 즉 dequeue에서 마지막에 있던 노드다.
while(true){
let leftChildIdx = 2 * idx + 1; //루트의 왼쪽 자식 인덱스
let rightChildIdx = 2 * idx + 2; //오른쪽 자식 인덱스
let leftChild,rightChild;
let swap = null; // swap은 null로 선언하고
if(leftChildIdx < length){ //왼쪽 자식이 존재하면
leftChild = this.values[leftChildIdx]; //왼쪽 자식 노드를
if(leftChild.priority < element.priority) { //현재 노보다 중요하면(priority숫자가 작으면)
swap = leftChildIdx; // 스왑한다.
}
}
if(rightChildIdx < length){ // 오른쪽 자식이 존재하면
rightChild = this.values[rightChildIdx];
if(
(swap === null && rightChild.priority < element.priority) || //1. 왼쪽노드는 현재노드보다 덜 중요하고 오른쪽 노드가 현재노드보다 중요
(swap !== null && rightChild.priority < leftChild.priority) //2. 왼쪽노드가 현재노드보다 중요한데 오른쪽 노드가 왼쪽노드보다 중요
) {
swap = rightChildIdx; // 스왑을 오른쪽 노드 인덱스로 바꿈
}
}
if(swap === null) break; //스왑이 null이면 (위 if문 두개다 작동안했다면, 즉 현재 노드가 자식 노드 두개보다 더 중요하면)
this.values[idx] = this.values[swap]; //현재 노드를 swap할 자식노드와 바꿈
this.values[swap] = element; //바꾼 자식 노드를 바꿈
idx = swap; // 그리고 현재 노드의 인덱스도 바꾼 자식 노드의 인덱스로 바꿈
}
}
}Binary heap의 Big-O
시간 복잡도
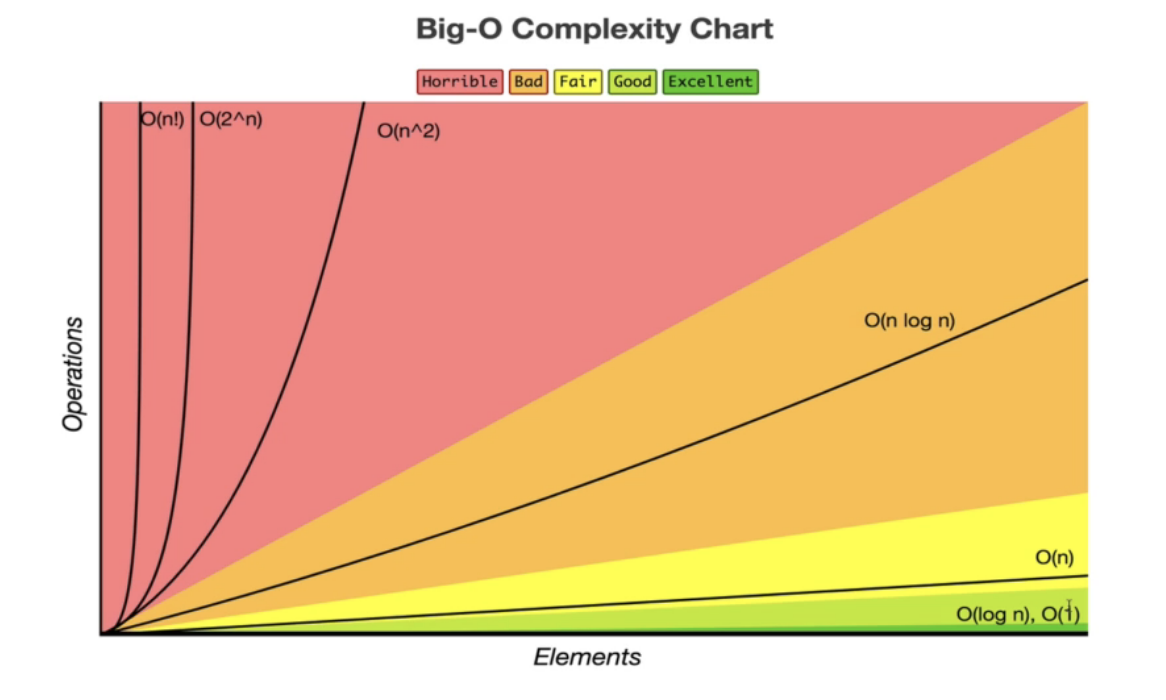
insertion - O(log n)
removal - O(log n)
search - O(n)
이진 힙은 최대 힙이든 최소 힙이든 삽입과 삭제 모두 성능이 좋다
이진힙은 삽입과 삭제에서 O(log n)의 시간복잡도를 가진다
비교해야 하는 데이터 배열이 2배의 길이가 되어도, 이진 힙에서는 한번의 과정만 추가하면 된다.
따라서 log 2 n이 되는 것.
16개 요소 → 4번 비교
32개 요소 → 5번 비교
이진 힙 트리에서 노드의 개수가 2배가 되어도, 층이 하나 더 생기는 것이다.
거기에 이진 힙에서는 트리에서의 이상한 모양( right만 계속 존재하는 형태)가 있을 수 없기 때문에 최악의 경우에도 log n이다.
하지만 이진 힙은 탑색을 위한 것이 아니다.
탐색에 최적화되기를 원한다면 이진 탐색 트리를 쓰는 것이 낫다.
이진 힙은 탐색에 대해서는 O(n)이다.
왜냐면 형제 노드 사이에 주어진 순서가 없으니까.
어디에 찾는 값이 있는지 알수없다. 전부 다 순회해야 한다
부모노드가 찾는 값보다 작으면 그 노드 밑으로 제거하는 식으로 해도 O(n/2)정도인데 어차피 O(n)이다.
즉 이진 힙은 삽입과 삭제에서 유리하고 탐색에는 불리하다. 따라서 우선순위 큐에 사용한다.
