1. 다항함수
#1. 다항함수1
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 2, 100) #-3부터 2까지의 범위에서 균일한 가격으로 100개의 숫자 생성
y = 3 * x**2 + 2
#출력
#array([-3. , -2.94949495, -2.8989899 , -2.84848485, -2.7979798 #,
# -2.74747475, -2.6969697 , -2.64646465, -2.5959596 , #-2.54545455,
# -2.49494949, -2.44444444, -2.39393939, -2.34343434, #-2.29292929,
# -2.24242424, -2.19191919, -2.14141414, -2.09090909, #-2.04040404,
# -1.98989899, -1.93939394, -1.88888889, -1.83838384, -1.78787879,
....
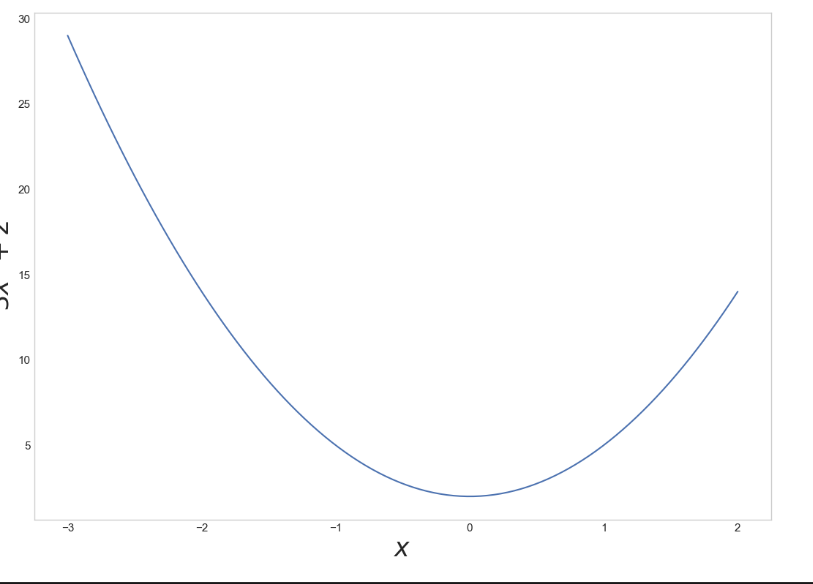
2. 시각화
import matplotlib as mpl
mpl.style.use('seaborn-whitegrid')
plt.figure(figsize=(13,9))
plt.plot(x,y)
plt.grid()
#수학 기호 넣어보기
# plt.xlabel('$x$')
plt.xlabel('$x$', fontsize=25)
plt.ylabel('$3x^2 +2$', fontsize=25)
plt.show()
3. 다항함수2
x = np.linspace(-3, 2, 100)
y1 = 3 * x**2 + 2
y2 = 3 * (x+1) **2 + 2
4.시각화
import matplotlib as mpl
plt.figure(figsize=(13,9))
plt.plot(x,y1, lw=2, ls='dashed', label='$y=3x^2 + 2$')
plt.plot(x, y2, label = '$y=3(x+1)^2 + 2$')
plt.legend(fontsize=15)
plt.grid()
plt.xlabel('$x$', fontsize=25)
plt.ylabel('$y$', fontsize=25)
plt.show()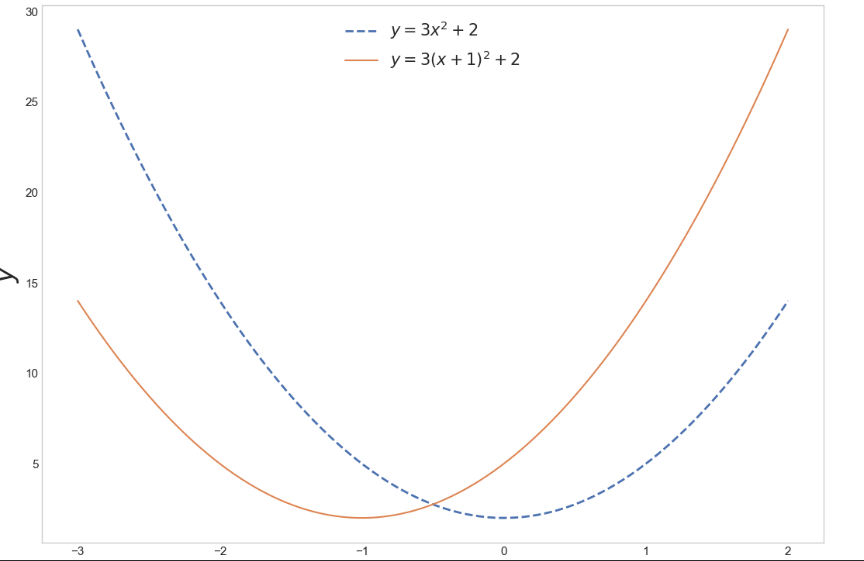
2. 지수함수
1. 지수함수1
a11, a12, a13 = 2,3,4
y11, y12, y13 = a11**x, a12**x, a13**x
a21, a22, a23 = 1/2, 1/3, 1/4
y21, y22, y23 = a21**x, a22**x, a23**x
2.
fig, ax = plt.subplots(1, 2, figsize=(12,6))
ax[0].plot(x, y11, color = 'k', label='$2^x$')
ax[0].plot(x, y12, '--', color='k', label='$3^x$')
ax[0].plot(x, y13, ':', color = 'k', label = '$4^x$')
ax[0].legend(fontsize=20)
ax[1].plot(x, y21, color = 'k', label='$(1/2)^x$')
ax[1].plot(x, y22, '--', color='k', label='$(1/3)^x$')
ax[1].plot(x, y23, ':', color = 'k', label = '$(1/4)^x$')
ax[1].legend(fontsize=20)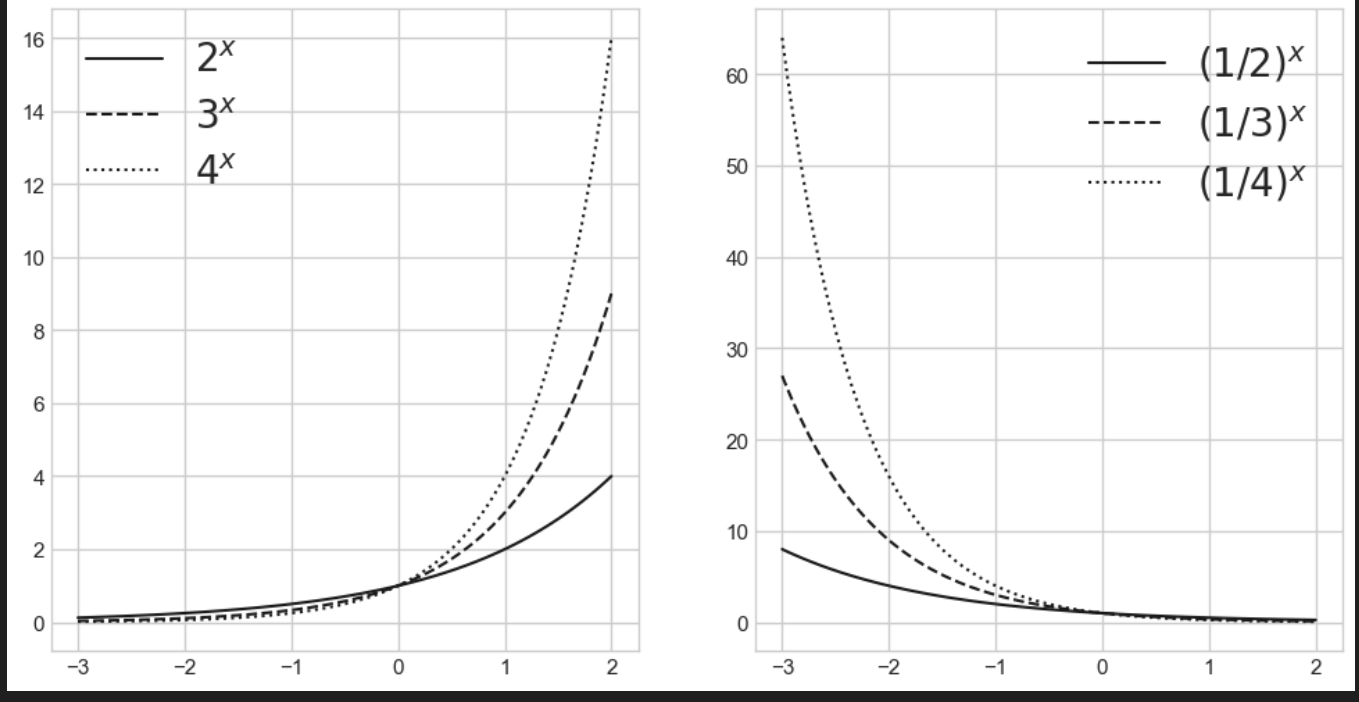
3. 지수함수2
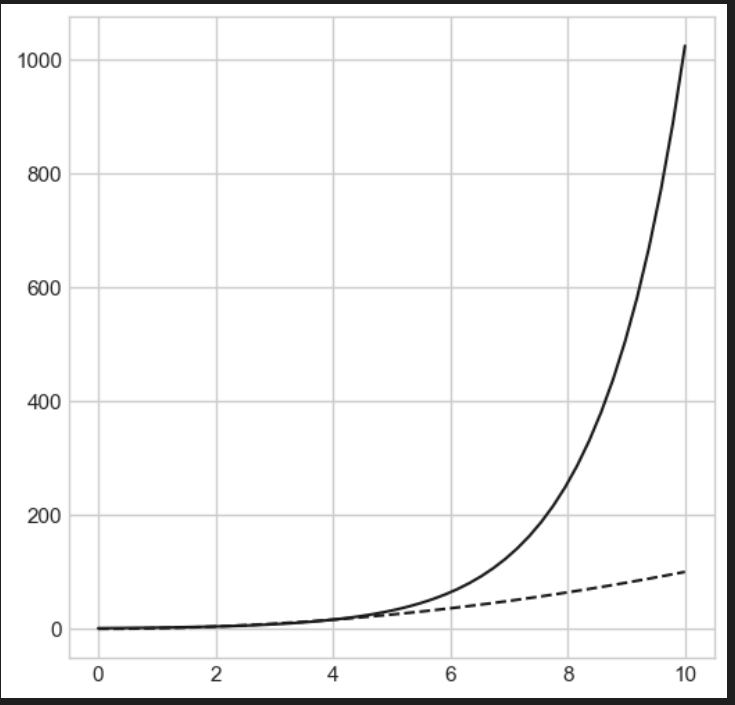
3. 지수 함수 극한 확인
1.
# 지수함수 극한 확인
x = np.array([10, 100, 1000, 10000, 100000, 1000000,10000000])
(1 + 1/x)**x
#출력 결과 어떤 큰 값을 넣어도2.718281828459045에 수렴한다.
# x값이 뭏한히 커질수록 자연상수(e)에 근접하게 된다.
#출력
array([2.59374246, 2.70481383, 2.71692393, 2.71814593, 2.71826824,
2.71828047, 2.71828169])
2. 로그 그리기
np.log(np.exp(1))
# 출력 1.0
3. 자연상수(e)를 나타내는 값
np.e, np.exp(1)
#출력 (2.718281828459045, 2.718281828459045)
4. 그래프
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
ax[0].plot(x1, y11, label='$\log_{10} x$', color='k') # 로그 밑이 10인 로그함수 그래프를 그린다.
ax[0].plot(x2, y12, '--', label='$\log_{e} x$', color='k') # 자연로그 그래프를 점선으로 그린다.
ax[0].set_xlabel('$x$', fontsize=25)
ax[0].set_ylabel('$y$', fontsize=25)
ax[0].legend(fontsize=20, loc='lower right')
ax[1].plot(x1, y21, label='$\log_{1/10} x$', color='k') # 로그 밑이 1/10인 로그함수 그래프를 그린다.
ax[1].plot(x2, y22, '--', label='$\log_{1/e} x$', color='k') # 자연로그 그래프를 점선으로 그린다.
ax[1].set_xlabel('$x$', fontsize=25)
ax[1].set_ylabel('$y$', fontsize=25)
ax[1].legend(fontsize=20, loc='upper right')
plt.show()
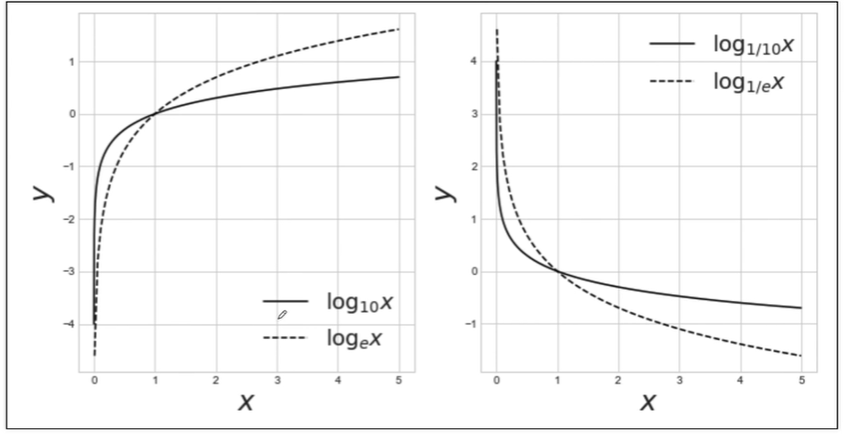
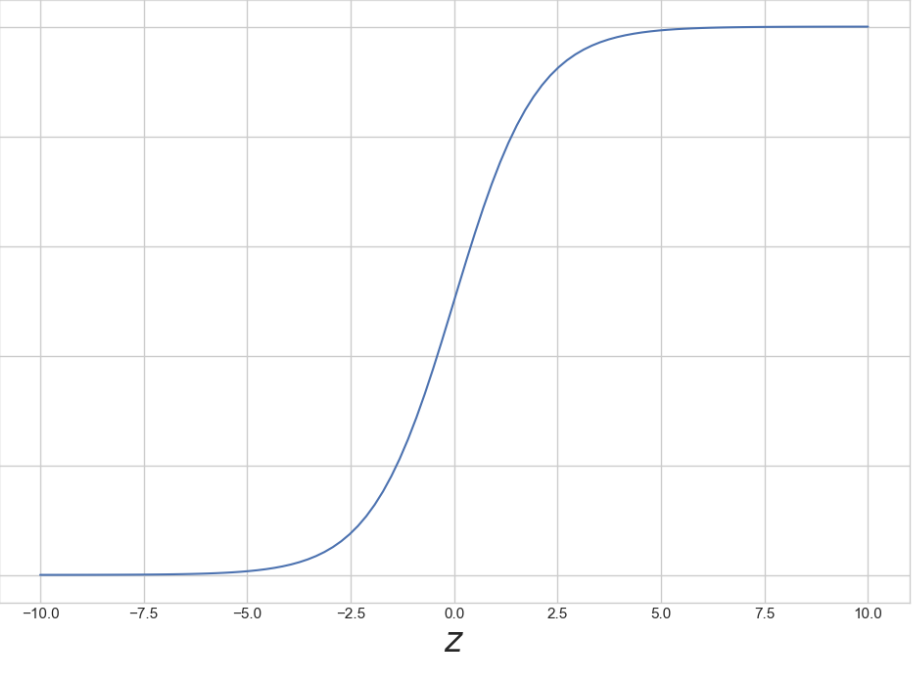
4. 시그모이드 그래프
시그모이드(Sigmoid) 그래프는 S 모양의 곡선 형태를 가지는 함수 그래프이다.
주로 로지스틱 함수(Logistic function)라고 불리며 실수 입력을 받아
0과 1사이의 출력 값 반환한다.
1. S 모양 곡선
- 시그모이드 함수의 그래프는 S 모양의 곡선으로, 입력 값이 음수로 크게 작아지거나 양수로 커질수록 출력 값이 0 또는 1에 가까워진다.
- 0과 1 사이의 출력
- 시그모이드 함수는 항상 0과 1 사이의 값을 출력한다.. 이러한 특성 때문에 이를 이진 분류(binary classification) 문제에서 확률 값으로 사용하는 데 매우 적합하다.
- 미분가능
- 시그모이드 함수는 연속하며 미분 가능한 함수로, 미분 값을 쉽게 계산할 수 있다. 이 특성은 경사 하강법과 같은 최적화 알고리즘에서 유용하게 사용된다.
- 로지스틱 회귀
- 시그모이드 함수는 로지스틱 회귀 모델에서 활성화 함수로 사용되며 이진 분류 모델에서 확률 값을 예측하는 데 활용
#시그모이드는 0과 1사이를 넘어가지 않는다. 0~1사이의 값을 가진다.*********
z = np.linspace(-10, 10, 100)
sigma = 1/(1+np.exp(-z))
plt.figure(figsize=(12,8))
plt.plot(z, sigma)
plt.xlabel('$z$', fontsize=25)
plt.ylabel('$\sigma(z$)', fontsize=25)
plt.show()5. 다변수 벡터
다변수 벡터(Multivariate Vector Function): 하나 이상의 입력 변수를 가지며 입력 변수들을 처리하여 하나 이상의 출력 벡터를 생성하는 함수를 나타낸다.
- 용도
- 머신러닝 및 데이터 분석 작업에서 사용된다.
2.ex) 다차원 입력 데이터를 받고 다차원 출력 데이터를 생성하는 신경망은 벡터함수의 예시이다.- 복잡한 입력과 출력 관계를 모델링하고, 예측, 분류, 회귀 등 작업 수행
1. 2차원 그리드 생성
import numpy as np
#입력받은 u와v로(1차원 배열) 2차원 그리드를 생성한다.
u = np.linspace(0, 1, 30)
v = np.linspace(0, 1, 30)
#한꺼번에 계산 meshgrid
U, V = np.meshgrid(u,v)
2. 시각화 (X는 이전 지수 함수 실습에서 만든변수)
fig = plt.figure(figsize=(7, 7))
ax = plt.axes(projection='3d') # 3차원으로 그릴 때 필요한 projection
ax.xaxis.set_tick_params(labelsize=15)
ax.yaxis.set_tick_params(labelsize=15) # 수정된 부분
ax.zaxis.set_tick_params(labelsize=15)
ax.set_xlabel('$x$', fontsize=20)
ax.set_ylabel('$y$', fontsize=20)
ax.set_zlabel('$z$', fontsize=20)
ax.scatter3D(U, V, Z, marker ='.', color = 'gray')
plt.show()
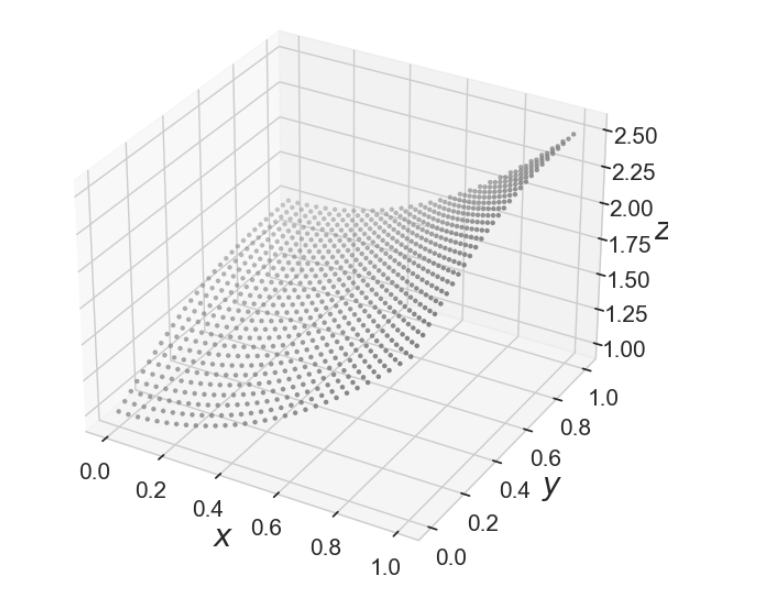
6. 데이터 백분위수
1.
samples = [1, 7, 9, 16, 36, 39, 45, 45, 46, 48, 51, 100, 101]
samples
#출력 [1, 7, 9, 16, 36, 39, 45, 45, 46, 48, 51, 100, 101]
2.
tmp_y = [1]*len(samples) #[1] 단일숫자 --> 출력하면1,1,1,1,1,1,...
tmp_y
# 출력 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
3. 중간값 구하기
import numpy as np
np.median(samples) #중간값 출력
4. 75% 백분위수
np.percentile(samples, 75)
5.
q1 = np.percentile(samples, 25) #백분위수 25찌점 계산
q2 = np.median(samples) #백분위수 중앙값 계산
q3 = np.percentile(samples, 75) #백분위수75% 계산
iqr = q3 - q1 # 사분위 범위 계산 (q3-q1 즉 중간값 50% 범위를 구한다.)
#이상치 검출위한 상단과 하단 경계 계산
upper_fence = q3 + iqr*1.5
lower_fence = q1 - iqr*1.5
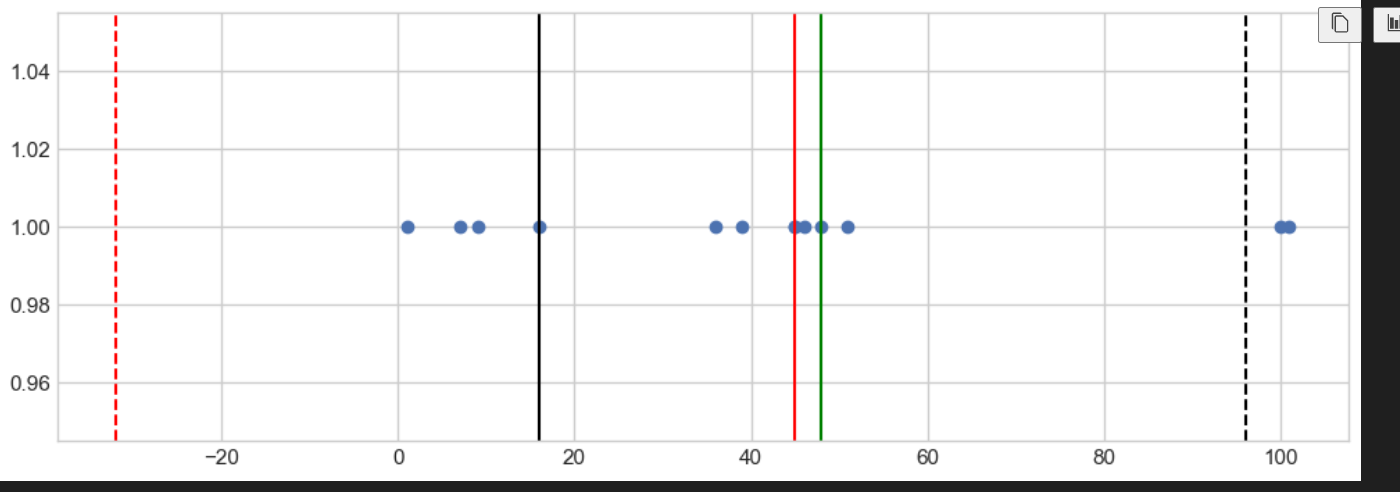
6.백분위수 시각화
plt.figure(figsize=(12,4))
plt.scatter(samples, tmp_y)
plt.axvline(x=q1, color='black')
plt.axvline(x=q2, color='red')
plt.axvline(x=q3, color='green')
plt.axvline(x=upper_fence, color='black', ls='dashed') # 'dashed'로 수정
plt.axvline(x=lower_fence, color='red', ls='dashed') # 'dashed'로 수정
plt.show()
# 그래프에 제일 우측에 있는점을 아웃라이어이라고 한다.
# 검정색 선 부터 초록색선까지가 iqr이다.
#빨강점선과 검정 점선은 iqr의 막대의 1.5배 구간이다.