[BOJ 10849] - A Journey to Greece (DP, 다익스트라, 비트마스킹, 외판원 순회, Python)

보양쿠·2022년 8월 10일

DP boj 다익스트라 비트마스킹 외판원 순회

BOJ

목록 보기

3/260

코드포스 Contest 폭망하고 백준에서 재밌는 문제 찾다가 도전한 문제.
(코드포스에서 맞고 백준에 화풀이 하는 나..?)

문제 자체가 꽤 흥미롭다. 그리고 해외 여행 가고 싶어...

BOJ 10849 - A Journey to Greece 링크
(2022.08.10 기준 난이도 P3)
(치팅 절대 안돼 절대 못해!)

문제

N개의 장소, P개의 꼭 방문해야 하는 장소, M개의 길, 제한 시간 G, 택시 탑승 시 걸리는 시간 T이면,
0부터 시작하여 P를 전부 방문한 뒤 다시 0으로 돌아올 때, 걸리는 최소 시간이 G 이하인지 출력
단, 택시 탑승은 한번만 할 수 있다.

알고리즘

첫눈에 보면 바로 보이는 알고리즘은 바로 '외판원 순회'
그런데 장소의 개수인 N이 20000까지다. 그래서 N 그대로 외판원 순회를 그대로 돌려버리면.. 메모리가 그냥 펑
그래서 시작하는 장소인 0과 꼭 방문해야 하는 P개의 장소들을 따로 좌표 압축 느낌으로 0부터 차례대로 정렬해준 다음, 그 장소들로 하여금 '다익스트라'를 돌려서 방문해야 하는 장소들 간 거리를 구해준다. 그 다음에 외판원 순회 방식으로 DFS를 하면 되는데.. 택시 탑승 유무 때문에 쉽진 않을 것이다..! ㅎㅎ 자세한 풀이는 풀이에서!

다익스트라와 외판원 순회부터 이해를 완벽하게 한 다음, 풀이를 보자.

풀이

처음부터 코드가 진행되는 순서대로 풀이를 해보겠다.
P개의 꼭 방문해야 하는 장소의 위치 pi와 머물러야 하는 시간 ti가 있다.
pi의 범위는 0 ≤ pi < N. 0이 포함된다. 0은 시작하는 정점이므로 방문할 수 밖에 없다. 이를 유의하여 좌표 압축을 해야 하는데, 방법은 여러 가지이다.
나 같은 경우는 아래 코드처럼 하였다.
site = {0: 0}
stay = zero = 0
for i in range(1, P + 1):
    p, t = map(int, input().split())
    if not p:
        zero += 1
    else: site[p] = i - zero
    stay += t
P = len(site)
방문해야 하는 장소를 site 사전에 담는다고 하면, 0부터 담는다.
그리고 idx가 1부터 시작 되게끔 for문을 돌려 P개의 줄만큼 방문해야 하는 위치와 머물러야 하는 시간을 입력 받는다.
이 때, 위치가 0이 나오면 site 사전에 담을 필요가 없다. 왜냐 하면, 0이란 위치의 정보는 이미 site 사전에 있기 때문. 그러므로 0이 나왔다는 flag만 활성화 해준다.
이 이후로 site에 담을 때 idx는 1을 낮춰야 한다. 0이란 위치를 건너 뛰었기 때문.
그러므로 flag가 활성화되면 idx - 1을 site 사전에 담으면 된다.
그리고 P는 site 사전 개수만큼 초기화.

그리고 stay는 머물러야 하는 시간을 담은 건데, 이는 그냥 한번 방문했을 때 머무르는 시간이므로 전부 더해놓았다가 나중에 외판원 순회 결과에 더해주면 된다.

다음은 평범한 다익스트라 알고리즘과 같다.
N개 정점이 있는 빈 그래프를 만들어주고 M개의 간선만큼 정보를 입력 받는다. 이 때, 간선들은 양방향이다.
그리고 P개의 장소 간 거리를 구해야 한다.
방법은 여러 가지겠지만 비슷할 것이다.
나 같은 경우는 아래 코드와 같다.
for p, i in site.items():
    distance = [inf] * N
    distance[p] = 0
    queue = []
    heapq.heappush(queue, [0, p])
    while queue:
        d, present = heapq.heappop(queue)
        if distance[present] < d:
            continue
        for nxt, dd in graph[present]:
            if distance[nxt] > distance[present] + dd:
                distance[nxt] = distance[present] + dd
                heapq.heappush(queue, [distance[nxt], nxt])
    for q, j in site.items():
        result = distance[q]
        matrix[i][j] = result
        matrix[j][i] = result
site의 위치 순서대로 다익스트라를 돌린다.
돌릴 때는 실제 위치 값으로 돌리고
P개의 장소 간 거리를 담을 땐, 좌표 압축 값을 넣으면 된다.

사실 최적화를 더 해주자면, site의 마지막 위치는 하지 않아도 된다. 양방향으로 담으면 전 과정에서 마지막 위치 까지의 거리가 전부 담기기 때문. ~~근데 귀찮아~~

자 이제 대망의 마지막 "외판원 순회"가 남았다.

택시 탑승은 한번만 가능하다.
여기서 여러 생각이 들 것이다.

첫번째는
'T보다 큰 거리를 하나씩 T로 바꾸면서 해볼까?'
시간 초과다.

두번째는
'최소 시간인 순회 경로에서의 가장 긴 거리를 저장하여 T랑 비교해볼까?'
그럴 듯하다. 하지만 틀렸다. ~~(나의 첫번째 시도 방법)~~
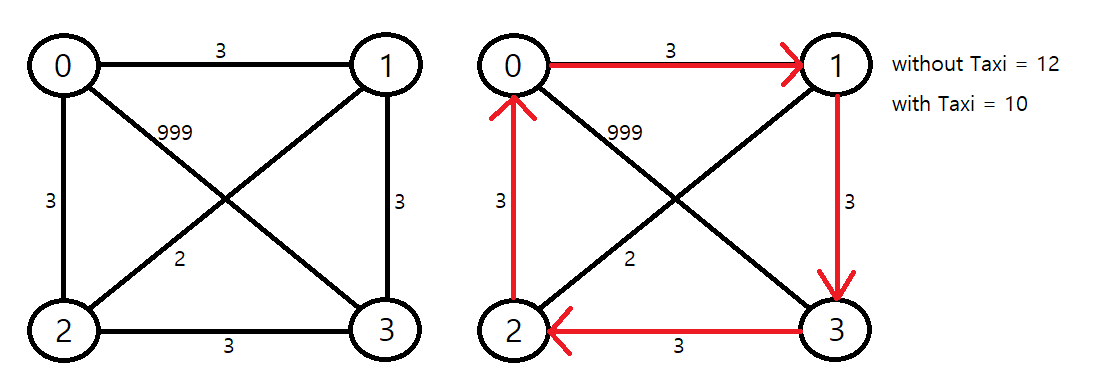
하나의 예시를 들어보면

왼쪽 그림과 같은 그래프가 있고 T = 1 이면
외판원 순회를 하면 오른쪽 그림과 같이 경로를 찾을 것이다. (경로는 여러 개일 수 있지만 최소 시간은 같다.)
택시 없이는 12가 걸리고 택시를 타면 10이 걸린다. (경로 중 간선의 최대 거리가 3이므로 2만큼 줄어든다.)
만약, 가장 긴 거리를 저장하는 방식을 사용했다면 이렇게 답이 나오겠지만...
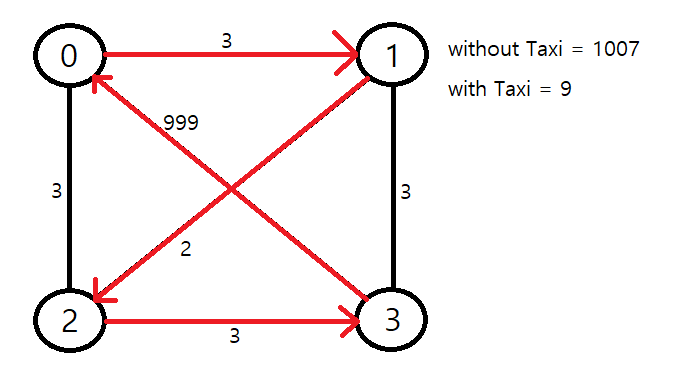
이런 경로가 있을 수 있다.
택시를 타게 되면 9가 나온다.
만약에 최대로 머무를 수 있는 시간 G가 9였다면
정답은 'possible with taxi' 이지만
가장 긴 거리를 저장하는 방식을 사용한다면 출력은 'impossible' 이 나온다.

그럼 어떻게 해야 할까?
먼저 기본적인 외판원 순회는 dp 값 하나만 반환한다.
하지만 여기서의 외판원 순회는 값이 두 개를 반환해야 한다.
이를 다르게 말하면 dp에 차원을 하나 더 추가해야 한다는 것이다.
def dfs(p, v):
    if v == (1 << P) - 1:
        return [matrix[p][0], T]
    if dp[p][v][0] > -1:
        return dp[p][v]
    dp[p][v] = [inf, inf]
    for q in range(P):
        if not v & (1 << q):
            notTaxi, taxi = dfs(q, v | (1 << q))
            dp[p][v][0] = min(dp[p][v][0], matrix[p][q] + notTaxi)
            dp[p][v][1] = min(min(dp[p][v]), matrix[p][q] + taxi, T + notTaxi)
    return dp[p][v]
dp가 삼차원이 되었다.
dp[p][v][0]은 택시를 타지 않은 경로 정보
dp[p][v][1]은 택시를 탄 경로 정보

기본적인 틀은 외판원 순회와 같다.

전부 방문하였으면 (if v == (1 << P) - 1:)
0으로 돌아가는 거리와 T를 반환한다.

그리고 dp 값이 존재하면 dp 그대로 반환한다.

1번과 2번에 해당하지 않으면 다음 가능한 장소를 탐색을 할 것인데
여기서 dfs 함수의 반환값을 notTaxi, taxi에 받는다. 그리고 dp[p][v][0] 에는 원래 외판원 순회처럼 값을 넣는다. 문제는 dp[p][v][1]이다.

택시를 탔을 때의 최소 거리(시간)는 타지 않았을 때와 탔을 때. 둘 다 고려해야 한다.
'p->q, 택시를 타지 않았을 때의 거리'와 taxi(q->끝, T를 고려한 거리)를 합치면 'p->끝, T를 고려한 거리'가 된다.
또한, 'p->q, 택시를 탄 거리'와 notTaxi(q->끝, 택시를 타지 않은 거리)를 합치면 'p->끝, 택시를 탄 거리'가 된다.
이 두 거리와 dp 값(타지 않았을 때와 탔을 때. 둘 다)를 비교하여 최소값으로 dp[p][v][1]을 갱신해주면 된다.

'T를 고려한 거리'라고 표현한 이유는 꼭 택시를 타지 않았을 수도 있기 때문이다. (하지만 T를 고려하여 정한 거리이기 때문)

이 코드 대장정(?)을 마치면 답이 나온다.

코드

import sys; input = sys.stdin.readline
import heapq
from math import inf

# 외판원 순회 함수
def dfs(p, v):
    if v == (1 << P) - 1:
        return [matrix[p][0], T]
    if dp[p][v][0] > -1:
        return dp[p][v]
    dp[p][v] = [inf, inf]
    for q in range(P):
        if not v & (1 << q):
            notTaxi, taxi = dfs(q, v | (1 << q))
            dp[p][v][0] = min(dp[p][v][0], matrix[p][q] + notTaxi)
            dp[p][v][1] = min(min(dp[p][v]), matrix[p][q] + taxi, T + notTaxi)
    return dp[p][v]

N, P, M, G, T = map(int, input().split())

# 방문해야 하는 정점들을 입력 받고 좌표 압축 및 P 초기화
site = {0: 0}
stay = zero = 0
for i in range(1, P + 1):
    p, t = map(int, input().split())
    if not p:
        zero += 1
    else: site[p] = i - zero
    stay += t
P = len(site)

# 간선을 입력 받아 graph 만들기 (간선은 양방향)
graph = [[] for _ in range(N)]
for _ in range(M):
    a, b, c = map(int, input().split())
    graph[a].append((b, c))
    graph[b].append((a, c))

# P개의 정점들 간 거리를 담을 행렬을 만들고
# P개의 정점 차례대로 다익스트라를 돌려 행렬에 거리 입력
matrix = [[0] * P for _ in range(P)]
for p, i in site.items(): # 다익스트라할 땐 실제 위치 사용
    distance = [inf] * N
    distance[p] = 0
    queue = []
    heapq.heappush(queue, [0, p])
    while queue:
        d, present = heapq.heappop(queue)
        if distance[present] < d:
            continue
        for nxt, dd in graph[present]:
            if distance[nxt] > distance[present] + dd:
                distance[nxt] = distance[present] + dd
                heapq.heappush(queue, [distance[nxt], nxt])
    for q, j in site.items(): #거리 담을 땐 압축 값 사용
        result = distance[q]
        matrix[i][j] = result
        matrix[j][i] = result

# dp는 3차원으로 만들어야 함
# 현재 위치, 방문한 위치, 택시 고려 유무
dp = [[[-1] * 2 for _ in range(1 << P)] for __ in range(P)]
notTaxi, taxi = dfs(0, 1 << 0)
# 답을 출력할 때, stay 값을 꼭 더해줘야 한다.
print('possible without taxi') if notTaxi + stay <= G else print('possible with taxi') if taxi + stay <= G else print('impossible')

여담

문제가 재밌어 보여서 풀다가 택시 탑승 유무 때문에 골머리 싸맨 문제.
그래도 서칭 전혀 안하고 내 머리 100%로 풀었다. 휴..

그리고 Python 3는 내가 처음으로 AC를 받았다.
걸린 시간 보면 7.8초 ㅋㅋㅋㅋㅋㅋㅋㅋㅋ
파이썬 너란 녀석.. 너무 무거운 언어야...

마지막으로..
나도 산토리니 가보고 싶어...