BOJ 16974 - 레벨 햄버거 링크
(2023.07.26 기준 S1)

문제

레벨-L 버거는 햄버거번, 레벨-(L-1) 버거, 패티, 레벨-(L-1)버거, 햄버거번으로 이루어져 있으며, 레벨-0 버거는 패티로만 이루어져 있다.

레벨-N 버거를 시켰을 때, 아래 X장에 포함된 패티의 수 출력

알고리즘

DP and DNC

풀이

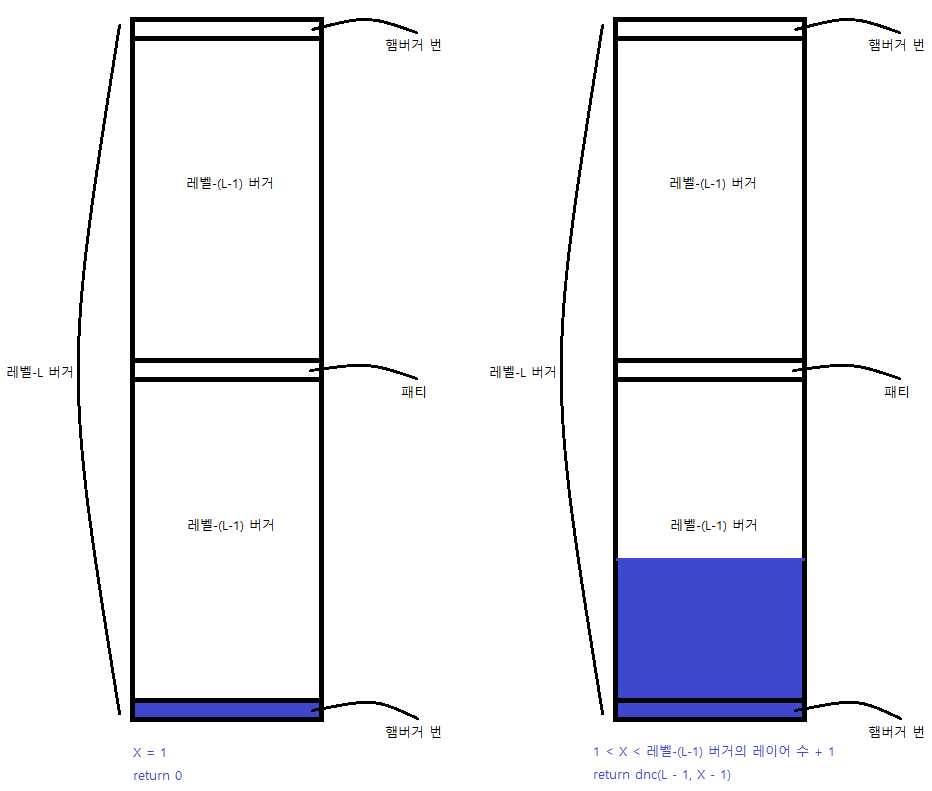
레벨-L 버거는 다음과 같이 쌓여져 있다.

X 값에 따라 분할 정복을 하면 되는데, 각 구간 별로 나눌 수 있다.

각 레벨마다 레이어 수와 패티 수는 처음에 DP로 구해놓자.

코드

• C++

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

const int MAXN = 50;

ll dp1[MAXN], dp2[MAXN]; // 레이어의 수, 패티의 개수

// 햄버거는 [번, N-1 버거, 패티, N-1 버거, 번] 구간으로 이루어져 있으므로
// X에 따라 분할 정복을 하자.
ll dnc(int N, ll X){
    // 현재 먹어야 하는 장수가 1장이면 패티는 0장이다.
    if (X == 1) return 0;

    // 현재 먹어야 하는 장수가 번과 N-1버거 미만이면
    // 맨 앞 번을 빼고 분할 정복
    if (X < dp1[N - 1] + 1) return dnc(N - 1, X - 1);

    // 현재 먹어야 하는 장수가 번과 N-1버거이면
    // N-1버거의 패티 수다.
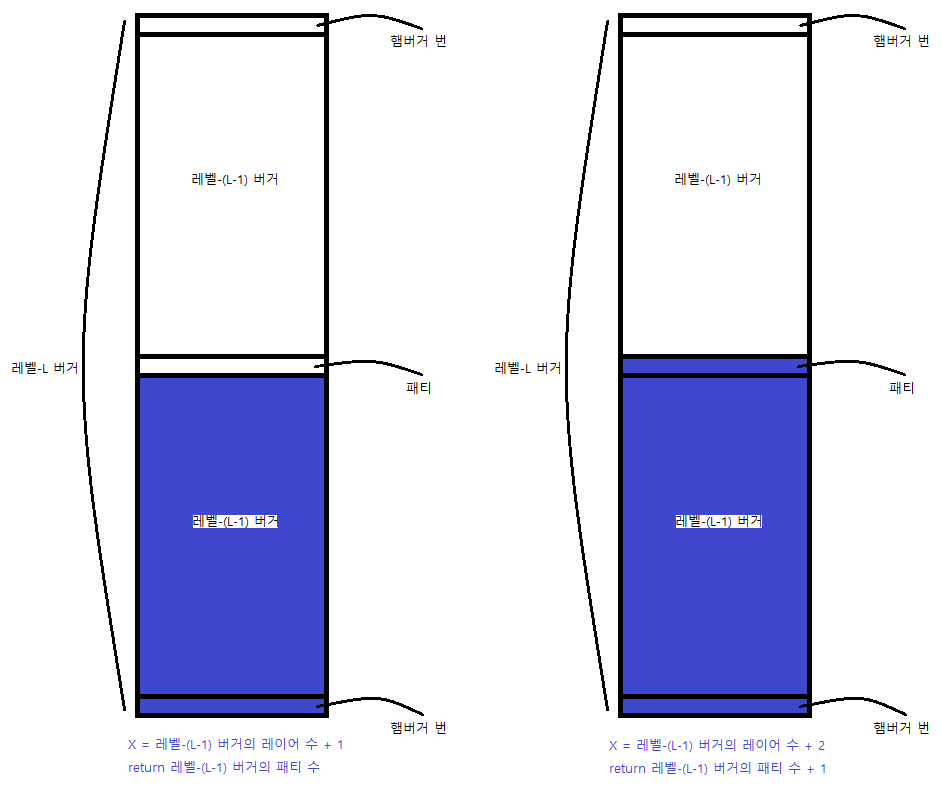
    if (X == dp1[N - 1] + 1) return dp2[N - 1];

    // 현재 먹어야 하는 장수가 번과 N-1버거와 패티이면
    // N-1버거의 패티 수 + 1이다.
    if (X == dp1[N - 1] + 2) return dp2[N - 1] + 1;

    // 현재 먹어야 하는 장수가 번과 N-1버거와 패티와 N-1버거 미만이면
    // 첫 N-1버거의 패티 수 + 중간 패티 한장 + 나머지 뒷부분 분할 정복 결과다.
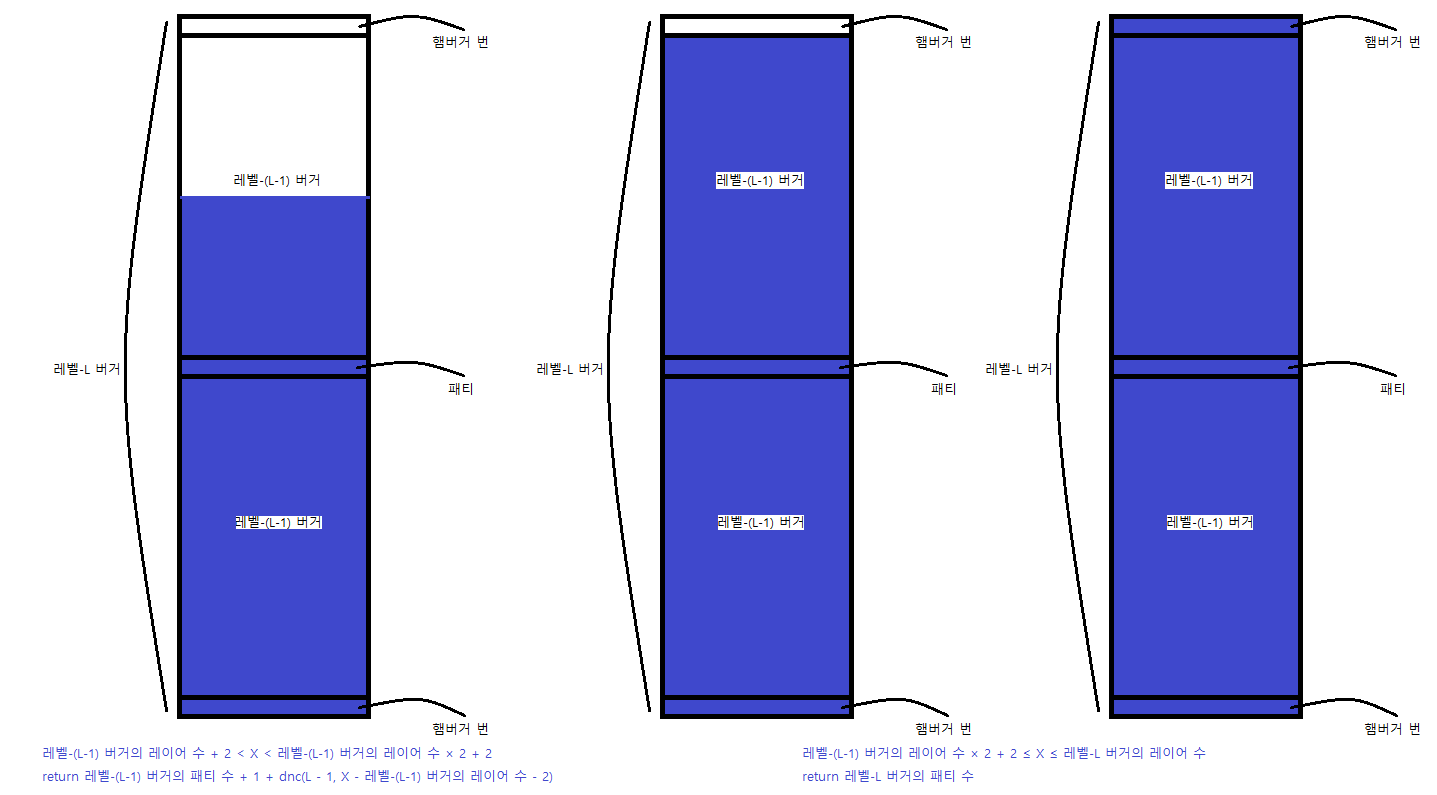
    if (X < dp1[N - 1] * 2 + 2) return dp2[N - 1] + 1 + dnc(N - 1, X - dp1[N - 1] - 2);

    // 현재 먹어야 하는 장수가 N버거 레이어 수와 동일하거나 1 작다면
    // N버거의 패티 수다.
    return dp2[N];
}

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    int N; ll X;
    cin >> N >> X;

    dp1[0] = dp2[0] = 1; // 레벨-0 버거는 패티만으로 이루어져 있다.

    // 레벨-L 버거는 햄버거번, 레벨-(L-1) 버거, 패티, 레벨-(L-1)버거, 햄버거번으로 이루어져 있다.
    for (int i = 1; i <= N; i++){
        dp1[i] = dp1[i - 1] * 2 + 3;
        dp2[i] = dp2[i - 1] * 2 + 1;
    }

    cout << dnc(N, X);
}

• Python

import sys; input = sys.stdin.readline

# 햄버거는 [번, N-1 버거, 패티, N-1 버거, 번] 구간으로 이루어져 있으므로
# X에 따라 분할 정복을 하자.
def dnc(N, X):
    # 현재 먹어야 하는 장수가 1장이면 패티는 0장이다.
    if X == 1:
        return 0

    # 현재 먹어야 하는 장수가 번과 N-1버거 미만이면
    # 맨 앞 번을 빼고 분할 정복
    if X < dp1[N - 1] + 1:
        return dnc(N - 1, X - 1)

    # 현재 먹어야 하는 장수가 번과 N-1버거이면
    # N-1버거의 패티 수다.
    if X == dp1[N - 1] + 1:
        return dp2[N - 1]

    # 현재 먹어야 하는 장수가 번과 N-1버거와 패티이면
    # N-1버거의 패티 수 + 1이다.
    if X == dp1[N - 1] + 2:
        return dp2[N - 1] + 1

    # 현재 먹어야 하는 장수가 번과 N-1버거와 패티와 N-1버거 미만이면
    # 첫 N-1버거의 패티 수 + 중간 패티 한장 + 나머지 뒷부분 분할 정복 결과다.
    if X < dp1[N - 1] * 2 + 2:
        return dp2[N - 1] + 1 + dnc(N - 1, X - dp1[N - 1] - 2)

    # 현재 먹어야 하는 장수가 N버거 레이어 수와 동일하거나 1 작다면
    # N버거의 패티 수다.
    return dp2[N]

N, X = map(int, input().split())

dp1 = [0] * (N + 1) # 레이어의 수
dp2 = [0] * (N + 1) # 패티의 개수
dp1[0] = dp2[0] = 1 # 레벨-0 버거는 패티만으로 이루어져 있다.

# 레벨-L 버거는 햄버거번, 레벨-(L-1) 버거, 패티, 레벨-(L-1)버거, 햄버거번으로 이루어져 있다.
for i in range(1, N + 1):
    dp1[i] = dp1[i - 1] * 2 + 3
    dp2[i] = dp2[i - 1] * 2 + 1

print(dnc(N, X))