BOJ 17831 - 대기업 승범이네 링크
(2023.07.31 기준 P5)
문제
N명의 직원이 있고, 사장을 제외한 모든 직원에겐 사수가 한 명씩 배정된다.
사수와 부사수 관계에 있는 두 직원을 멘토링 관계로 만들 수 있고, 각 직원마다 수치화된 실력이 있는데, 멘토링 관계에서 발생하는 시너지는 두 직원의 실력의 곱과 같다.각 직원은 최대 1개의 멘토링 관계에 포함될 수 있다면, 모든 멘토링 관계에서 발생하는 시너지의 합의 최대 출력
알고리즘
트리에서의 DP
풀이
문제는 결국 트리 상의 모든 정점은 인접한 정점끼리 하나의 페어를 맺을 수 있고, 정점 하나 당 하나 이하의 페어에 포함될 수 있다. 모든 페어의 두 정점의 가중치 곱의 합이 최대로 만드는 것이다.
중요한 것은, 각 정점마다 하나의 페어에 포함되느냐이다.
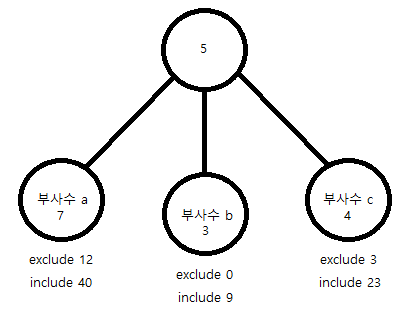
그러므로 dp[node][include]로 놓고 채워나갈 것이다.일단, 문제에 나오는 그림이자 두번째 예제인 트리를 루트 직전까지 계산해보자. 눈으로 머리로 계산해도 쉽다.
그러면 이렇게 나온다.이제 루트의 exclude부터 구해보자.
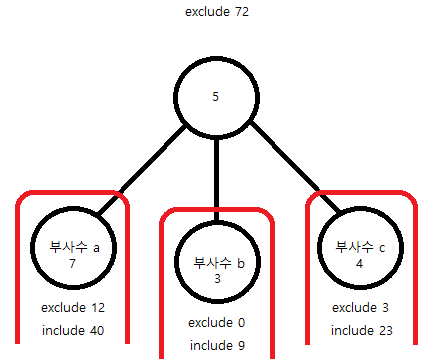
루트가 페어에 포함되지 않으면 루트의 부사수들은 페어에 포함이 되건 포함이 되지 않건 상관없다.
그러므로 부사수들마다 계산된 dp값 중 최댓값들을 더하면 루트의 exclude 값이 된다.
이렇게 말이다. 루트의 exclude 값은 72다.이제 루트의 include를 구해야 한다.
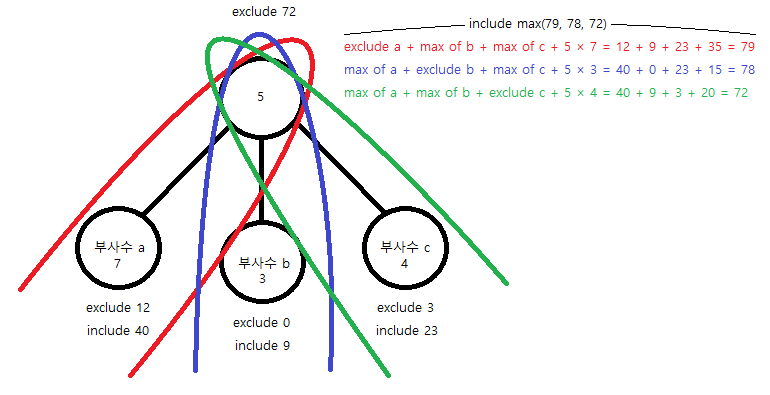
만약, 루트가 부사수 a와 페어를 맺는다면? 부사수 a는 직전까지 페어에 포함된 적이 없어야 하며, 부사수 b, c는 상관없다. 결국은, (exclude a + max(dp[b]) + max(dp[c]) + 5×7(가중치곱))이 부사수 a와 페어를 맺을 때의 include 값이 된다.위와 같이 모든 부사수들과 페어를 맺어보면서 값을 구해 그 중 최댓값이 include 값이 된다.
근데 잘 생각을 해보자. exclude 값은 부사수들의 최댓값을 더한 것이며, include 값은 페어를 맺는 부사수를 제외한 모든 최댓값을 더해야 한다.
그러니, exclude 값에서 맺는 부사수의 최댓값을 빼고 부사수의 exclude 값과 가중치 곱을 더하면 include 값이 된다.
코드
- C++
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 200000;
int A[MAXN], dp[MAXN][2];
vector<int> graph[MAXN];
void dfs(int i){
// i가 포함되지 않은 최댓값은 부사수들의 시너지 최댓값의 합이다.
for (auto j: graph[i]){
dfs(j);
dp[i][0] += max(dp[j][0], dp[j][1]);
}
// i가 포함되는 최댓값은 부사수 하나하나 엮어보면 된다.
// 부사수 j가 포함되지 않은 시너지 최댓값 + i와 j의 시너지 값
for (auto j: graph[i])
dp[i][1] = max(dp[i][1], dp[i][0] - max(dp[j][0], dp[j][1]) + dp[j][0] + A[i] * A[j]);
}
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
int N; cin >> N;
for (int j = 1, i; j < N; j++){
cin >> i;
graph[--i].push_back(j);
}
for (int i = 0; i < N; i++) cin >> A[i];
fill(&dp[0][0], &dp[N - 1][2], 0); // dp[node][include]
dfs(0);
cout << max(dp[0][0], dp[0][1]);
}- Python
import sys; input = sys.stdin.readline
sys.setrecursionlimit(222222)
def dfs(i):
# i가 포함되지 않은 최댓값은 부사수들의 시너지 최댓값의 합이다.
for j in graph[i]:
dfs(j)
dp[i][0] += max(dp[j])
# i가 포함되는 최댓값은 부사수 하나하나 엮어보면 된다.
# 부사수 j가 포함되지 않은 시너지 최댓값 + i와 j의 시너지 값
for j in graph[i]:
dp[i][1] = max(dp[i][1], dp[i][0] - max(dp[j]) + dp[j][0] + A[i] * A[j])
N = int(input())
graph = [[] for _ in range(N)]
for j, i in enumerate(map(int, input().split())):
graph[i - 1].append(j + 1)
A = list(map(int, input().split()))
dp = [[0] * 2 for _ in range(N)] # dp[node][include]
dfs(0)
print(max(dp[0]))