Educational Codeforces Round 133 (Div. 2) - Robot in a Hallway 링크
(2022.08.29 기준 Difficulty *2000)
(No cheating Yes study)

문제

2개의 행과 m개의 열로 이루어진 행렬 M이 있고, M(i, j) 만큼의 시간이 지나야 (i, j)에 방문할 수 있으며 한번 방문한 곳은 다시 방문할 수 없을 때
로봇이 (1, 1) 에서 시작하여 모든 곳을 방문할 수 있는 최소 시간

알고리즘

먼저 로봇이 움직이는 경로를 구현해야 한다. 풀이에서 후술하겠지만 움직이는 방법이 정해져 있으므로, 그걸 먼저 찾아내야 한다.
그 다음은, 어느 한 곳에 다다를 때마다 그 곳이 방문한 적이 있으면 더 이상 진행하지 않도록 메모이제이션 기법을 써주자. (dp)

풀이

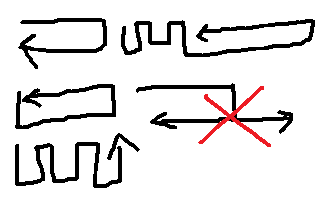
로봇이 갈 수 있는 경로를 그려보았다.
로봇이 갈 수 있는 방법은 처음부터 직선으로 가던지, 지그재그로 쭉 가던지, 지그재그로 가다가 직선으로 쭉 가야 한다.
그림에 빨간 엑스 쳐져 있는 방법은 직선으로 가다가 지그재그를 위해 중간에 내려가는 방법인데, 이는 불가능하다. 왜냐면, 행이 두 개 밖에 없고 한번 방문한 곳은 다시 방문할 수 없기 때문이다.

그러므로
1. 왼쪽 위 -> 오른쪽 위 -> 오른쪽 밑 -> 왼쪽 밑
2. 왼쪽 위 -> 왼쪽 밑 -> 오른쪽 밑 -> 오른쪽 위 -> 왼쪽 위
3. 끝까지 지그재그
이 방법들로 하여금, 각각 최소 시간을 담은 배열을 만들고

각 위치마다 지그재그로 가다가 직선으로 가는 방법의 최소 시간을 구해 출력 값을 갱신해주면 된다.

갱신해줄 때 주의해야 할 점은
열 번호가 홀수이냐 짝수이냐에 따라 방향과 배열의 끝 부분을 잘 지정해야 하고
최소 시간 값을 그 위치에서에서 구하는 부분까지의 시간 값도 같이 구해 비교해주어야 한다.

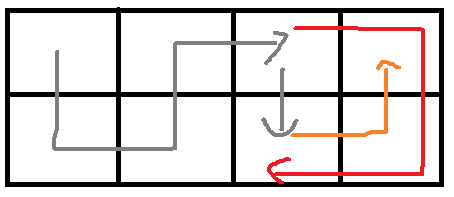
그림처럼 m = 4이고 2열에서 최소 시간을 구하고 있다고 생각해보자.
(0, 2)에선 빨간색 방향을 구하면 된다.

time(0, 2) = max(1번방법(1, 2), 3번방법(0, 2) + 3)

(1, 2)에선 주황색 방향을 구하면 된다.

time(1, 2) = max(2번방법(0, 3), 3번방법(1, 2) + 2)

이렇게 구해진 time들과 answer를 비교하여 젤 작은 값으로 answer를 갱신해주면 된다.

이를 식으로 나타내면 (편의상 j를 열이라고 생각하자)

if j가 홀수:
	time_1 = max(2번방법(0, j), 3번방법(1, j) + (m - j - 1) * 2 + 1)
    time_2 = max(1번방법(1, j + 1), 3번방법(0, j) + (m - j - 1) * 2)
if j가 짝수:
	time_1 = max(1번방법(1, j), 3번방법(0, j) + (m - j - 1) * 2 + 1)
    time_2 = max(2번방법(0, j + 1), 3번방법(1, j) + (m - j - 1) * 2)
answer = min(answer, time_1, time_2)

그리고 1번, 2번 방법의 배열을 만들 때 마지막에 -inf 값을 넣어야 한다.
지그재그로 끝까지 갔고 또한, 더이상 앞으로 나아갈 직선 방향이 없기 때문에 -inf를 넣으면 max 함수에서 알아서 걸러진다.

코드

import sys; input = sys.stdin.readline
from math import inf

for _ in range(int(input())):
    m = int(input())
    M = [list(map(int, input().split())) for _ in range(2)]
    up = [[0] * m for _ in range(2)] # 1번 방법
    down = [[0] * m for _ in range(2)] # 2번 방법
    zigzag = [[0] * m for _ in range(2)] # 3번 방법
    
    # 각 방법 별로 배열을 만든다. +1 하는 이유는 "행렬 값의 초가 지나야" 방문 가능.
    down[1][0] = M[1][0] + 1
    zigzag[1][0] = M[1][0] + 1
    for j in range(1, m):
        if j % 2:
            zigzag[1][j] = max(zigzag[1][j - 1], M[1][j]) + 1
            zigzag[0][j] = max(zigzag[1][j], M[0][j]) + 1
        else:
            zigzag[0][j] = max(zigzag[0][j - 1], M[0][j]) + 1
            zigzag[1][j] = max(zigzag[0][j], M[1][j]) + 1
        up[0][j] = max(up[0][j - 1], M[0][j]) + 1
        down[1][j] = max(down[1][j - 1], M[1][j]) + 1
    up[1][-1] = max(up[0][-1], M[1][-1]) + 1
    down[0][-1] = max(down[1][-1], M[0][-1]) + 1
    for j in range(m - 2, -1, -1):
        up[1][j] = max(up[1][j + 1], M[1][j]) + 1
        down[0][j] = max(down[0][j + 1], M[0][j]) + 1
    up[0].append(-inf)
    up[1].append(-inf)
    down[0].append(-inf)
    down[1].append(-inf)
    
    # 첫번째 열에선 따로 구해준다.
    answer = min(up[1][0], max(down[0][1], zigzag[1][0] + (m - 1) * 2))
    
    # 각 열 별로 정답을 갱신
    for j in range(1, m):
        if j % 2:
            answer = min(answer, max(down[0][j], zigzag[1][j] + (m - j - 1) * 2 + 1), max(up[1][j + 1], zigzag[0][j] + (m - j - 1) * 2))
        else:
            answer = min(answer, max(up[1][j], zigzag[0][j] + (m - j - 1) * 2 + 1), max(down[0][j + 1], zigzag[1][j] + (m - j - 1) * 2))
    print(answer)

여담

갑자기 확 어려워지는 난이도. 대회 당시에는 어떻게 코드를 짜야 할지 다 생각이 됐는데, dp 부분에서 코드로 풀어내지를 못해서 아쉽게도....
역시 난이도 2000