Educational Codeforces Round 133 (Div. 2) - Chip Move 링크
(2022.08.29 기준 Difficulty *2000)
(No cheating Yes study)

문제

이동할 때 0에서 시작하고 양의 정수만큼 가야 하며, 1번째 이동의 길이는 k, 2번째 이동의 길이는 k+1, 3번째 이동은 k+2 ... a번째 이동의 길이는 k+a-1만큼 나눌 수 있어야 한다고 할 때
1 ~ n 각 위치에 도착할 수 있는 방법의 수

알고리즘

어떤 한 점에 도착하는 방법은 0에서 한번에 갈 수도 있고 다른 점에서 갈 수도 있다. 이 모든 방법을 하나하나 찾을 수 없으므로 dp를 사용.
그리고 k, k + 1, k + 2 ... k + a - 1 이런 식으로 이동하기 때문에 모듈러 연산을 해야 한다.

풀이

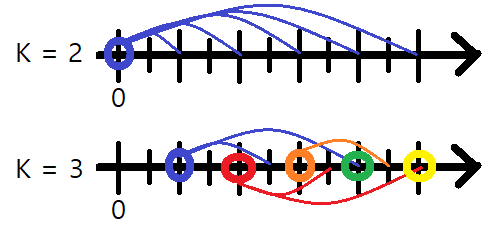
두번째 예제인 n = 10, k = 2인 경우일 때를 살펴보자.
시작은 0이다. 그리고 이동이 k로 나눌 수 있다는 것은 k의 배수만큼 움직일 수 있다는 말이다. 그러므로 그림의 첫번째 수직선처럼 갈 수 있을 것이다.

다음은 k가 1만큼 증가한다.
그림을 보면 어떻게 이동하는지 바로 이해가 갈 것이다.
여기서 우린 시작점이 아니라 도착점을 살펴볼 것이다.

2~4까지는 도착하는 경로가 없다.
5에 도착하는 경로는 2에서 시작하는 경로 하나다.
6에 도착하는 경로는 없다.
7에 도착하는 경로는 4에서 시작하는 경로 하나다.
8에 도착하는 경로는 2에서 시작하는 경로 하나다.
9에 도착하는 경로는 6에서 시작하는 경로 하나다.
10에 도착하는 경로는 4에서 시작하는 경로 하나다.

이 경로들을 살펴보면 알 수 있는 점은 두 가지가 있다.
첫번째는, 시작점의 최소는 k 만큼 늘어난다.
두번째는, 시작점과 도착점은 (mod k) 값이 같다.

이 두 점을 이용해 시작점의 최소를 갱신해주면서 도착점이 n보다 커지면 루프를 중단해주고 (최적화)
dp 값만큼 (mod k)를 취해 나머지가 나온 횟수를 담은 배열에 저장하고 동시에 나머지 배열[(mod k)] 값 만큼 dp를 갱신해주며 answer를 갱신해준다. 도착점에 도착하는 경로가 한 개가 아닐 수 있기 때문. (동적계획법)

추가 설명

위 예시대로 k = 3이고 시작 최소 값이 2라고 했을 때
k + 2는 n(=10) 을 넘지 않으므로 검사 시작하고
for (i = 2, i < n + 1, i++) 이렇게 루프가 돌아갈 것이다.
i = 2 일 때, mod k 값은 2이다 (2 % 3 = 2)
그러면 mod[2] += dp[2] 과 dp[2] = mod[2]가 동시에 일어난다.
그러면 mod[2]는 1이 되고 dp[2]는 0이 된다.
그러면 answer를 갱신할 때, answer[i] 는 증가하지 않는다.
그 이후로 mod k 값이 2가 될 때마다 answer[i]는 dp[i] 만큼 증가할 것이다.

코드

n, k = map(int, input().split())
answer = [0] * (n + 1)
dp = [1] + [0] * n
MIN = 0 # 최소 시작점
while MIN + k <= n: # 최소 시작점 + k 가 n을 넘으면 루프 중단
    mod = [0 for _ in range(k)] # 나머지가 나오는 횟수 배열
    for i in range(MIN, n + 1):
        dp[i], mod[i % k] = mod[i % k], dp[i] + mod[i % k]
        # 나머지가 나온 횟수에 dp만큼 더하고 dp에는 나머지가 나온 횟수를 대입
        mod[i % k] %= 998244353
        answer[i] += dp[i]
        answer[i] %= 998244353
    MIN += k
    k += 1
print(*answer[1:])

여담

이 문제까지는 그래도 어떻게 풀지 누구든 생각해낼 수 있는 난이도인 것 같다.
문제 자체가 직관적이기 때문.
(하지만 누구나 풀지는 못할 난이도 ㅋㅎㅋㅎ)

근데 다음 문제 E번부터는 좀... 그래... 너무해