4/16 Heap Sort

힙(Heap)

Heap는 완전이진트리 기반 자료구조이다.
여러 개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료구조입니다.
부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰 이진트리를 뜻합니다.
key(부모노드) ≥ key(자식노드) 조건을 항상 성립합니다.
노드의 인덱스
배열로 구현 시 0번째 인덱스가 아니라 1번째 인덱스에서부터 시작됩니다.
왼쪽 자식의 인덱스 = (부모의 인덱스) 2
오른쪽 자식의 인덱스 = (부모의 인덱스) 2 + 1
부모의 인덱스 = (자식의 인덱스) / 2

힙 종류
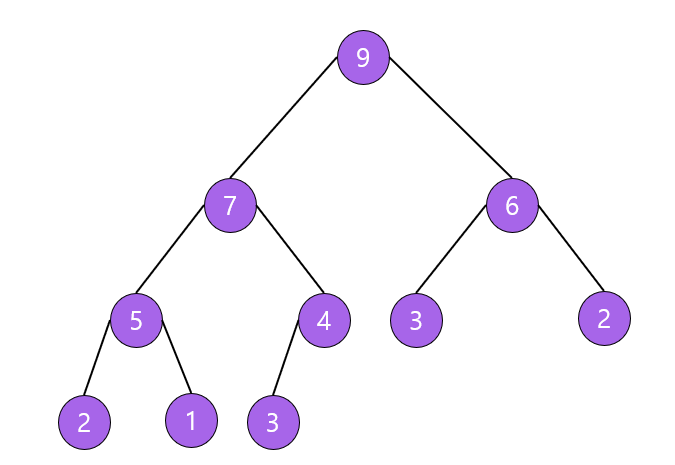
최대 힙(max heap)

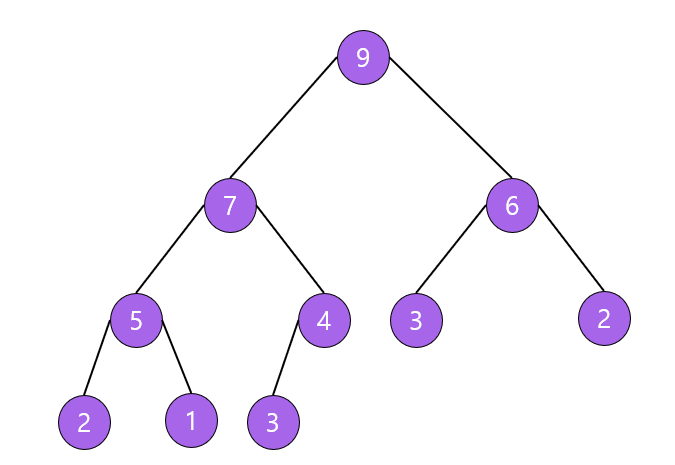
부모 노드의 키값이 자식 노드의 키값보다 크거나 같은 완전 이진 트리
key(부모 노드) ≥ key(자식 노드)

최소 힙(min heap)

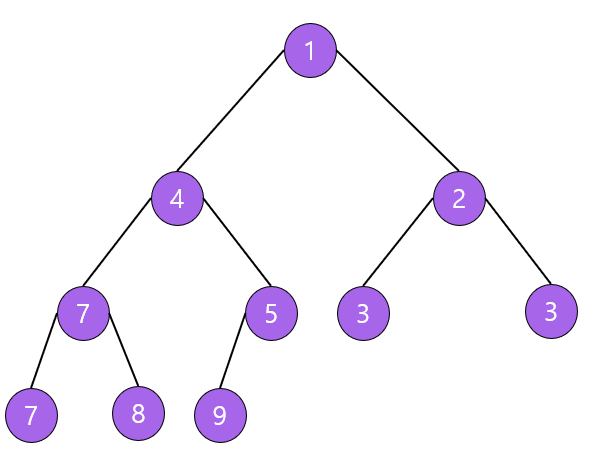
부모 노드의 키값이 자식 노드의 키값보다 작거나 같은 완전 이진 트리
key(부모 노드) ≤ key(자식 노드)

힙 정렬

최대 힙을 이용하면 정렬이 가능합니다.
시간 복잡도: O(nlogn)
불안정 정렬입니다.
과정
최대 힙을 구성
루트를 힙의 마지막 원소와 교환합니다.
마지막 원소를 제외하고 나머지 원소에 대해서 반복합니다.
정렬된 원소를 제외하고 최대 힙에 원소가 1개 남으면 정렬을 종료합니다

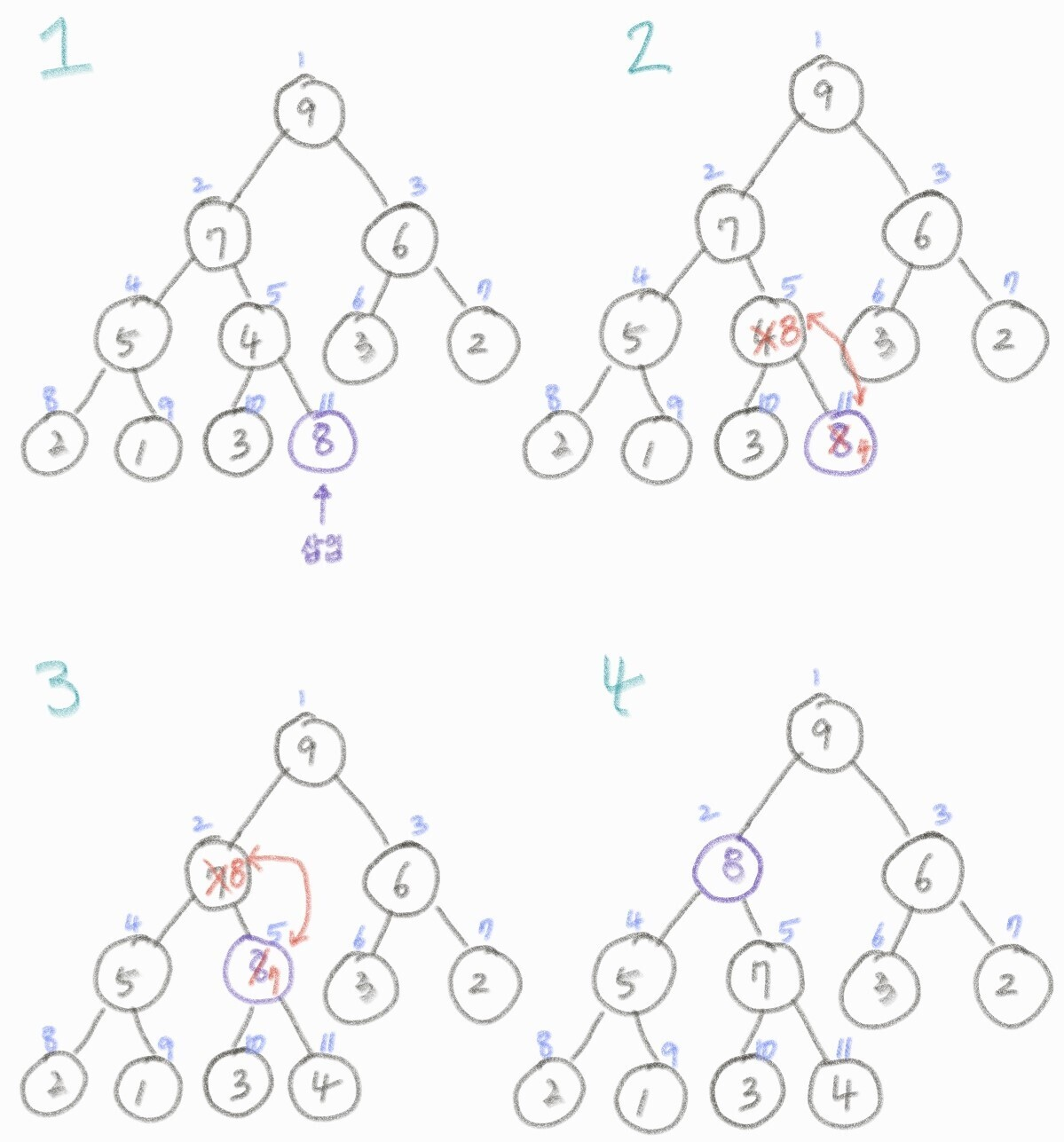
Heat Sort를 구현한 코드입니다.

array = [1, 10, 5, 8, 7, 6, 4, 3, 2, 9]

# 1. 상향식: 특정 노드를 기준으로 위로 올라감
def heap_sort(array):
    n = len(array)
    # heap 구성
    for i in range(n):
        c = i
        while c != 0:
            r = (c-1)//2
            if (array[r] < array[c]):
                array[r], array[c] = array[c], array[r]
            c = r
            print(array)
    # 크기를 줄여가면서 heap 구성
    for j in range(n-1, -1, -1):
        array[0] , array[j] = array[j], array[0]
        r = 0
        c = 1
        while c<j:
            c = 2*r +1
            # 자식 중 더 큰 값 찾기
            if (c<j-1) and (array[c] < array[c+1]):
                c += 1
            # 루트보다 자식이 크다면 교환
            if (c<j) and (array[r] < array[c]):
                array[r], array[c] = array[c], array[r]
            r=c
            print(array)
    print(array)
heap_sort(array)