이번주 퀴즈 문제는 KMP와 보이어 무어를 활용한 문제가 나온다는데 난이도가 있는 알고리즘(KMP가 조금 더 어려움)으로 여력이 있는 사람만 풀면 된다고 하셔서 이론적으로만 공부해볼 생각입니다
KMP 알고리즘
커누스 모리스 프랫 알고리즘(Knuth-Morris-Pratt algorithm)
-
완전 탐색(Brute force)의 시간 복잡도 문제를 해결하기 위한 문자열 탐색 알고리즘
-
길이가 N 인 문자열에서 길이가 M인 문자열을 찾는 과정이라는 가정 하에,
-
Brute force : O(N*M)
-
KMP : O(N+M)
Failure Function, pi
-
찾고자 하는 문자열의 전처리 과정 필요
-
실패 함수(failure function, pi[i])를 만드는 과정
-
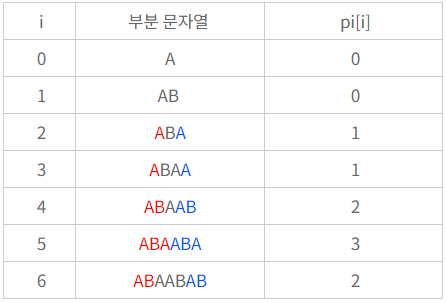
실패 함수: i 번째 위치에서 접두사 == 접미사가 되는 최대 접두사의 길이
-
https://cantcoding.tistory.com/13 에서 전처리 테이블 사진 참조
Python Code
# KMP 알고리즘을 수행하기 전, 패턴을 처리하는 함수
# 패턴의 테이블 생성
def KMP_table(pattern):
lp = len(pattern)
tb = [0 for _ in range(lp)] # 정보 저장용 테이블
pidx = 0 # 테이블의 값을 불러오고, 패턴의 인덱스에 접근
for idx in range(1, lp): # 테이블에 값 저장하기 위해 활용하는 인덱스
# pidx가 0이 되거나, idx와 pidx의 pattern 접근 값이 같아질때까지 진행
while pidx > 0 and pattern[idx] != pattern[pidx]:
pidx = tb[pidx-1]
# 값이 일치하는 경우, pidx 1 증가시키고 그 값을 tb에 저장
if pattern[idx] == pattern[pidx] :
pidx += 1
tb[idx] = pidx
return tbKMP
-
Failure Function 에서 만든 테이블을 활용하여 KMP 알고리즘 진행합니다
-
문자열을 확인할 인덱스 idx, 패턴을 확인할 인덱스 pidx를 분리하여 활용합니다
-
문자열의 idx 번째 문자와 패턴의 pidx 번째 문자가 일치한다면, 두 인덱스를 모두 증가시킵니다
일치하지 않는 경우, pidx-1값을 앞서 생성한 테이블에 적용하여 얼만큼 생략을 하고 진행할 수 있는지 확인합니다. pidx가 0이 되거나, 문자열의 idx번째 문자와 패턴의 pidx번째 문자가 일치할 때 까지 pidx 변경
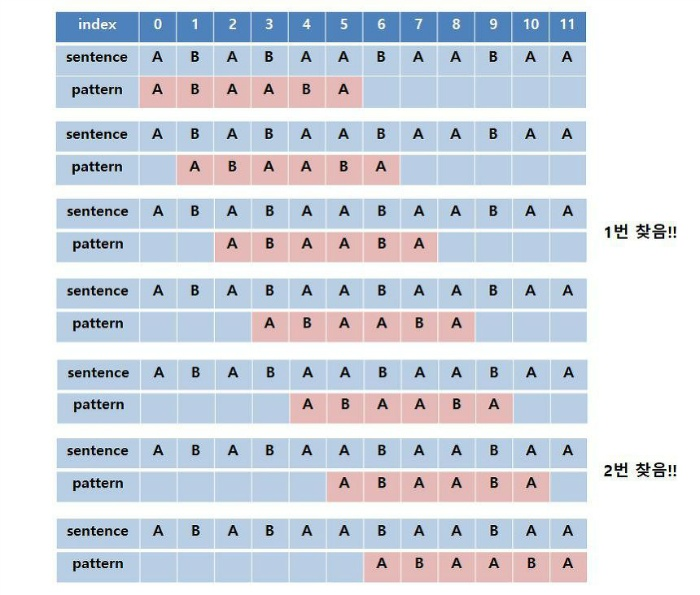
pidx가 패턴의 맨 끝 인덱스에 도달하는 경우가 문자열에서 패턴을 찾은 경우가 됩니다 -
문자열 안에 패턴의 개수가 여러번 나타나는 경우, 이 때의 시작 인덱스를 계산하여 결과 값을 계산하는 리스트에 저장하고, pidx를 테이블 값 기준으로 하여 변경합니다
https://j2wooooo.tistory.com/119 에서 사진 참조
Python Code
- 해당 패턴이 몇 번 나타나는 지, 그 때의 시작 인덱스가 몇인지를 리턴
밑에 써있는 practice 문제를 반영한 코드
def KMP(word, pattern):
# KMP_table 통해 전처리된 테이블 불러오기
table = KMP_table(pattern)
results = [] # 결과를 만족하는 인덱스 시점을 기록하는 리스트
pidx = 0
for idx in range(len(word)):
# 단어와 패턴이 일치하지 않는 경우, pidx를 table을 활용해 값 변경
while pidx > 0 and word[idx] != pattern[pidx] :
pidx = table[pidx-1]
# 해당 인덱스에서 값이 일치한다면, pidx를 1 증가시킴
# 만약 pidx가 패턴의 끝까지 도달하였다면, 시작 인덱스 값을 계산하여 추가 후 pidx 값 table의 인덱스에 접근하여 변경
if word[idx] == pattern[pidx]:
if pidx == len(pattern)-1 :
results.append(idx-len(pattern)+2)
pidx = table[pidx]
else:
pidx += 1
return resultsKMP 알고리즘의 장단점
KMP 알고리즘의 장점
-
일관된 시간 복잡도: KMP 알고리즘은 부분 문자열의 길이와 상관없이 일관된 시간 복잡도를 보장합니다. 이러한 특징으로 인해, 검색 대상 문자열이 매우 긴 경우에도 빠른 검색 속도를 보여줍니다.
-
중복 검색 최소화: KMP 알고리즘은 이전에 매칭된 부분 문자열의 정보를 활용하여 검색하기 때문에, 중복 검색을 최소화할 수 있습니다. 따라서, 문자열 검색 시간을 단축할 수 있습니다.
-
다양한 언어 및 환경에서 사용 가능: KMP 알고리즘은 구현이 비교적 간단하며, 대부분의 프로그래밍 언어 및 환경에서 사용할 수 있습니다.
KMP 알고리즘의 단점
-
추가적인 메모리 사용: KMP 알고리즘은 문자열 검색을 위해 이전에 매칭된 부분 문자열의 정보를 저장하는 배열을 사용하기 때문에, 메모리를 많이 사용하는 경향이 있습니다.
-
전체 문자열 검색에 제한: KMP 알고리즘은 주어진 문자열 내에서 부분 문자열을 검색하는 알고리즘이므로, 전체 문자열이 아닌 일부분만 검색하려는 경우에는 KMP 알고리즘을 사용할 수 없습니다.
-
다른 알고리즘에 비해 속도가 느릴 수 있음: 일부 특수한 문자열 패턴의 경우에는 다른 문자열 검색 알고리즘을 사용하는 것이 더욱 효율적일 수 있습니다. 예를 들어, 매우 긴 패턴을 가지는 경우에는 Boyer-Moore 알고리즘이 더욱 빠른 속도로 문자열 검색을 처리할 수 있습니다.
KMP 알고리즘을 사용하지 못하는 경우
KMP 알고리즘을 사용할 수 없는 경우가 있습니다.
-
첫째로, KMP 알고리즘은 주어진 문자열 내에서 부분 문자열을 검색하는 알고리즘이므로, 전체 문자열이 아닌 일부분만 검색하려는 경우에는 KMP 알고리즘을 사용할 수 없습니다.
-
둘째로, KMP 알고리즘은 메모리를 많이 사용하는 경향이 있습니다. 문자열 검색을 위해 이전에 매칭된 부분 문자열의 정보를 저장하는 배열을 사용하기 때문입니다. 따라서, 검색 대상 문자열이 매우 크고, 메모리 용량이 제한적인 환경에서는 KMP 알고리즘을 사용하기 어렵습니다.
-
셋째로, KMP 알고리즘은 문자열을 검색하는 과정에서 부분 문자열의 길이와 상관없이 일관된 시간 복잡도를 보장합니다. 하지만, 일부 특수한 문자열 패턴의 경우에는 다른 문자열 검색 알고리즘을 사용하는 것이 더욱 효율적일 수 있습니다. 예를 들어, 매우 긴 패턴을 가지는 경우에는 Boyer-Moore 알고리즘이 더욱 빠른 속도로 문자열 검색을 처리할 수 있습니다.
따라서, KMP 알고리즘이 항상 최적의 문자열 검색 알고리즘은 아니며, 검색 대상 문자열의 특징에 따라 다른 알고리즘을 선택해야 할 수도 있습니다.
오늘은 KMP 알고리즘에 대해 공부했는데 아직 실제로 사용해 보지 못해서인지 잘 이해가 안되는거같습니다
나중에 여유가 생겼을 때 KMP 알고리즘을 활용한 문제를 한번 풀어보면 좋을거 같습니다
오늘 푼 알고리즘 문제는 그래프 탐색 문제입니다
연결 요소의 개수
문제
방향 없는 그래프가 주어졌을 때, 연결 요소 (Connected Component)의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 정점의 개수 N과 간선의 개수 M이 주어진다. (1 ≤ N ≤ 1,000, 0 ≤ M ≤ N×(N-1)/2) 둘째 줄부터 M개의 줄에 간선의 양 끝점 u와 v가 주어진다. (1 ≤ u, v ≤ N, u ≠ v) 같은 간선은 한 번만 주어진다.
출력
첫째 줄에 연결 요소의 개수를 출력한다.
예제 입력 1
6 5
1 2
2 5
5 1
3 4
4 6
예제 출력 1
2
예제 입력 2
6 8
1 2
2 5
5 1
3 4
4 6
5 4
2 4
2 3
예제 출력 2
1
이문제는 간단히 연결된 노드들을 간선을 따라 dfs 혹은 bfs로 돌면서 방문한 노드들은 방문기록을 남기면 됩니다.
간선을 따라 연결된 노드들을 다 돌고 나서 dfs 나 bfs를 한번 빠져나올 때마다 카운트를 1씩 증가시켜서 총 몇번도는지만 체크하면 되는 문제입니다.
예) 위 문제에서 예제 입력 1과 같은 경우 1번 노드부터 dfs를 돈다고 했을 때 1,2,5 노드를 방문하게 되고 visited[1],visited[2],visited[5] 값들을 True로 바꿔주고 dfs를 빠져나오게 됩니다.
그렇게 빠져나왔을 때 count값을 +1 해주고 이제 이 후 2,5 노드 에서는 dfs를 시작할 일이 없습니다.
따라서 3노드 에서 dfs를 돈다고 했을 때 3,4,6 노드를 방문하게 되고 똑같이 visited[3],visited[4],visited[6] 값을 True로 바꿔주고 dfs를 빠져나온다. 똑같이 Count 값도 +1 하게 되어 2가 된다. 이제 visited[1] ~ visited[6] 까지 모두 True가 되었기 때문에 dfs를 돌 필요가 없으므로 정답은 2가 됩니다.
import sys
input = sys.stdin.readline
def dfs(start, depth):
# 현재 노드를 방문 처리
visited[start] = True
# 현재 노드와 연결된 다른 노드들에 대해서 재귀적으로 DFS 호출
for i in graph[start]:
if not visited[i]:
dfs(i, depth + 1)
n, m = map(int, input().split())
graph = [[] for _ in range(n+1)] # 각 노드에 대한 인접 리스트
for _ in range(m):
a, b = map(int, input().split())
graph[a].append(b) # a와 b 사이에 간선 추가
graph[b].append(a) # 양방향 그래프이므로 b와 a 사이에도 간선 추가
# 방문처리
visited = [False] * (n + 1)
count = 0 # 그래프 개수 저장
# 1 ~ n번 노드를 각각돌면서
for i in range(1, n + 1):
if not visited[i]: # 만약 i번째 노드를 방문하지 않는다면
if not graph[i]: # 만약 해당 정점이 연결된 그래프가 없다면
count += 1 # count에 + 1
visited[i] = True # 방문 처리
else: # 연결된 그래프가 있다면
dfs(i, 0) # dfs탐색
count += 1 # 개수를 + 1
print(count)내일은 보이어 무어에 관해 공부하고 그 뒤에는 오늘처럼 그래프 탐색 알고리즘 문제를 풀 거 같습니다
