4/22 보이어 무어(Boyer Moore)

보이어 무어(Boyer Moore)

보이어 무어 알고리즘은 문자열 검색을 빠르게 처리하는 데에 사용되는 알고리즘 중 하나입니다. 이 알고리즘은 일치하지 않는 문자열을 다시 검색하지 않고, 패턴 내의 특정 문자들을 기준으로 문자열 검색을 처리하는 방식으로 작동합니다

• 오른쪽에서 왼쪽으로 비교
• 대부분의 상용 소프트웨어에서 채택하고 있는 알고리즘
• 보이어-무어 알고리즘은 패턴에 오른쪽 끝에 문자가 불일치하고 이 문자가 패턴 내에 존재하지 않는 경우, 이동거리는 무려 패턴의 길이만큼
• 앞의 두 매칭 알고리즘의 공통점 텍스트 문자열의 문자를 적어도 한번씩 훑습니다.
• 보이어 무어 알고리즘은 텍스트 문자를 다 보지 않아도 됩니다
• 최악의 경우 수행시간 O(MN)
• 입력에 다라 다르지만 일반적으로 O(n) 보다 시간이 덜 소요됩니다

예시:

텍스트 STRING STARTING CONSISTING에 대하여 패턴 STING을 탐색하는 수행과정을 본다면

먼저 STING이라는 패턴에 대한 skip 배열을 구하여야 합니다.

• STING 일 때의 skip 배열

• 위와 같은 skip 배열의 숫자는 만약 텍스트가 일치하지 않을 경우 얼마만큼 건너뛰어야 하는지 표시한 것입니다.

• 오른쪽에서 왼쪽으로 탐색을 진행하기 대문에 먼저 N과 G를 비교해보면, 서로 다른 문자임을 알 수 있습니다
  위에 N 이란 단어는 skip 배열에서 1이란 숫자를 표시하고 있으므로 한 칸을 뛰도록 합니다.

• 1칸 이동 후
• 오른쪽부터 탐색해 봤을 때, G N I는 순서대로 일치하고 R과 T가 다른 것을 알 수 있습니다. 따라서 R은 skip 배열에서 정의하고 있지 않기 때문에 다른 모든 문자로 보고 5칸을 이동하도록 합니다.

• 5칸 이동 후
• 5칸 이동 후 탐색했을 때 R과 G 가 다르므로 또 R (다른 모든 문자) 값 5칸만큼 이동하도록 합니다

• 계속 이동해주도록 합니다.

• I 값은 skip 배열에서 2로 정의되어 있기 때문에 2칸을 이동해 주도록 합니다.

• T값은 3으로 정의되어 있으니 3만큼 이동하도록 합니다

• 탐색 완료

파이썬 코드

이제 보이어 무어 알고리즘을 파이썬으로 구현을 합니다

먼저 skip 배열을 만들어주는 initSkip() 함수를 구현합니다

def initSkip(p):
    NUM = 27  # 알파벳 수
    M = len(p) # 패턴의 길이
    skip = [M for i in range(NUM)] #skip 함수를 모두 M값으로 초기화
    for i in range(M):
        skip[ord(p[i]) - ord('A')] = M - i - 1 
    return skip # skip 배열 반환

print(initSkip("ATION")) # 임시로 ATION 이란 패턴을 입력

저는 여기서 skip[ord(p[i]) - ord('A')] = M - i - 1을 잘 이해하지 못해서 천천히 살펴봤습니다.

먼저, ord 함수는 특정 문자를 아스키 값으로 변환하는 함수입니다.
p [] 배열에는 A T I O N (문자열)이 순서대로 들어오게 됩니다.
여기서 ord 함수를 이용하여 아스키 값으로 변환하지 않는다면 문자에 정수 값을 대입하는 결과가 발생합니다
또 ord('A') 를 빼주는 이유는 skip 배열의 번호가 0번부터 시작되기 때문에 맞춰주기 위함입니다.

실행 결과

다음으로는 전체적인 보이어 무어 알고리즘 코드입니다.

def BM(p, t):
    M = len(p)
    N = len(t)
    skip = initSkip(p)

    i = M-1
    j = M-1

    while j >= 0:
        while t[i] != p[j]:
            k = skip[ord(t[i]) - ord('A')]
            if M - j > k:
                i = i + M - j
            else:
                i = i + k
            if i >= N:
                return N
            j = M - 1
        i = i-1
        j = j-1
    return i+1

print(BM("ATION","VISOINQUESTIONONIONCAPTIONGRADUATION"))

보이어 무어의 장단점

보이어 무어의 장점

• 일관된 시간 복잡도: 보이어 무어 알고리즘은 일관된 시간 복잡도를 보장합니다. 이러한 특징으로 인해, 검색 대상 문자열이 매우 긴 경우에도 빠른 검색 속도를 보여줍니다.
• 중복 검색 최소화: 보이어 무어 알고리즘은 패턴 내의 특정 문자들을 기준으로 문자열 검색을 처리하기 때문에, 중복 검색을 최소화할 수 있습니다. 따라서, 문자열 검색 시간을 단축할 수 있습니다.
  추가적인 메모리 사용 최소화: 보이어 무어 알고리즘은 다른 문자열 검색 알고리즘에 비해 메모리를 적게 사용합니다.
• 대부분의 상황에서 빠른 속도: 일반적으로 보이어 무어 알고리즘은 다른 문자열 검색 알고리즘에 비해 더 빠른 속도로 문자열 검색을 처리합니다.

보이어 무어의 단점

• 최악의 경우에도 선형 시간 복잡도를 보장하지 않음: 보이어 무어 알고리즘은 일반적으로 문자열 검색 시간을 매우 단축시키지만, 최악의 경우에는 선형 시간 복잡도를 보장하지 않습니다.
• 추가적인 전처리 시간이 필요: 보이어 무어 알고리즘은 패턴 내의 특정 문자들을 기준으로 문자열 검색을 처리하기 때문에, 전처리 시간이 필요합니다.
• 대소문자를 구분: 보이어 무어 알고리즘은 대소문자를 구분합니다. 따라서, 대소문자를 구분하지 않는 문자열 검색에는 사용할 수 없습니다.
• 패턴 내에 중복된 문자가 있을 경우 동작이 예상치 않게 될 수 있음: 패턴 내에 중복된 문자가 있는 경우, 보이어 무어 알고리즘의 동작이 예상치 않게 될 수 있습니다. 이러한 경우에는 다른 문자열 검색 알고리즘을 사용하는 것이 더욱 안전합니다.

어제 공부했던 KMP처럼 보이어 무어도 이론만 공부를 하니 잘 이해가 안되는거같습니다
나중에 보이어 무어도 KMP와 함께 활용 문제를 풀어보며 더 공부를 해야겠다고 느꼈습니다

오늘 푼 알고리즘 문제도 그래프 탐색 문제입니다

문제 링크

바이러스

문제
신종 바이러스인 웜 바이러스는 네트워크를 통해 전파된다. 한 컴퓨터가 웜 바이러스에 걸리면 그 컴퓨터와 네트워크 상에서 연결되어 있는 모든 컴퓨터는 웜 바이러스에 걸리게 된다.
예를 들어 7대의 컴퓨터가 <그림 1>과 같이 네트워크 상에서 연결되어 있다고 하자. 1번 컴퓨터가 웜 바이러스에 걸리면 웜 바이러스는 2번과 5번 컴퓨터를 거쳐 3번과 6번 컴퓨터까지 전파되어 2, 3, 5, 6 네 대의 컴퓨터는 웜 바이러스에 걸리게 된다. 하지만 4번과 7번 컴퓨터는 1번 컴퓨터와 네트워크상에서 연결되어 있지 않기 때문에 영향을 받지 않는다.

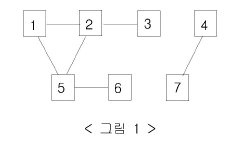
어느 날 1번 컴퓨터가 웜 바이러스에 걸렸다. 컴퓨터의 수와 네트워크 상에서 서로 연결되어 있는 정보가 주어질 때, 1번 컴퓨터를 통해 웜 바이러스에 걸리게 되는 컴퓨터의 수를 출력하는 프로그램을 작성하시오.

입력
첫째 줄에는 컴퓨터의 수가 주어진다. 컴퓨터의 수는 100 이하이고 각 컴퓨터에는 1번 부터 차례대로 번호가 매겨진다. 둘째 줄에는 네트워크 상에서 직접 연결되어 있는 컴퓨터 쌍의 수가 주어진다. 이어서 그 수만큼 한 줄에 한 쌍씩 네트워크 상에서 직접 연결되어 있는 컴퓨터의 번호 쌍이 주어진다.

출력
1번 컴퓨터가 웜 바이러스에 걸렸을 때, 1번 컴퓨터를 통해 웜 바이러스에 걸리게 되는 컴퓨터의 수를 첫째 줄에 출력한다.

예제 입력 1
7
6
1 2
2 3
1 5
5 2
5 6
4 7

예제 출력 1
4

DFS는 재귀 호출을 통해 구현할 수 있습니다. DFS 함수의 매개변수로 바이러스가 있는 컴퓨터의 번호를 받습니다. 위에서 만든 그래프를 보고, 해당 컴퓨터와 연결되어 있는 컴퓨터에 방문하지 않았다면 컴퓨터의 번호를 매개변수로 전달하면서 재귀호출을 합니다. 함수가 호출되는 수가 감염된 컴퓨터의 수입니다.

import sys
input = sys.stdin.readline

# 깊이 우선 탐색 함수 dfs 정의
def dfs(graph, root):
    # 현재 노드 방문 처리
    visited[root] = True
    # 현재 노드와 연결된 다른 노드들에 대해서 재귀적으로 DFS 호출
    for i in graph[root]:
        if visited[i] == False:
            dfs(graph, i)

# 정점의 개수와 간선의 개수 입력 받기
n = int(input())
m = int(input())

# 각 노드에 대한 인접 리스트 만들기
graph = [[] for _ in range(n+1)]
for _ in range(m):
    a, b = map(int, input().split())
    # 양방향 그래프이므로 a와 b 사이에 간선 추가
    graph[a].append(b)
    graph[b].append(a)

# 방문 여부를 저장할 리스트 만들기
visited = [False] * (n + 1)

# 1번 정점을 시작으로 DFS 탐색 실행
dfs(graph, 1)

# 1번 정점을 제외한 방문한 정점의 개수 계산
ans = visited.count(True) - 1

# 결과 출력
print(ans)