
Introduction
이번 포스팅에서는 Anomaly Detection의 첫 방법론 소개로 Model-based Methods의 Isolation Forest에 대해 살펴보도록 하겠습니다.
Isolation Forest란?
1. 개념 및 가정
Isolation Forest는 Unsupervised Anomaly Detection 중 하나로 현재 갖고 있는 데이터 중 이상치를 탐지할 때 주로 사용됩니다. 이름에서 볼 수 있듯이 tree 기반으로 구현되는데, 랜덤으로 데이터를 split하여 모든 관측치를 고립시키며 구현됩니다.
특히, 변수가 많은 데이터에서도 효율적으로 작동할 수 있는 장점이 있습니다.
The term isolation means ‘separating an instance from the rest of the instances’.
- Isolation Forest original paper
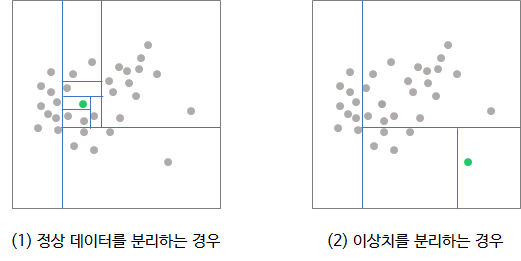
Isolation Forest의 컨셉은 "각 관측치를 고립(=분리)시키기는 것은 이상치가 정상 데이터보다 쉽다."입니다.
위의 예제는 다음과 같이 해석됩니다.
(1) 정상 데이터를 분리하는 경우, 약 7번의 split 필요
(2) 이상치를 분리하는 경우, 약 3번의 split 필요
2. 학습 방법
- 정상 데이터는 tree의 terminal node와 근접하며, 경로길이가 큼
- 이상치는 tree의 root node와 근접하며, 경로길이가 작음
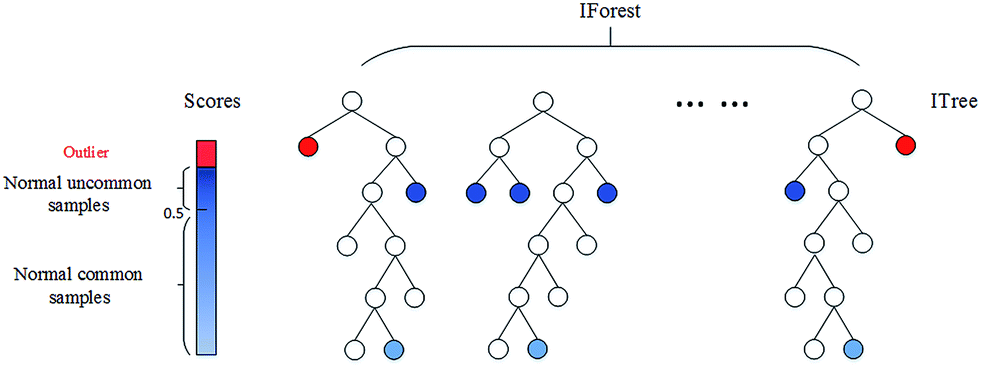
랜덤포레스트가 의사결정나무를 여러번 반복하여 앙상블 하듯이, Isolation Forest는 iTree를 여러번 반복하여 앙상블 합니다.
iTree
- Sub-sampling : 비복원 추출로 데이터 중 일부를 샘플링
- 변수 선택 : 데이터 의 변수 중 를 랜덤 선택
- split point 설정 : 변수 의 범위(max~min) 중 uniform하게 split point를 선택
- 1~3번 과정을 모든 관측치가 split 되거나, 임의의 split 횟수까지 반복(=재귀 나무)하며, 경로길이를 모두 저장
Isolation Forest
5. 1~4번 과정(iTree)을 여러번 반복
3. Scoring
- : 해당 관측치의 경로길이
- : 모든 iTree에서 해당 관측치에 대한 평균 경로길이
- : 를 nomalise하기 위한 값으로, 의 평균 경로 길이. (iTree는 Binary Search Tree와 동일한 구조이기 때문에, 값을 쉽게 구한다고 함.)
에 따른 Score 값을 보면, 아래와 같습니다.
- 관측치 x가 전체 경로길이의 평균과 유사(= 정상 데이터) : ,
- 관측치 x가 이상치 : ,
- 관측치 x의 최대 경로길이 : ,
즉, Score는 0 ~ 1 사이에 분포되며, 1에 가까울 수록 이상치일 가능성이 크고 0.5 이하이면 정상데이터로 판단할 수 있습니다.
Summing up
- Unsupervised Anomaly Detection : Isolation Forest는 데이터에서 이상치를 탐지하기 위한 방법론입니다.
- Random Forest와 비슷하게 작동하며, 여러개의 iTree로 구성됩니다.
- 고차원 데이터에서도 작동할 수 있는 강점이 있습니다.
Reference
- Liu, F. T., Ting, K. M., & Zhou, Z. H. (2008, December). Isolation forest. In 2008 Eighth IEEE International Conference on Data Mining (pp. 413-422). IEEE.
- 김동화님 블로그(DSBA 연구실)
- 도도댕님 블로그
- Eryk Lewinson 블로그
