[DevCourse] 11-3 선형 회귀

선형 모델의 개념

• 과자(1,500원)와 우유(1,200원)를 사기위해 마트에서 장을 본다고 가정하자.

• total cost = n(과자) 1500 + n(우유) 1200

  • 조건(과자의 가격과 우유의 가격은 서로 독립)

• 이처럼, 독립 변수 (n(과자, 우유))가 파라미터 (가격) 값 만큼 일정한 비율로 종속 변수 (total cost)에 영향을 미치는 관계가 선형 관계이다.

• 종속변수 y에 대해 파라미터들이 선형 결합을 이루고, 이것으로 종속 변수의 값을 표현 할 수 있는 경우, 이를 선형 모델이라고 한다.

  • y = w1x1 + w2x2 + ... + wnxn (xi : feature, wi : parameter)
  • 선형 모델을 그래프로 표현한다면 직선(2D), 평면(3D), 혹은 Hyper-plane(4D 이상)이라고 한다

• 데이터가 작을 때 좋은 모델이다

• 선형 vs 비선형

• 선형 모델에서는 기본적으로 "독립 변수"들은 서로 상관관계가 없는경우를 가정한다.

• 다중 공선성 문제 (Multicollinearity Problem) : 독립 변수 사이에 높은 상관관계가 있어 모델의 성능이 저하되는 문제

  • 해당 문제가 발생하는 경우 다른 모델을 사용하는 것이 좋다.

• 결과적으로 선형 회귀 모델을 사용하는 것은 :: 입력 데이터의 독립성을 가정하고 데이터 특징에 대한 선형 결합으로 회귀 문제를 풀겠다는 의미이다.

  • w0(y 절편)는 목표값의 평균으로 설정한다.

  

• 비용 함수(J(w)) = MSE (Mean Squared Error) : 예측값과 실제값의 오차(Error)를 제곱(Square)하여 평균(Mean)을 구한다

  • 선형 모델에서는 min(J(w))인 w(parameter)를 찾아내야함! -> 최적화

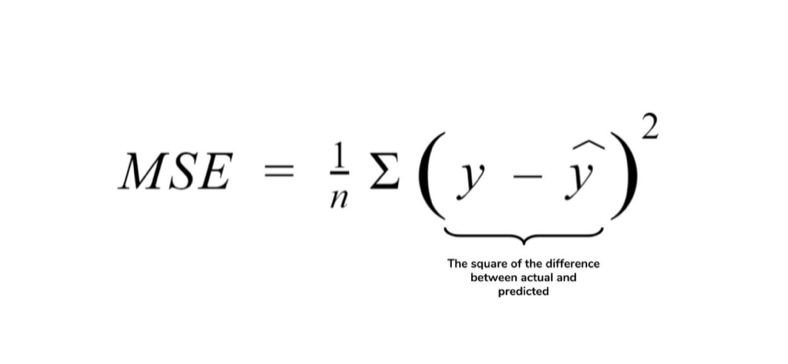
선형 모델의 최적화 : 정규 방정식 (OLS)

• 식의 기울기가 0이 되는 위치를 찾기, 즉 J(w)의 도함수를 구하고 그것이 0이 되는 w를 구해야 한다. 결과적으로 w의 유일한 해를 직접 구할 수 있다

• 시간 복잡도가 O(p^3)이다 (p : feature의 개수)
  • 따라서, feature의 수가 적을 때 사용하기 좋은 방법이다.

선형 모델의 최적화 : 경사 하강법

• 임의로 설정한 초기 w 값을 기준으로 J(w)의 기울기를 계산하여 기울기가 0에 가까워지는 방향으로 w값을 점진적으로 수정

  • 적절한 학습 속도(learning rate, w의 변화값)에 대한 탐구가 필요
    • learning rate가 너무 작다면 최적화 소요 시간이 늘어난다
    • learning rate가 너무 크다면 최적값 도달 가능성이 적어진다

  

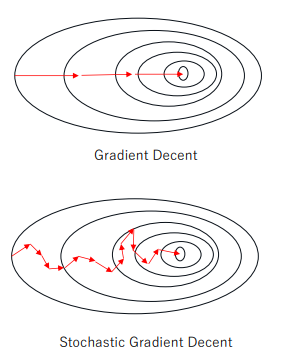
• 모든 test data에 대해 iterative하게 진행되기 때문에 확률적 경사 하강법 (Stochastic Gradient Decent)를 더 많이 사용한다.

• 확률적 경사 하강법 (Stochastic Gradient Decent) : 전체 데이터 중 임의로 일부 데이터를 샘플링하여 그것을 대상으로 경사 하강법을 진행한다. 즉, 작은 데이터로 수정 이동을 반복하여 빠른 수렴이 가능하다.

  • 데이터의 수가 많거나 (n >> ), feature이 많은 경우 (p >> ) 사용하기 용이하다.

  

다중공선성 (multicollinearity)

• feature들 사이에 상관 관계가 존재할 때 발생하는 문제 상황 -> ML 모델이 작은 데이터의 변화에도 민감하게 반응하여 안정성과 해석력을 저하시킨다

• 특히 정규 방정식으로 해를 구하는 상황에서 T(X)X의 역행렬이 존재하지 않을 수 있어 치명적이다.

• 회피 방법 (해결 방법 XXX) = SVD-OLS : 특이값 분해를 사용하여 선형 회귀 모델의 해를 구하는 방법. 정확한 해를 구하는 방법은 아니다.

• 시간 복잡도 : O(np^2)

  • 일반적으로 n >> p 이므로 SVD-OLS의 시간복잡도가 OLS보다 크다

• 다중공선성이 존재하지 않는 경우 SVD-OLS의 결과값과 OLS의 결과값은 (거의) 동일하다.

• scikit-learn 패키지에는 성능이 더 좋은 TSVD-OLS가 구현되어 있다

규제를 사용하는 선형 모델

• ML 모델에서 overfitting 문제가 발생 할 경우 w의 값이 매우 커진다. 그래서 w의 값이 너무 커지지 않도록 규제(regulation)을 가해 overfitting 문제를 회피하는 모델

  • 규제 : 비용함수에 새로운 값을 추가
    

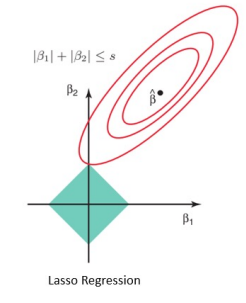
• 라쏘 회귀 (Lasso Regression)

  • L1 규제를 사용. 해당 규정은 일부 파라미터의 값을 0으로 설정할 수 있음.
  • 변수가 많고, 일부 변수가 중요한 역할을 도맡아 하는 경우 모델을 단순화해준다는 장점이 있다

  

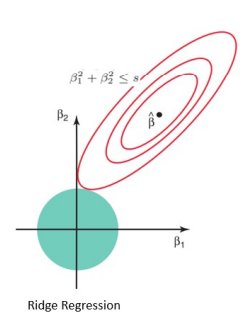
• 릿지 회귀 (Ridge Regression)
  • L2 규제를 사용. 해당 규정은 w값을 적당히 작게 만들어준다 (0이 되지는 않음)
  • 모든 feature가 출력 결과에 적당하게 영향을 미치는 경우에 유용하다

로지스틱 회귀 (Logistic Regression)

• 기본적으로 이진 분류 문제를 해결하기 위한 알고리즘. 각 후보 클라스의 확률을 예측(확률 추정)하는 방식으로 문제를 해결한다

• 일반적으로 확률 값이 50% 이상(양성, positive)이면 해당 클래스에 속한다고 예측한다. (<-> 음성)

• Logistic Regression의 경우도 선형 모델의 조건(독립 변수간 독립성)을 가정한다

• J(w) = 로그 손실(log loss)

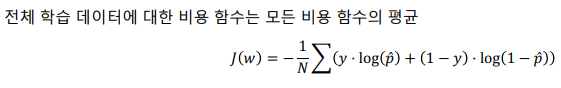
• Logistic Regression의 경우는 SGD를 사용하여 min(J(w))를 사용하여 최적값을 찾아야한다 (OLS와 같은 방정식은 존재하지 않음)

Softmax Regression

• multi-label classification이다 ex) 뉴스 기사의 카테고리를 예측한다

의료비 개인 데이터셋을 통한 선형 회귀 실습

• 데이터셋 (Medical Cost Personal Datasets)

• 목적 : 주어진 건강 및 인구통계학적 정보(독립 변수)를 바탕으로 개인의 연간 의료 보험료(종속 변수)를 예측한다

• 진행 순서 ([Part4, Chap10] 선형 회귀 실습.ipynb)

  • 기본적인 EDA 진행

    • 총 1338개의 개별 데이터
    • 7개의 col
    • 결측치 없음
    • 시각화로 데이터의 특성 파악

  • 데이터 전처리

    • 범주형 변수(성별, 흡연 유무, 지역)는 one-hot encoding 방식을 사용하여 인코딩
    • 학습 / 평가 데이터로 분리
    • 독립 변수와 종속 변수를 분리
    • scaling(수치형 데이터의 값 범위를 비슷하게 맞춰주기) 진행
      • 분포의 특징에 맞는 scaler를 사용하는 것이 좋다
      • StandardScaler : 데이터를 정규분포 형태로 변환
      • MinMaxScaler : (0 ~ 1) 사이의 값으로 조정. 이상치가 큰 영향을 미치는 경우 유용

  • 간단한 선형 회귀 모델을 만들고 결과 확인
    

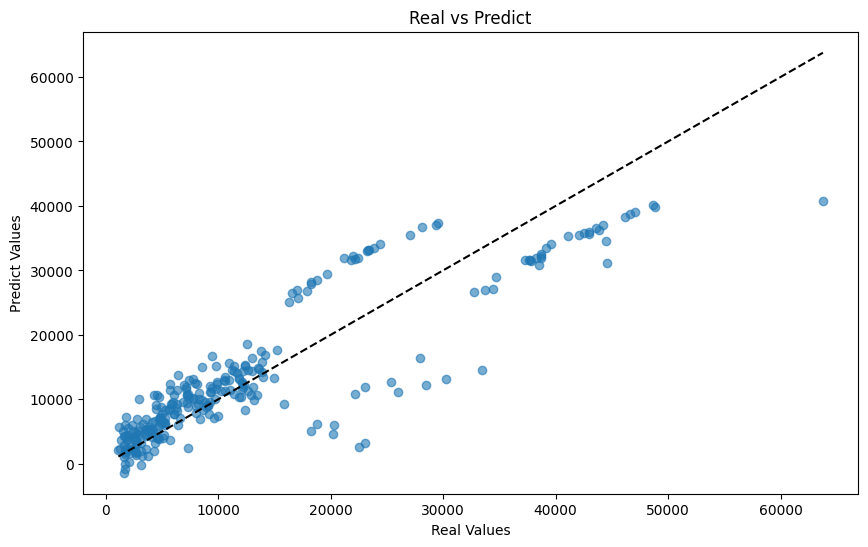
  • feature 레벨로 영향력 확인
    

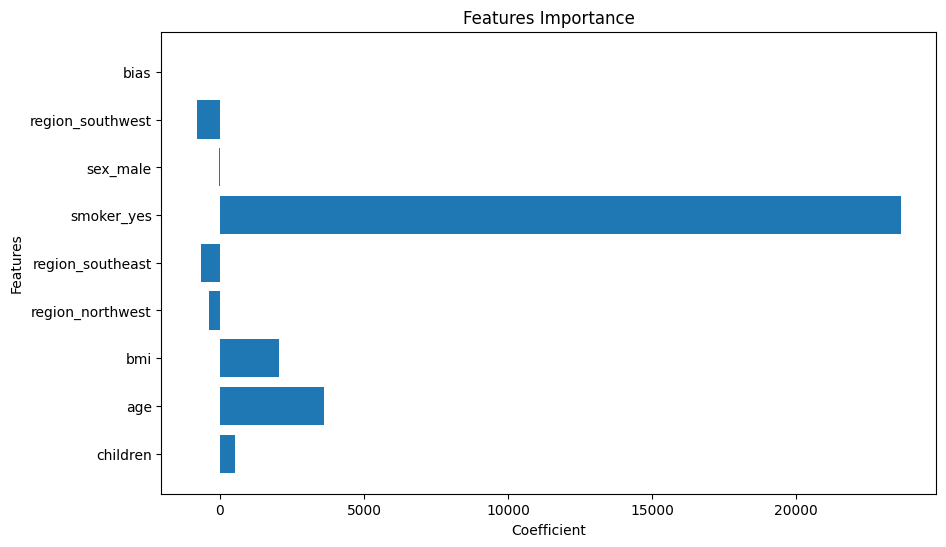
  • 잔차분석 진행
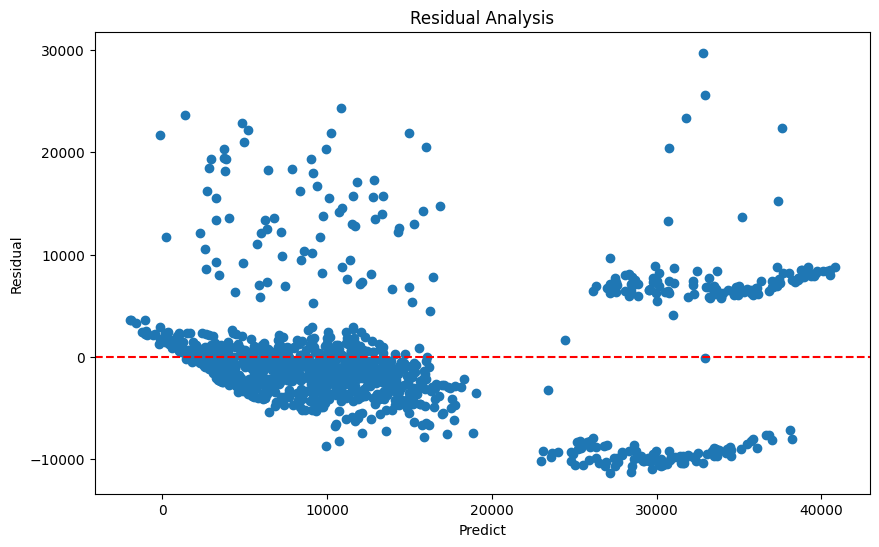