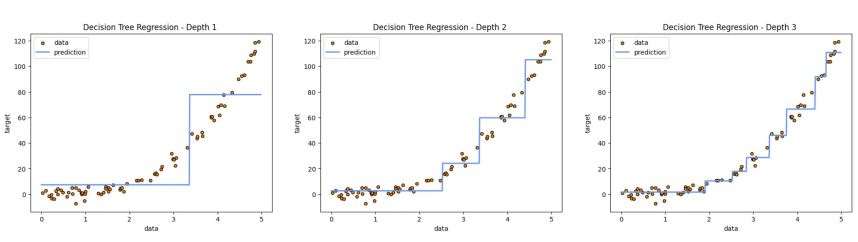
잘 분류한다는 것

- 빨간 선, 파란 선 모두 삼각형과 원을 정확하게 분류하였다
-
파란 선의 경우 각 클래스의 데이터 샘플로부터 가장 멀리 위치해있다 -> 일반화 성능이 빨간 선보다 좋다
-
샘플로부터 분류 선까지의 거리를 마진(Margin)이라고 하며, 마진을 구성하는 데이터 샘플을 서포트 벡터(Support Vector)라고 한다.
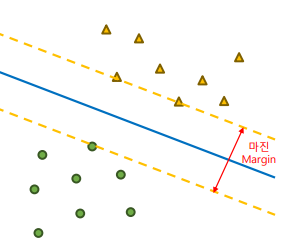
선형 SVM의 목적
-
SVM은 마진을 최대화하며, 두 데이터를 분류하는 직선/초평면을 찾는 것이 목적이다. (= 최대 마진 초평면을 찾는 것)
-
최대 마진 초평면(maximal margin hyperplane)의 방정식은 아래와 같다

- 이때, 마진은 아래와 같이 계산 가능하다

하드 마진 SVM (선형)
- 어떠한 오분류도 허용하지 않고 최대 마진 초평면을 구성하는 방식
소프트 마진 SVM (선형)
-
완벽한 선형 분리가 불가능한 경우 어느 정도의 오분류를 허용하며 일반화 성능을 올리는 방식
-
슬랙 변수 (Slack variable) : 소프트 마진 SVM에서 사용하는 개념으로, 하나의 데이터 포인트에 대해 해당 데이터 포인트가 마진을 얼마나 위반하는지를 수치적으로 나타내는 지표
-
1) 마진 경계를 위반하지 않은 데이터 : ξ = 0
-
2) 마진 경계를 위반, 결정 경계를 위반하지 않은 데이터 : 0 < ξ <= 1
-
3) 결정 경계를 위반한 데이터 : 1 < ξ
- 3의 경우 올바르지 못한 분류로 간주한다
-
-
하드 마진 SVM의 최적화 과정에 오차에 대한 패널티를 추가한 일반화 식을 사용한다
- 1) 마진의 크기를 최대화
- 2) 마진 위반(패널티)를 최소화
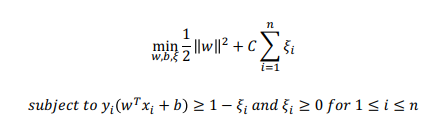
- C : 일반화를 위한 하이퍼파라미터. 오차에 대한 패널티의 크기를 결정.
- 작은 C값을 사용 : 오류를 많이 허용하며, 모델이 유연해진다. Underfitting 문제가 발생 할 수 있다.
- 큰 C 값을 사용 : 모델은 더 제약된 형태로 변하게 된다. 즉, 테스트 데이터에 대해 overfitting 문제가 발생한다.
- 보통 교차 검정 (Cross-Validation)을 통해 최적의 C값을 찾아낸다
비선형 SVM
-
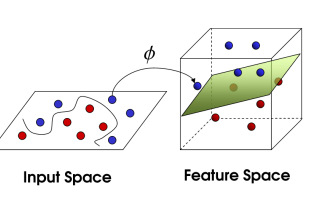
데이터의 특성이나 복잡도에 따라 데이터를 선형으로 분류할 수 없는 경우가 있다
-
위와 같은 경우, Mapping function을 사용하여 데이터의 차원을 늘려 초평면으로 분류해 볼 수 있다
-
하지만, 데이터의 차원을 늘리면 계산량, 복잡성이 크게 늘어난다. 이를 해결하기 위해 커널 트릭(Kernel Trick)을 사용함
-
커널 트릭(Kernel Trick) : 커널 함수를 사용하여 고차원의 내적 연산과 같은 결과를 보여주는 방법
- 다항 커널 (Polynomial Kernel) : 다양한 차수 설정으로 여러 식을 근사할 수 있지만 overfitting의 위험이 있음
- 가우시안 커널 / RBF 커널 (Gaussian Kernel) : 유연성이 높으며, 다양한 데이터에 적용 가능한 범용성이 높은 함수
- 시그모이드 커널 (Sigmoid Kernel) : 이진 분류에 최적화된 함수 (잘 안쓴다)
-
최적화함수는 소프트 마진 SVM과 비슷한 구조를 가지고 있다

SVR (Support Vector Regression)
-
SVM을 회귀 문제로 확장.
-
주어진 데이터에서 가능한 많은 데이터 포인트를 포함하는 마진 구역을 설정하고, 해당 마진 구역 안에서 회귀 직선/초평면을 찾는것이 목표이다.
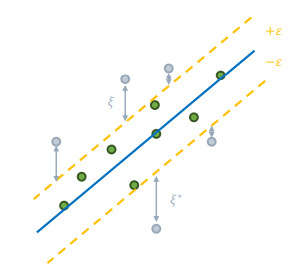
-
주어진 데이터에서 가능한 많은 데이터를 포함하는 마진 구역을 설정한다. 마진 구역의 안쪽에 해당하는 데이터(초록색으로 표시)만 사용하여 회귀 직선/초평면을 구성하고, 나머지 데이터들(회색으로 표시)는 outlier로 취급하여 drop한다.
-
최적화 함수는 아래와 같다

Decision Tree
- 기준을 설정하여 데이터를 분류하는 방법론
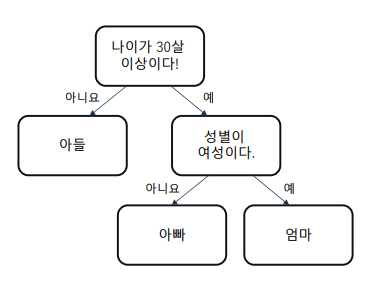
- pros
- 해석이 편리하다 => root node에 가까운 결정 기준일수록 영향이 큰 feature
- 평균적인 성능
- 스케일링에 둔감하다
- cons
- 축이 수직인 방향으로 데이터가 분할된다 => 일반화에 어려움이 있다
- 주성분 분석을 통한 데이터 회전을 진행하는 경우도 있다
- 노이즈에 굉장히 민감하다
- Depth가 깊어질수록 Overfitting의 위험이 커진다
- 축이 수직인 방향으로 데이터가 분할된다 => 일반화에 어려움이 있다
Decision Tree 분류 결정 기준
-
결정 기준 : 데이터를 분할하는 기준을 결정하는데 사용하는 방법론이다
-
엔트로피 : 어떤 상황이나 현상이 품고 있는 불확실성
- 엔트로피가 크다 == 불확실성이 크다(데이터가 고르게 분포) == 정보량이 적다
-
각 노드에 포함되는 데이터의 순도(분포)에 따라 엔트로피를 계산할 수 있다.
- 노드 안에 서로 다른 클래스의 데이터가 많이 섞여 있는 경우 순도가 낮다
- 같은 클래스의 데이터가 모여 있다면 순도가 높다
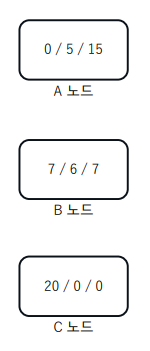
-
ex) 위 그림에서 각 노드의 엔트로피의 크기는 C < A < B이다.
-
정보 이득 (information gain) : 부모 노드와 자식 노드들의 엔트로피를 계산하여 엔트로피가 낮아지는 방향으로 결정 경계를 선정하는 것을 의미한다
- 트리를 내려감에 따라 불확실성은 작아지고, 정보는 많아져야 한다
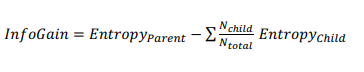
- 지니 불순도 (Gini Impurity) : 데이터 안에 존재하는 클래스 분포의 불균형을 평가하는 방법. 0 (순도가 높음) 이상, 1 (순도가 낮음) 미만의 값을 가진다.
-
엔트로피 VS 지니 불순도, 어떤 결정 기준을 사용해야 할까?
-
일반적으로 지니 불순도의 계산이 더 빠르다
-
일반적으로 엔트로피가 조금 더 균형 잡힌 트리를 만드는 경향이 있다
-
당연히 가장 좋은 것은 두 방식 모두 사용해보고 선택하는 것이다
-
Decision Tree 회귀
- Depth를 늘려가며 MSE의 평균을 최소화하는 노드를 찾아가는 방식으로 Tree가 만들어진다