[강화학습] Deep Reinforcement Learning

Vaughan·2023년 1월 5일

강화학습

목록 보기

2/6

1. Deep Reinforcement Learning

1.1 Needs for DRL

기본적인 강화학습 방법들은 Agent가 반복해서 시뮬레이션하면서 Agent가 겪는 경험들을 이용하여 action을 선택할 때 참조하는 일종의 look-up table을 갱신하는 방법이었다. 즉, 경험;heuristic을 통해 데이터베이스를 쌓아가면서 나에게 유리한 action과 그렇지 않은 action을 구분해나가는 방법이다.

*look-up table : 특정한 state에 연관된 action과 reward를 기록한 table

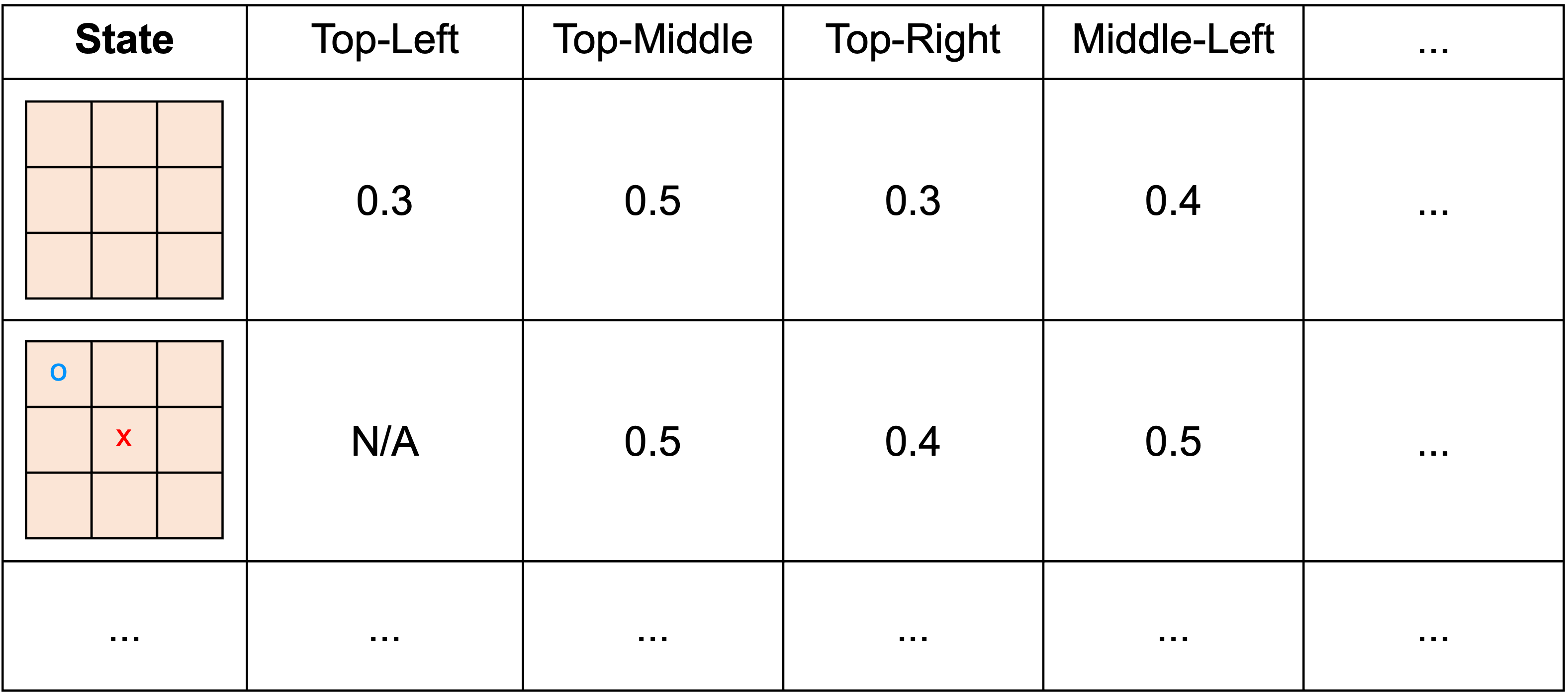
그러나 더이상 모든 state와 그때의 가능한 모든 action을 표기할 수 없을정도로 큰 state space, action space를 갖는 환경이라면, look-up table의 형식으로 표현하는것이 불가능하다.

Deep Reinforcement Learning은 신경망을 이용하여 학습하면서, 주어진 state에서 중요한 feature만을 뽑아내어 state를 자동으로 분석한다. 신경망 모델에서 사용되는 parameter는 가능한 모든 state의 조합을 저장하는데 필요한 항목의 개수보다 훨씬 적다!

예를 들어, Atari 2600 게임을 플레이하는 강화학습 agent를 학습하는데 사용했던 구글 딥마인드의 DQN의 파라미터의 개수는 $1792$ 개 뿐이지만 실제로 비디오 게임 화면( $84\times 84$ gray scale image)의 고유한 표현상태는 $256^{28228}$ 개 였다.

DRL의 발전과 함께 강화학습도 많은 발전을 이루었으며, 실제 세계의 대부분의 문제는 매우 복잡한 state-action space를 가지기 때문에 실제 세계의 문제에 적용하기 위해서는 대부분 DRL을 사용한다.

1.2 Category of (Deep)RL

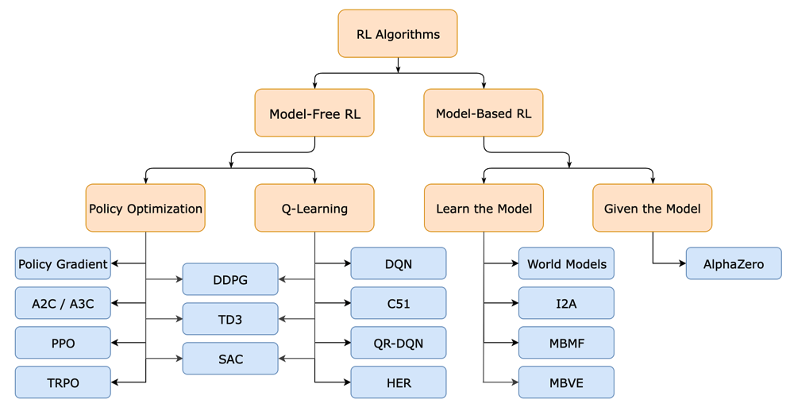
강화학습 알고리즘을 구분하는 기준은 크게 2가지로 나뉜다.

모델이 존재하는가?
- Model-Free RL
  - 모델이 존재하지 않는 RL
  - 실제 문제에서는 Environment를 정확히 묘사할 수 있는 모델을 구하는것이 매우 어렵다.
- Model-Based RL
  - 모델이 존재하는 RL
  - Environment를 정확히 표현할 수 있는 모델이 존재한다면, env와 실제로 상호작용하지 않고도 모델을 이용하여 Planning을 할 수 있다. → 즉, 실제로 Action을 하기전에 미리 simulate해보고 최적의 action을 선택할 수 있다.
  - 모델이 주어진 경우와, 모델을 스스로 학습하는 2가지 범주로 분류할 수 있다.
  - 대표적인 model-based RL이 바로 AlphaZero이다.
Value function / Policy 중에서 무엇을 최적화하는가?

Value function을 학습한다면, 각각의 state에서 최적의 value를 갖는 Action만을 선택하면 Optimal Policy를 구할 수 있다. 반면에 Policy를 학습한다면, value function은 Policy를 얻기 위하여 중간 계산과정일 뿐이기 때문에 Optimal Policy를 구할 수 있다.
- Policy-based method (Policy Optimization)
- Value-based method (Q-Learning)
(완벽하게 2가지 범주로 구분되는 것은 아니고, 2가지를 모두 함께 학습하는 Actor-Critic 등의 방법들도 존재한다.)

2. DQN

2.1 Q-Learning

Q-Learning은 간단하게 설명하자면, 각각의 state에서 선택한 action에 따른 reward값을 이용하여 Q(=value function)값을 계속해서 갱신해나가는 과정이다. (using Bellman Optimal Equation)

💡 현재의 추측 value 값을, 바로 그 다음 time-step에서의 추측 value값을 이용하여 갱신하자

Q-Learning의 분류

Temporal-Difference; TD episode가 끝날 때까지 기다리지 않고, 그 다음 time-step에서 즉각적으로 얻은 return과 그때의 value를 이용하여 갱신을 수행한다. (↔ episode가 끝날 때 까지 기다리는 방법이 MC)
Model-Free RL
Value based method (보통 $\epsilon$ -greedy와 같은 policy를 사용하여 action을 선택한다.)
off-policy

*off-policy와 on-policy?

off-policy는 실제로 environment와 상호작용하면서 경험을 쌓는 Agent와 실제로 내가 갱신하고자하는 Agent가 다른 경우를 뜻한다.

on-policy : target policy = behavior policy
off-policy : target policy ≠ behavior policy

예를 들어, 실제로 게임을 하면서 경험을 쌓아 티어가 올라가는 경우는 off-policy를 사용하는 것이고 게임을 계속 플레이하는 사람의 뒤에서 그 사람이 플레이 하는 것을 보고 학습하는 경우는 on-policy를 사용하는 것이다.

off-policy를 사용하는데에는 다음과 같은 이유가 존재한다.

사람이나 다른 RL method를 이용하여 학습된 Agent를 이용할 수 있다.
behavior policy를 따르는 agent가 수행한 결과를 보고, 좋지 못한 결과를 만드는 action의 경우에는 수정할 수 있다.

ex) 바둑에서 잘못된 곳에 둬서 승률이 급격하게 떨어지는 것을 확인했다면, target policy를 수정할 수 있다.

2.2 Q-update : in Formal

아이디어 : Bellman Optimal Equation for $q_{*}$

벨만 최적 방정식에 따라, $R_{t+1} + \gamma\max_a q_*(S_{t+1}, a)$ 의 기댓값이 $q_*(S_t, A_t)$ 이다. 즉, 여러번의 반복을 통해 바로 그 다음 time-step에서의 값을 모을 수록 점점 value function의 값을 업데이트 할 수 있을 것이다.

q_*(S_t, A_t) = \mathbb E_{S_{t+1}}[R_{t+1} + \gamma\max_{a}q(S_{t+1}, a)]

Notation
- $Q$ : value-function
  → state와 그때 수행한 action이 주어지면 value를 평가하여 반환하는 함수
- $S_t$ : time-step $t$ 에서 state
- $A_t$ : time-step $t$ 에서 수행한 ation
각 term의 의미
- $\alpha$ : 갱신할 때, 새로운 값을 기존의 value-function값에 비하여 어느정도로 고려할 것인가?
- $R_{t+1} + \gamma \max_{a} Q(S_{t+1}, a )$ : TD target $\epsilon$ -greedy 등의 policy를 이용하여 transition한 뒤, 다음 time-step에서 value를 최대로 하는 action을 선택했을 때의 value와 return의 합 즉, Q-learning은 off-policy를 이용하기 때문에 transition은 behavior policy를 따라서 수행하고 이동한 미래의 state에서 value를 계산할 때는 target policy를 이용한다. ⇒ Target과 기존 값 $Q(S_t, A_t)$ 의 차이를 이용하여 Q-update를 수행한다.

Q(S_t, A_t) \leftarrow Q(S_t,A_t) + \alpha(R_{t+1} + \gamma \max_{a} Q(S_{t+1}, a )- Q(S_t, A_t)))

위와 같은 Q-update과정을 반복해서 수행하여 최종적으로 얻은 Optimal action value function은 다음의 수식으로 표현할 수 있다.

Q_*(S_t, A_t) = \mathbb E_{S_{t+1}} [R_{t+1} + \gamma \max_{a} Q_*(S_{t+1}, a)]

2.3 DQN

DQN은 Q-Learning에서 value function을 Table형태가 아닌 “신경망”으로 표현하기 때문에, $Q$ 는 신경망의 parameter $\theta$ 에 영향을 받게 된다. 따라서 DQN에서는 value function term을 $Q_\theta$ 로 표현한다.

DQN으로 표현한 Q-Learning의 수식

Loss function 실제 정답을 $R_t + \gamma \max_{a_{t+1}}Q_{\theta}(s_{t+1}, a_{t+1})$ 라고 보고, 현재 value function값과의 차이의 제곱으로 loss를 표현한다. $L(\theta) = \mathbb E[(R_{t+1} + \gamma \max_{a}Q_{\theta}(S_{t+1}, a) - Q_{\theta}(S_t, A_t))^2]$
parameter update $\theta' = \theta + \alpha\left(R_{t+1} + \gamma \max_{a}Q_{\theta}(S_{t+1}, a) - Q_{\theta}(S_t, A_t)\right)\nabla_\theta Q_\theta(S_t, A_t)$

DQN의 성능향상을 위한 방법

Replay Buffer
- 이미 한번 겪었던 경험을 재사용함으로서 이전에 있었던 실수를 줄이고 더 나은 방향으로 학습하게하기 위하여 도입한 개념
- 여러개의 경험들을 저장해두었다가 샘플링하여 학습하면서, 여러번 재사용될 수 있다.
- 샘플링 되어 뽑히는 경험들은 실제 episode의 연속된 state와 달리 state간의 상관성이 떨어지기 때문에 더 효율적으로 학습할 수 있다.
target Network
- 학습 대상이 되는 Q-net과 정답을 계산할 때 사용되는 network 2가지를 사용하여 각 network에 사용되는 parmeter를 달리하는 방법
- 정답을 계산할 때 사용하는 네트워크가 자주 갱신되는 것은 학습의 안정성을 떨어트리기 때문에, 매우 긴 일정 주기마다 한번씩 정답 네트워크의 parameter를 갱신해준다.

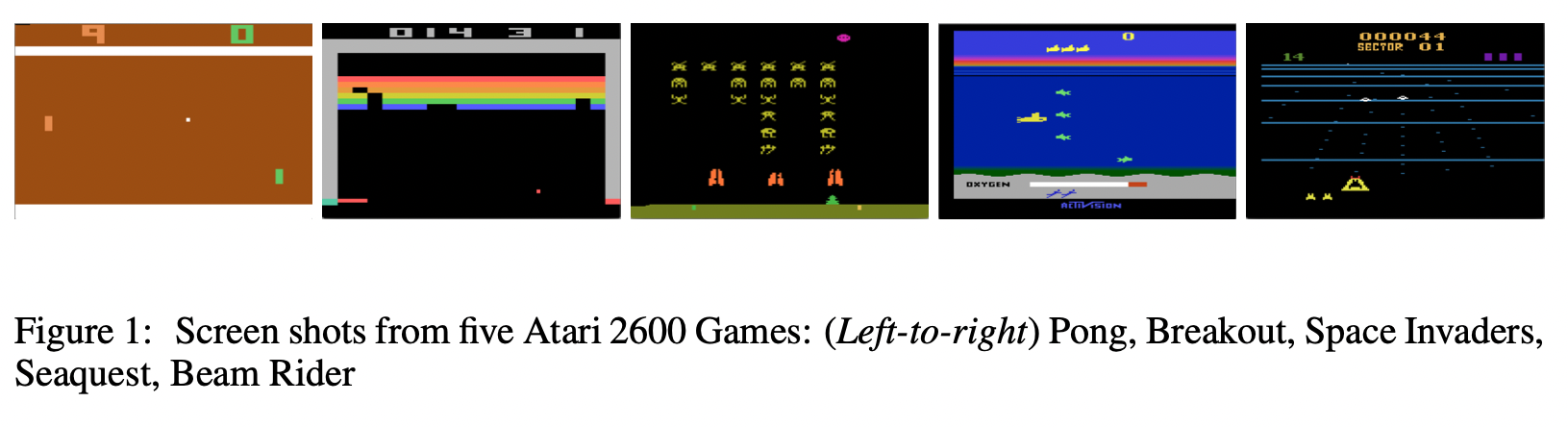
2.4 Playing Atari with Deep Reinforcement Learning

“Playing Atari with Deep Reinforcement Learning” 은 처음으로 Neural Net과 Reinforcement Learning을 결합하여 유의미한 성과를 보인 논문이다.

Atari 2600 Games

Agent가 플레이하는 게임 : Atari 2600 games ⇒ 각각의 게임에 대해 학습한다면 여러 게임을 플레이할 수 있는 강화학습의 “알고리즘” 개발
게임 화면 : $210 \times 160$ (pixel) RGB video (60 Hz)

DQN Network 구조

게임 화면 “이미지”를 입력받기 때문에 CNN을 사용한다.

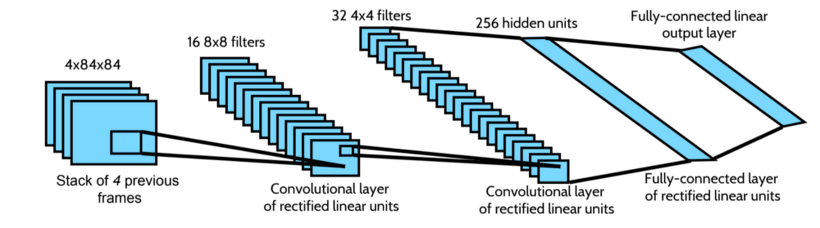
DQN Algorithm

notation
- reward $r$ : game score
- $s_1 = \{x_1\}$ : 한 episode의 sequence를 초기화 → observation과 action의 sequence
- $x$ : observation → 게임 화면
- $\phi$ : image preprocessing
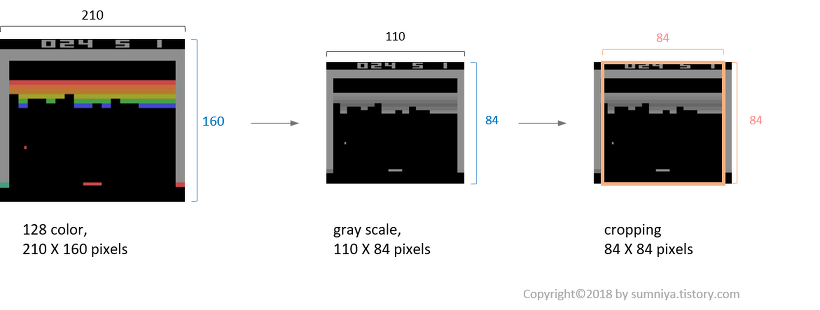
반복문
- for episode : 각각의 episode별로 반복하며 $M$ 번 수행
- for t : episode의 sequence time-step별로 반복

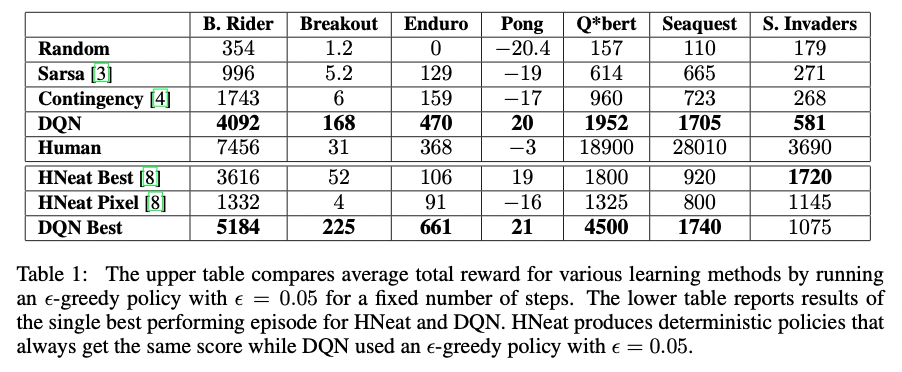
Reward 비교

다른 방법을 이용하여 학습한 모델들과 비교했을 때 훨씬 띄어난 성능을 보였으며, 몇몇 게임의 경우에는 심지어 사람이 play한 것보다도 좋은 성능을 보이는 것을 확인할 수 있다.

3. Policy Gradient Method

3.1 Concept of Policy Gradient

Action을 선택하기 위한 Policy를 참조할 때, Value function없이도 action을 선택할 수 있는 파라미터 기반의 policy를 학습하는 방법이다.

$\theta \in \mathbb R^d$ 로 표현되는 policy parameter vector를 이용하여 policy를 정의하고, parameter에 대한 value를 나타내는 $J(\theta)$ 의 gradient를 이용하여 policy의 parameter를 학습할 것이다.

policy를 나타내는 신경망의 구조
- input : state
- output : 그 state에 대한 각각의 action의 확률

Needs for Policy Gradient method

value based Agent는 Optimal value function $Q_*$ 를 구하면, action을 선택할 때는 항상 value가 최대가 되게 하는 action만을 deterministic하게 선택한다.

그러나 policy는 $\pi(s,a) = \mathbb P[a|s]$ 처럼 “확률”로서 정의되기 때문에 policy based Agent는 다음 action이 non-deterministic한 유연한 선택을 할 수 있게 해준다.

Example

예를 들어, 가위바위보 게임에서 처음으로 낼 action을 고른다고 가정하자.

value based Agent에서 Optimal value function의 값이 $Q_*(s_0, 보) = 0.1, Q_*(s_0, 주먹) = 0.8, Q_*(s_0, 가위) = 0.5$ 이라면 Agent는 $\max_a Q_*(s_0, a)$ 을 따라 항상 “보”만을 선택하게 된다.

그러나 policy based Agent가 갖는 policy가 각각의 action에 대해 $1/3$ 이라면, 각각의 action을 선택할 확률이 $1/3$ 이 되어 $s_0$ 이 주어질 때마다 다른 action을 선택할 수 있다.

3.2 Policy Optimization : in formal

Policy Optimization을 위한 아이디어

loss의 정의
Policy Neural Net을 학습시키기 위해서는 Loss를 정의해야한다.
Loss는 실제 정답과 현재 출력의 차이로서 정의할 수 있는데 policy net의 정답은 바로 Optimal Policy가 되지만, 이는 현재 우리가 모르는 상태이기 때문에 optimal policy를 정답으로 사용할수는 없다.
따라서 policy optimization을 수행할 때는, 현재 policy $\pi_\theta$ 가 얼마나 좋은지를 평가하는 평가함수 $J(\theta)$ 를 정의하여 평가함수의 값을 최대화하는 방향으로 Gradient Ascent를 통해 갱신한다.

평가함수의 정의
- Q. 그렇다면 좋은 정책은 무엇일까?
- A. Return의 합이 가장 큰 정책!
  
  각각의 episode에 따라 최종적으로 받는 Return의 합은 달라질 수 있기 때문에, 기댓값을 이용하여 표현하면 다음과 같이 평가함수를 정의할 수 있다.
  $J(\theta) = \mathbb E_{\pi_\theta} \left[ \sum_t R_t\right]$
  Return의 합은 state-value function과 동일! (최종합이므로 start state에 대한 value function)
  $J(\theta) = \mathbb E_{\pi_\theta} \left[ \sum_t R_t\right] = v_{\pi_{\theta}} (s_0)$
  시작 state가 고정이 아니고 시작 state 또한 매번 다른 상태에서 시작한다면, start state에 대한 확률분포를 정의하여 이에 따른 확률 $\times$ 값; 기댓값 공식으로 표현한다.
  $J(\theta) = \sum_{s\in S}d(s) \times v_{\pi_\theta}(s)$
Gradient ascent 최대화가 목적이기 때문에 gradient와 같은 방향으로 update한다. $\theta' \leftarrow \theta + \alpha \nabla_\theta J(\theta)$

Policy Optimization : 1-step

1-step MDP로 문제를 간소화하고 생각하자. start state $s_0$ 에서 policy를 따라 하나의 action을 선택한 뒤 바로 Return을 받고 episode가 종료된다.

가능한 모든 action에 대한 return의 기댓값; action을 선택할 확률 $\times$ 보상으로 value function을 재정의할 수 있다.

J(\theta) = \sum_{s\in S}d(s) \sum_{a\in A}\pi_\theta(s, a)\times R_{s, a}

Gradient 도입

\nabla_\theta J(\theta) =\nabla_\theta \sum_{s\in S}d(s) \sum_{a\in A}\pi_\theta(s, a)\times R_{s, a}

우리의 문제는 Model-free이며 무한히 많은 state가 존재하기 때문에 위의 term으로는 계산할 수 없다. 샘플기반 방법론을 도입한다면 아래와 같이 수식을 변경하여 계산할 수 있다.

$d(s)$ 는 $\theta$ 와 관계없음
$\nabla_\theta J(\theta) =\sum_{s\in S}d(s) \sum_{a\in A} \nabla_\theta \pi_\theta(s, a)\times R_{s, a}$
분모 분자가 같은 값을 곱함 (=1이니까 수식자체에 변화는 없다)
$\nabla_\theta J(\theta) =\sum_{s\in S}d(s) \sum_{a\in A} \frac{\pi_\theta(s, a)} {\pi_\theta(s, a)}\nabla_\theta \pi_\theta(s, a)\times R_{s, a}$ $\nabla_\theta J(\theta) =\sum_{s\in S}d(s) \sum_{a\in A} \pi_\theta(s, a)\frac{\nabla_\theta \pi_\theta(s, a)} {\pi_\theta(s, a)}\times R_{s, a}$
$\ln x$ 의 미분을 이용하여 변경
1. $\frac{d }{dx} \ln x= \frac{1}{x}$
2. (양변 $\times dx$ ) ⇒ $d \ln x = \frac{dx}{x}$
$\nabla_\theta J(\theta) =\sum_{s\in S}d(s) \sum_{a\in A} \pi_\theta(s, a)\nabla_\theta \log\pi_\theta(s, a)\times R_{s, a}$
기댓값으로 표현
$\nabla_\theta J(\theta) =\mathbb E_{\pi_\theta} [\nabla_\theta \log \pi_\theta(s,a) \times R_{s,a}]$
⇒ 기댓값으로 표현되었기 때문에, $\pi_\theta(s,a)$ 를 따라 움직이는 Agent가 실제로 Environment와 상호작용하면서 기댓값을 계산하기 위해 사용할 샘플값을 여러개 모아 평균을 내어 gradient를 계산할 수 있다.

1-step이 아닌 일반적인 MDP에서는 return을 바로 받는 것이 아니라 리턴의 기댓값 q로 표현된다.

\nabla_\theta J(\theta) =\mathbb E_{\pi_\theta} [\nabla_\theta \log \pi_\theta(s,a) \times Q_{\pi_\theta}(s,a)]

3.3 REINFORCE

최초의 policy gradient method로 몬테카를로 기법을 이용한다. → episode 단위로 학습

action-value function의 정의에 따라 $Q_{\pi}(s,a) = \mathbb E_{\pi_\theta}[G_t|s_t=s,a_t=a]$ 로 표현될 수 있기 때문에 기댓값의 term 안에 $Q$ 를 $G_t$ 로 표현하여 넣어준다.

\nabla_\theta J(\theta) =\mathbb E_{\pi_\theta} [\nabla_\theta \log \pi_\theta(s,a) \times G_t]

Algorithm

3.4 PPO

PPO는 Gradient를 이용하여 학습하기 때문에 발생하는 REINFORCE 알고리즘의 단점을 해결하기 위해 고안된 알고리즘이다.

Needs for PPO
- REINFORCE의 단점 : episode 단위로 학습하기 때문에 한번에 결과가 반영되어서 각각의 step에 대한 중요도가 잘 표현되지 않는다. ⇒ MC의 단점을 그대로 가짐
- 작은 step이 아닌 가능한 큰 step만큼 갱신을 하면서도 어느정도는 기존의 policy를 유지하고 싶다. ⇒ Gradient가 너무 커서도, 너무 작아서도 안되게 조절하고 싶다!!

Formal Optimization

policy gradients : loss의 미분값 $\nabla_\theta J(\theta) =\mathbb E_{\pi_\theta} [\nabla_\theta \log \pi_\theta(s,a) \times \hat A_{\pi_\theta}(s,a)]$
obejective function
- gradient를 취하기 전 표현
  $J^{PG}(\theta) = \mathbb E_{\pi_\theta}[\log \pi_\theta(s,a)\times \hat A_{\pi_\theta} (s,a)]$
- probability ratio를 이용한 표현
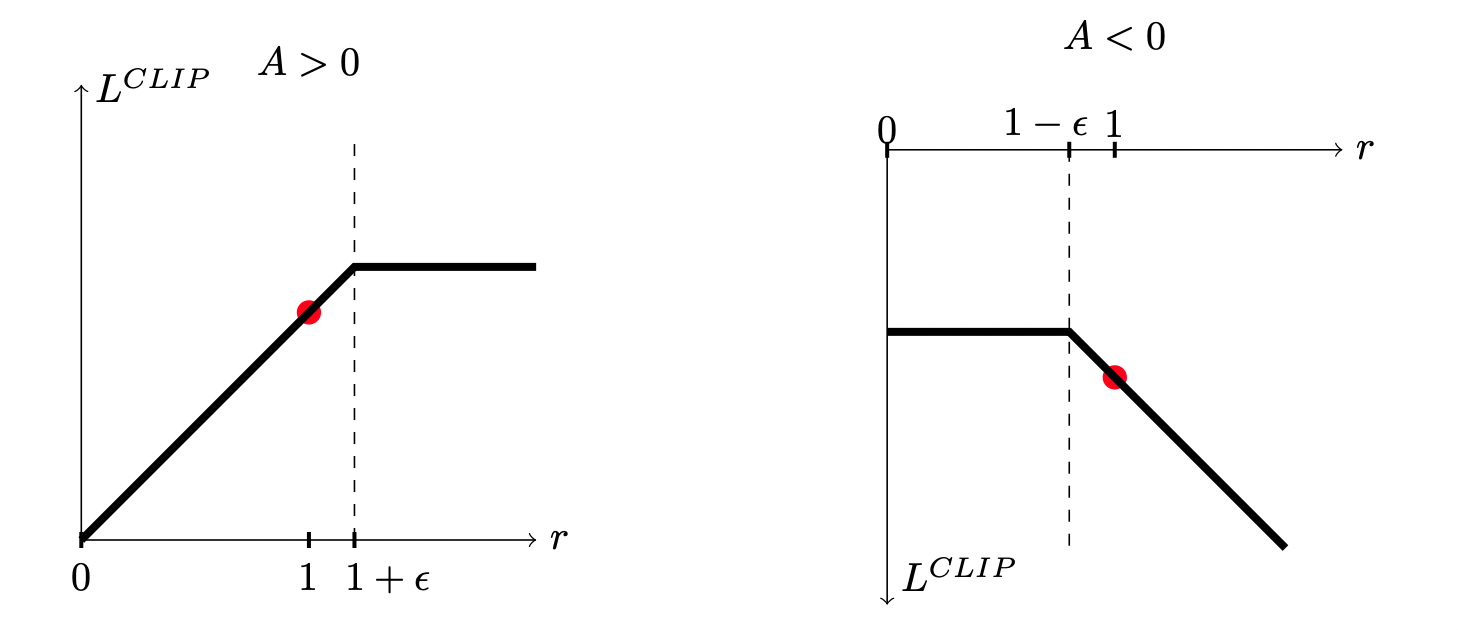
  $J_{\theta_\text{old}} (\theta) = \mathbb E_{\pi_\theta} \left[ \frac{\pi_\theta(s, a)}{\pi_{\theta_{old}}(s,a)} \hat A_{\theta_{old}}(s,a)\right]$

probability ratio old policy와 new policy 간의 probability ratio를 다음과 같이 정의할 수 있다. $r(θ)=\frac{\pi_θ(a|s)}{π_{θ_{old}}(a|s)}$ $θ_{old}$ 와 $θ$ 간의 차이에 대한 제한이 없다면, $J$ 를 maximize하기 위해 parameter $\theta$ 를 update할 때 극도로 커질 수도 있고 극도록 작아질 수도 있게 된다. 즉, 안정성이 매우 떨어지게된다.

PPO에서는 $r(θ)$ 가 1 이내의 작은 interval $[1−ϵ,1+ϵ]$ 사이의 값을 계속 가지도록 constraint를 추가함으로서 안정성을 유지할 수 있게 하였다. 원래의 값과, clip으로 다듬어진 probability ratio를 이용한 값 중에서 더 작은 값을 택한다.

⇒ 이로 인하여 더 많은 reward를 받기 위해 policy를 과하게 update하는 경우를 예방할 수 있다.

J^{\text{CLIP}} (\theta) = \mathbb E [\min (r(\theta) \hat{A}_{\theta_{old}}(s,a),\ \text{clip}(r(\theta), 1-\epsilon , 1+\epsilon) \hat A_{\theta_{old}}(s,a))]

Actor-critic Network
policy(actor)와 value-function(critic)간에 parameter를 공유하는 network 구조에 PPO를 적용할 때는 value function에 대한 error값과 entropy에 대한 term을 추가하여 exploration을 더 고려해준다. $J^{\text{CLIP}'}(\theta) = \mathbb E[J^{\text{CLIP}}(\theta) - c_1 (V_\theta(s) - V_{\text{target}})^2 + c_2 H(s, \pi_\theta(\cdot))]$

(사실 policy optimization은 헷갈리는부분이 아직 있어서 추후에 따로 더 공부할 생각이다)

Reference

OpenAI
[RL] Policy Gradient Algorithm
바닥부터 배우는 강화학습, 노승은
심층 강화학습 인 액션

Vaughan

우주의 아름다움도 다양한 지식을 접하며 스스로의 생각이 짜여나갈 때 불현듯 나를 덮쳐오리라.