
본 포스팅은 David Silver 교수님의 강화학습 강의와 그 강의를 정리한 팡요랩 강의를 바탕으로 정리한 것입니다.
문제를 해결하기 위해서는 먼저 문제를 잘 정의하는 것에서부터 시작하여야한다.
대부분의 강화학습 문제는 Environment를 MDP로 formal하게 표현할 수 있다.(fully observable) 그렇다면 MDP는 무엇이며, MDP를 풀기 위해서는 어떻게 해야하는가?
1. Markov Processes : MP
1.1 Markov Property
✂️ “The future is independent of the past given the present”
-
Definition of Markov Property
A state is Markov if and only if- 시작 state 에서부터 현재 state 까지 도달할 확률이 바로 이전 state 에서 현재 state 까지 도달할 확률과 같은 state를 Markov state라고 한다.
- 이전 state만 알 수 있다면, 이전까지의 모든 history는 잊어버려도 된다.
- 강화학습의 문제는 기본적으로 MDP로 표현하기 때문에 Markov Property를 따른다고 가정한다.
-
State Transition Matrix
-
Basic Markov Process에서는 action 없이, 매번의 time-step마다 state를 확률에 기반하여 옮겨다니게 된다.
-
Markov state 에서 로 transition할 probability은 다음과 같이 정의된다.
-
가능한 모든 state 와 pair를 원소로 갖는 matrix로 표현할 수 있다. (matrix의 각각의 row의 합은 1)
-
1.2 Definition of Markov Processes
- Definition of Markov Processes
A Markov Process is a tuple- is a (finite) set of states
- is a state transition probability matrix,
- Markov process는 memoryless random process이다.
- memoryless는 내가 지금까지 어떤 경로를 따라 도달했는지 상관없이 state s에 도달한 순간, 를 결정할 수 있다.
- random process는 동일한 state에서 시작하더라도 어떤 state를 거치는지에 따라 여러가지 episode를 샘플링을 할 수 있다는 뜻이다.
→ 즉, random한 state들의 sequence 는 Markov property를 따른다!
1.3 Example of Markov Processes
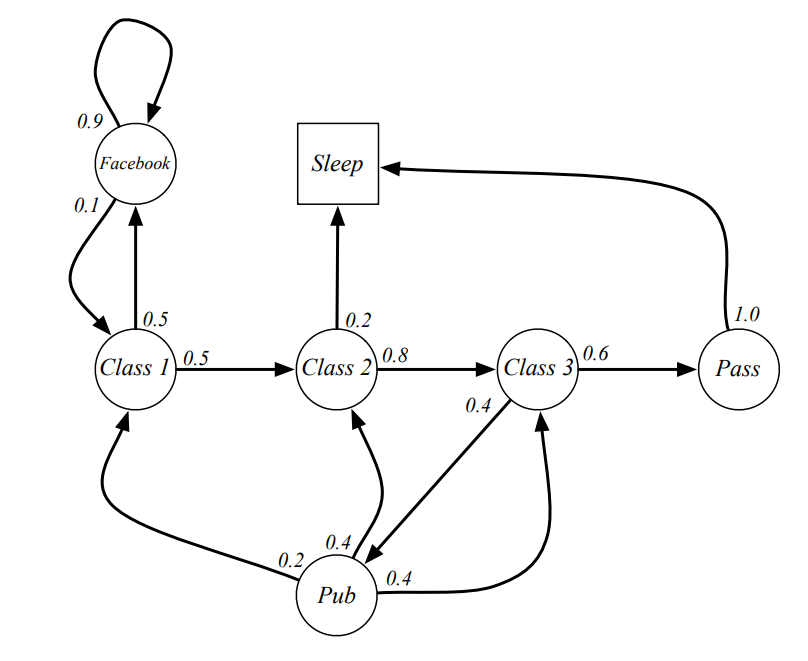
- 위와 같은 model에서 에서 시작하는 Sample episode는 다음과 같은 것들이 있을 수 있다.
- C1 → C2 → C3 → Pass → Sleep
- C1 → FB → FB → C1 → C2 → Sleep
- C1 → C2 → C3 → Pub → C2 → C3 → Pass → Sleep
- C1 → FB → FB → C1 → C2 → C3 → Pub → C1 → FB → FB → FB → C1 → C2 → C3 → Pub → C2 → Sleep
- Model의 Edge에 표기된 probability를 바탕으로 다음과 같은 Transition Matrix를 정의할 수 있다.

2. Markov Reward Processes : MRP
2.1 Definition of Markov Reward Processes
- Definition of Markov Reward Processes
A Markov Reward Process is a tuple
- is a finite set of states
- is a state transition probability matrix,
- is a reward function,
- is a discount factor,
- Reward
- state의 변화에 따른 reward를 “environment”가 Agent에게 알려준다.
- MRP에서는 현재 state 에 도달하면 Reward 을 제공한다.
- Agent는 immediate reward 뿐만 아니라, 이후로 얻게되는 미래의 reward까지 고려한다. (with discount)
2.2 Value function
-
Definition of Return
The return is the total discounted reward from time-step
-
discount
- time-step이후의 reward는 의 reward로 표현된다.
- immediate reward가 delayed reward보다 더 큰 영향을 줄 수 있게 한다.
-
값에 따른 효과*
- 에 가까울수록 “myopic” evaluation (근시안적)
- 에 가까울수록 “far-sighted” evaluation (미래지향적)
-
why discount?
discount가 없을 때 발생할 수 있는 문제점
- infinite한 time-step을 가질 때, 매 time step마다 0.1의 reward를 받는 episode와 1의 reward를 받는 episode를 구분할 수 없다. ( 크기비교 불가)
- Agent가 시작할 떄 1을 받은 경우와 종료할 때 1을 받은 경우 둘 중에 어떤 episode가 더 나은지를 판단할 수 없다.
-
-
Definition of Value Function
The state value function of an MRP is the expected return starting from state
- 현재 state 에서 Return에 대한 기댓값으로 value function을 정의할 수 있다.
2.3 Bellman Equation for MRPs
- Bellman Equation
-
value function은 다음의 2가지 part로 분리할 수 있다.
- immediate reward
- discounted value of successor state
-
유도과정
-
-
Bellman Equation의 직관적인 이해
-
Bellman Equation
현재 state 가 transition할 수 있는 다음 state 들의 후보는 여러가지가 있을 수 있다. 여러가지 후보 중에서 “확률”에 따라 next state를 결정하게 된다. 따라서 가능한 여러가지 episode들에 대한 기댓값으로서 리턴을 계산하며, 이 때 같은 value-function을 사용하여 재귀 형태로 표현할 수 있게된다.
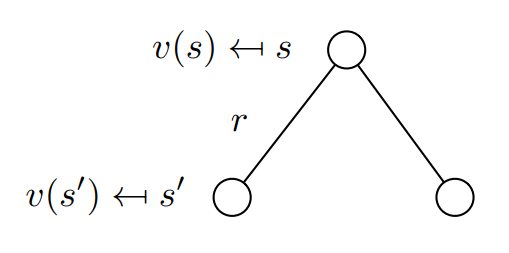
-
Expectation을 제거한 형태
- MRP에서 1-step Reward는 현재의 state 에 따라 고정된 상수이기 때문에 그대로 빠져나온다.
- 는 next state s’가 무엇인지에 따라 달라지는 값이기 때문에 Expectation을 적용한다.
*Definition of Expectation : probability value
-
-
for Matrix Form
is a column vector with one entry per state*
-
solving Bellman Equation
⇒ Bellman Equation을 linear equation으로 표현하여 directly solve할 수 있다!
-
단점
- 단, computational complexity가 이다.
- state가 커질수록 계산량이 매우 커지기 때문에 direct solution은 small MRPs에만 적용한다.
-
대부분의 경우 MRPs는 iterative method를 이용하여 해결한다.
- Dynamic Programming
- Monte-Carlo evaluation
- Temporal-Difference learning
여기서 소개된 iterative method는 MDP를 solve하기 위해서 사용되는 방법이기도 하다. MRP와 달리 MDP는 directly solve를 위한 방법이 존재하지 않기 때문에, iterative method를 채택한다.
-
2.4 Example of MRPs
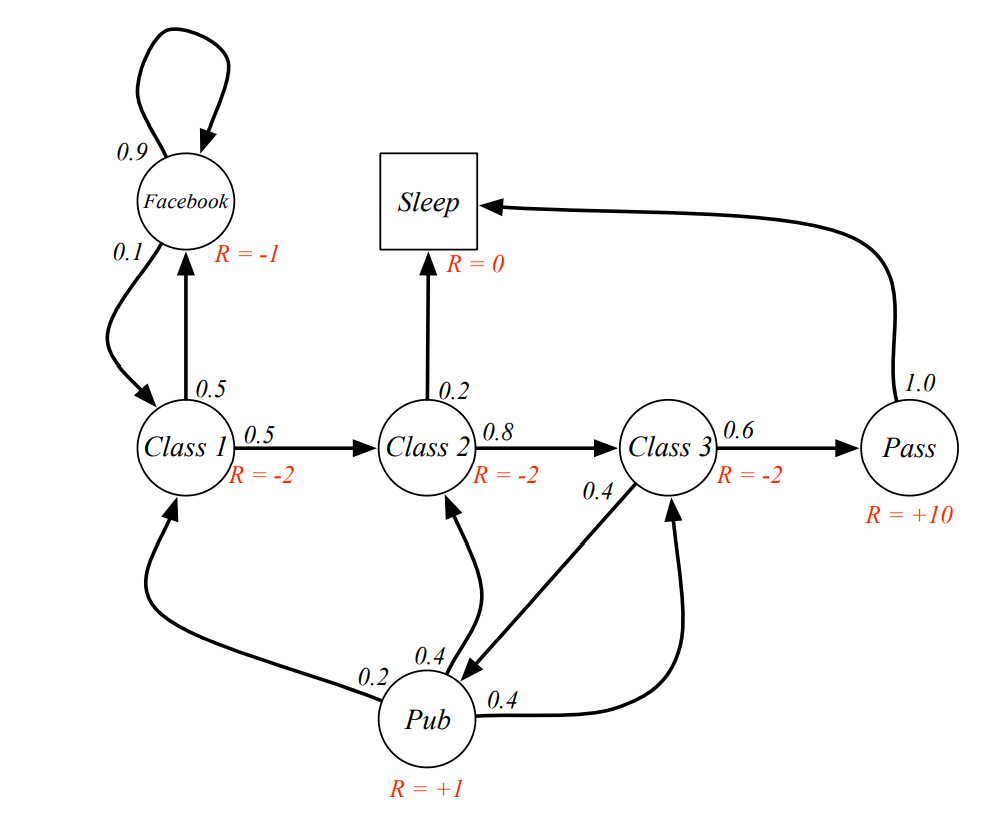
-
Sample returns for Student MRP
starting from with 일 때, 각각의 sample episode들에 대한 Return은 다음과 같이 계산될 수 있다.
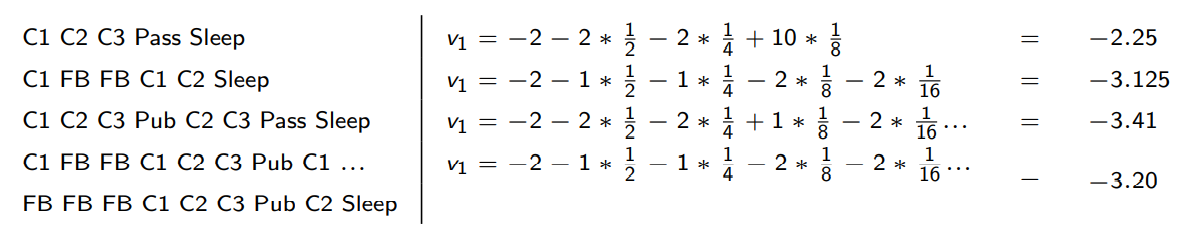
-
discount value에 따른 state value의 변화
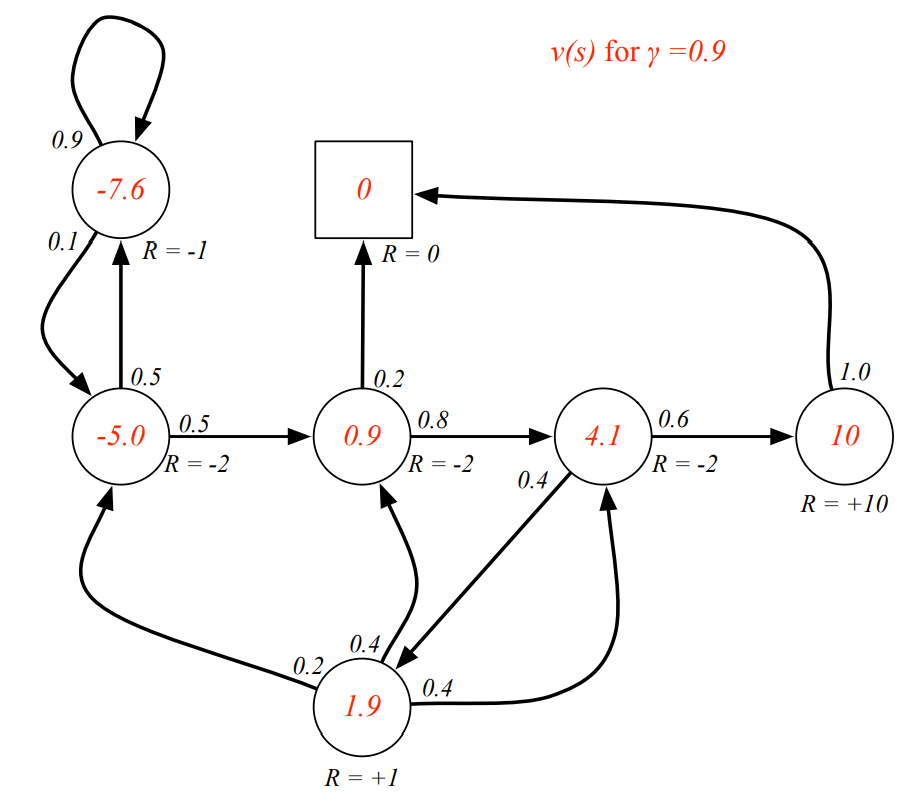
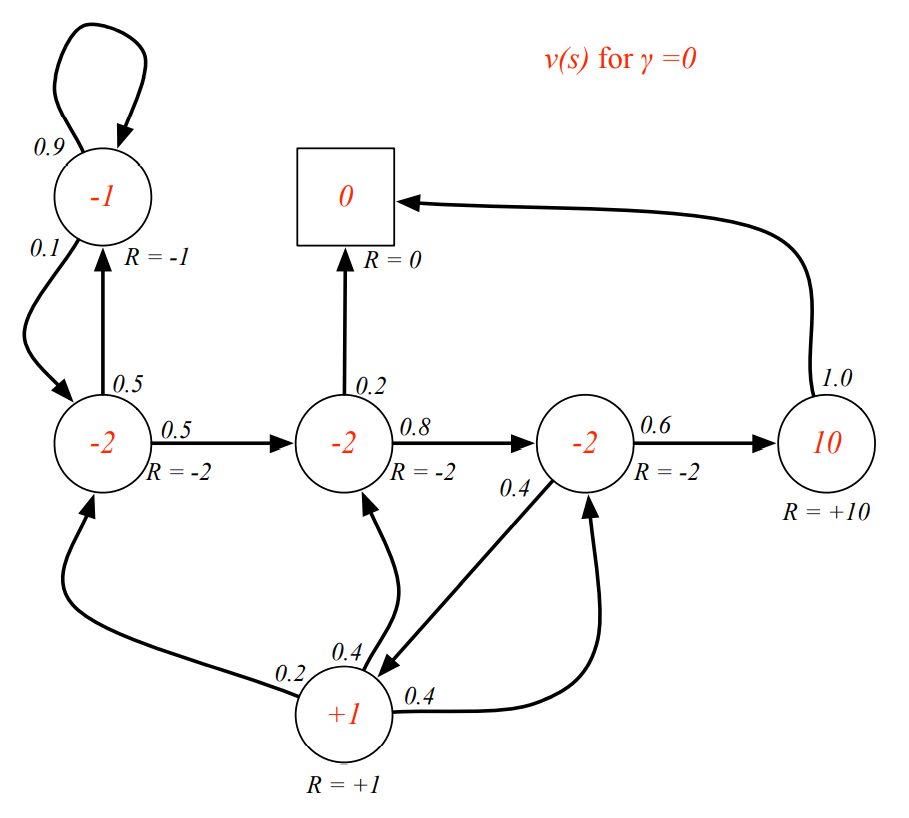
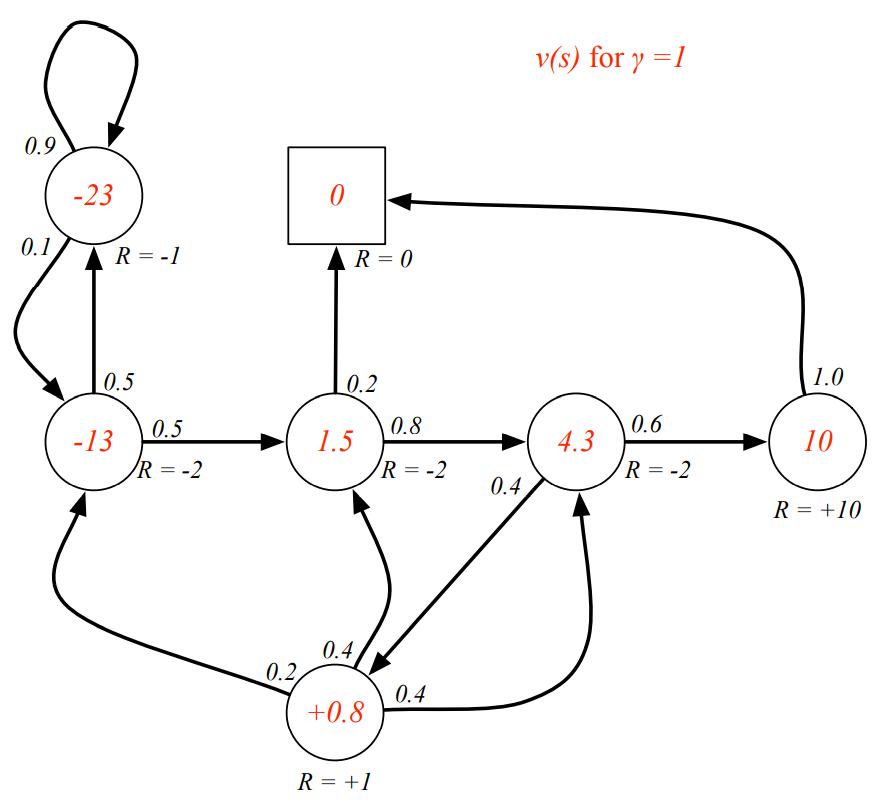
-
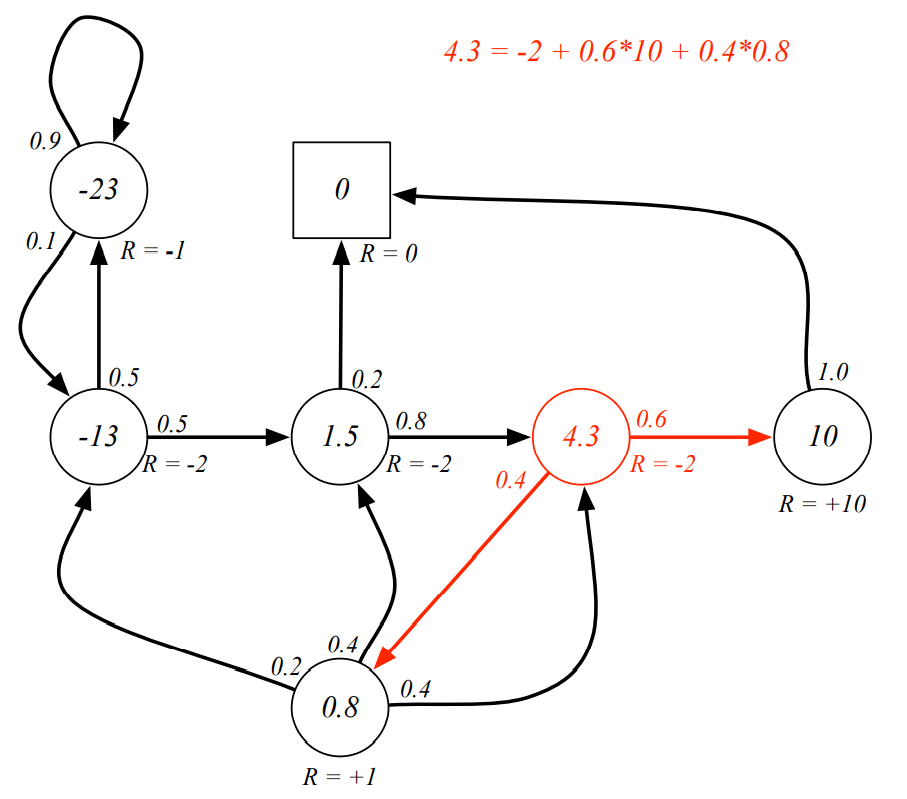
Bellman Equation
Q. 빨간색 state의 value가 이라고 알려져 있을 떄, Bellman Equation을 만족하는가?
3. Markov Decision Processes : MDP
3.1 Definition of Markov Decision Processes
MP, MRP에서는 state의 변화가 오로지 Environment의 transition probability 에 의해 결정되었다.
그러나 MDP에서는 state의 변화가 Agent의 Action 에 의해 결정되게 된다! (다만, 여전히 환경의 불안정함은 존재)
- Definition of Markov Reward Processes
A Markov Reward Process is a tuple
- is a finite set of states
- is a finite set of actions
- is a state transition probability matrix, → state 에서 action 를 취할 때, state 에 도달할 확률 (환경의 불안정함)
- is a reward function,
- is a discount factor,
- state transition probability
- Agent가 어떠한 Action을 취했을 때, Agent가 인식하는 state가 deterministic하게 결정되지 않고 “확률”적으로 정해지게 된다.
- 또한 해당 state에서 그 Action을 할 확률도 정해진다.
- Example) 무인이동체가 우회전이라는 action을 결정했지만, 그 순간 빨간불로 신호가 바뀌어 우회전을 하지 못하고 정지하는 경우
3.2 Policy & Value function
-
Definition of Policy
A policy is a distribution over actions given states,
- state 에서 action 를 수행할 확률 분포
- Agent는 policy를 따라서 어떤 action을 선택할지를 결정하게 된다.
- MDP의 policy는 agent가 지금까지 겪어온 history가 아닌, 오직 current state에 의해서만 의존한다.
- Policies are stationary (time-independent)
-
(번외) policy와 MDP를 이용하여 MRP로 표현하기
MDP에서 Agent의 policy가 고정이라면 Agent가 없는 Markov Process로 표현할 수 있다.
Given an MDP and a policy
- State sequence → Markov process 로 표현할 수 있다.
- State and Reward sequence → Markov reward process 로 표현할 수 있다.
*where : policy가 고정되어있다면, 어떤 action 선택하고-transition probability에 따라 최종적으로 어떤 state가 next state가 되는지를 확률로서 계산할 수 있다.- transition probability : 으로 갈 확률은 각 action의 확률 action 를 했을 때 로 갈 확률의 합(기댓값)
- reward : 의 return은 각 action의 확률 action 를 했을 때 의 reward의 합(기댓값)
-
Value Function
-
어떤 “policy” 를 따라 episode를 진행하는지에 따라 value가 달라질 수 있기 때문에, Agent가 어떻게 행동하는지를 나타내는 policy 를 함께 기술해야한다.
-
Definition of state-value function
The state value function of an MDP is the expected return starting from state , and then following policy
-
Definition of action-value function
The action value function is the expected return starting from state , taking action , and then following policy
- 현재 state 에서 선택하는 action 는 policy를 따라 선택한 것이 아닐수도 있다! 단, 이후 episode를 진행할 때는 policy 를 따라 진행하게 된다.
- action-value function이 정의된다면, Agent가 어떤 action을 선택할 지 결정할 때 Action value function의 값을 보고 선택하기만 하면된다.
⇒ 즉, 문제를 간단하게 표현할 수 있다.
(state value function을 사용하면 다른 state들의 value function을 알아야하며, 그때 어떤 action을 했을 때 로 가게될 확률도 알고 있어야한다.)
- Q-learning이나 DQN같은 곳에서 사용하는 Q가 바로 action-value function을 의미한다.
-
3.3 Bellman Expectation Equation
MRP에서 value function을 2가지 part(immediate reward, discounted value)로 분리했던 과정을 동일하게 적용하면 MDP에서도 초기 Bellman Equation을 쉽게 얻을 수 있다.
-
Bellman Expectation Equation (초기)
- Bellman Expectation Equation for
에서의 state-value는 를 따라** 1-step 수행하여 받은 reward와 next-state 에서의 value의 합의 기댓값과 동일하다.
-
state와 action의 관계 - (1)
- state의 value는 그 state에서 가능한 모든 action()에 대한 action-value의 기댓값과 동일하다.
- action의 선택은 오로지 policy에 의존하기 때문에 확률분포에 따라 episode별로 선택된 action이 달라지고 따라서 reward가 변화하여 정확한 값을 모르기 때문에 기댓값 형태로 표현해야한다.
- state-value function의 definition이 policy에 의해 선택된 action에 대한 가능한 모든 episode의 리턴의 기댓값이기 때문에 Q-function으로 표현할 수 있다.
→ 에 대한 기댓값의 다른 표현
- Bellman Expectation Equation for
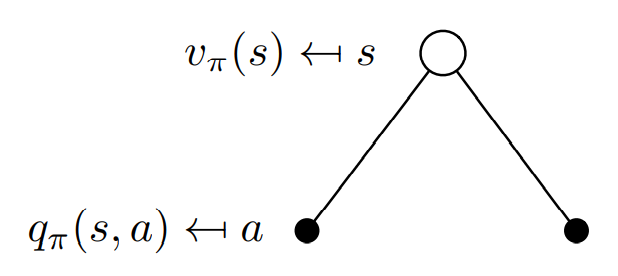
-
Bellman Expectation Equation for
에서 action 를 선택하여 받은 action-value는 를 선택해 1-step 수행하여 받은 reward와 next-state 에서의 action-value의 합의 기댓값과 동일하다.
-
action과 state의 관계 - (2)
-
action의 value는 action을 수행함으로써 전달받는 1-step reward 과 가능한 모든 next-state()에 대한 state-value의 (감쇄)기댓값의 합과 동일하다.
-
특정 action 를 수행하면 그 때 받게되는 reward의 값을 확실하게 알 수 있기 때문에 immediate rewrd를 이용하여 표현한다.
-
Bellman Expectation Equation에서 Expectation 를 제거한 형태
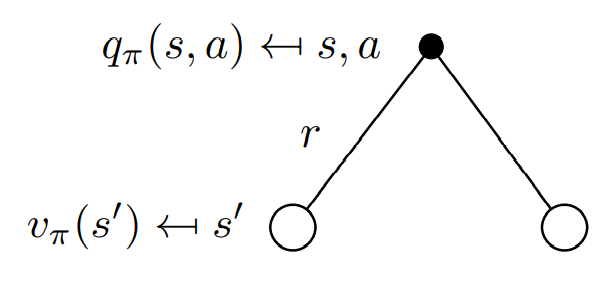
-
-
-
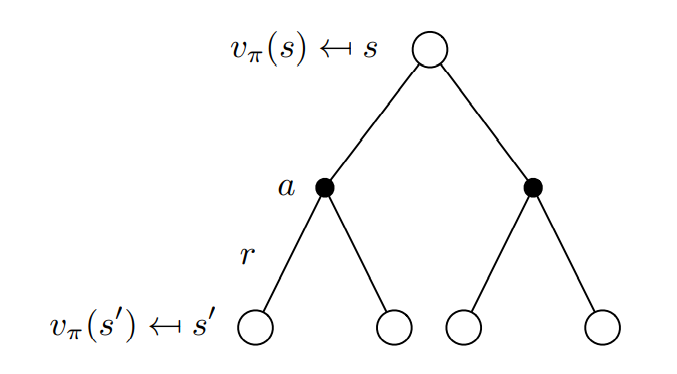
Bellman Expectation Equation [재귀]
MRP에서의 Bellman Equation과 달리, MDP에서는 action의 존재로 인하여 가장 초기의 Bellman Equation을 바로 재귀적으로 표현하기 힘들다. 따라서 action-value와 state-value간의 관계를 이용하여 재귀적 표현으로 Bellman Expectation Equation을 표현한다.
→ 그대로 관계식을 대입한다!
-
Bellman Expectation Equation for
-
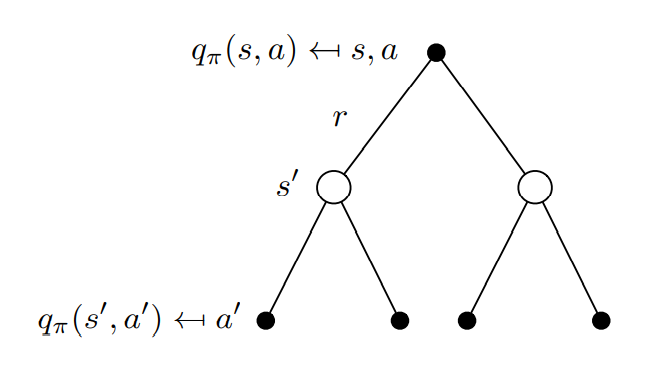
Bellman Expectation Equation for
-
- for Matrix Form
*MDP에서 Agent의 policy가 고정이라면 Agent가 없는 MRP로 표현할 수 있기 때문에, 그대로 matrix form을 적용해서 direct solution을 얻을 수 있다.with direct solution
3.4 Example of MDPs
-
MDP의 예시 : Action에 대하여 reward가 제공된다
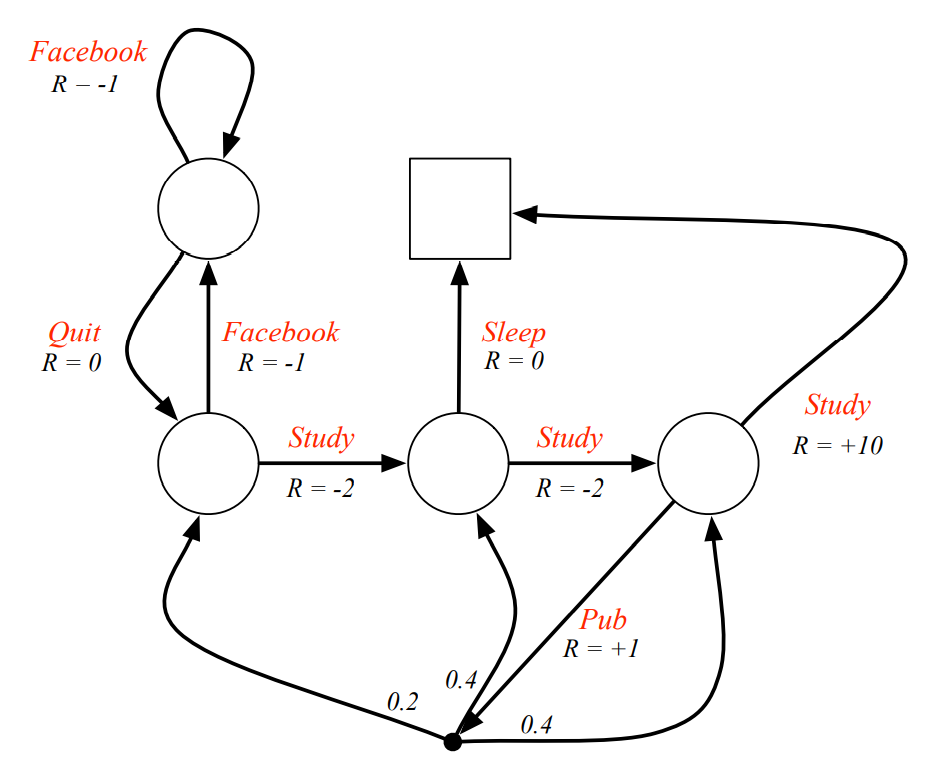
-
MDP에서 state-value function의 계산
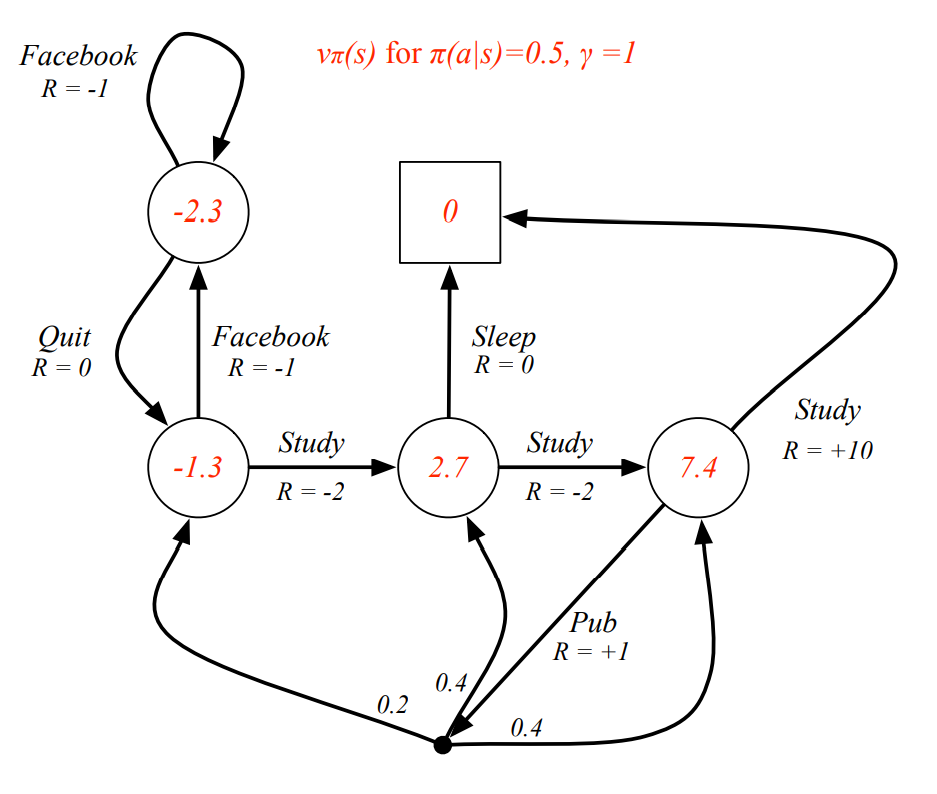
- Bellman Expectation Equation Q. 빨간색 state의 value가 라고 알려져 있을 떄, Bellman Expectation Equation을 만족하는가?
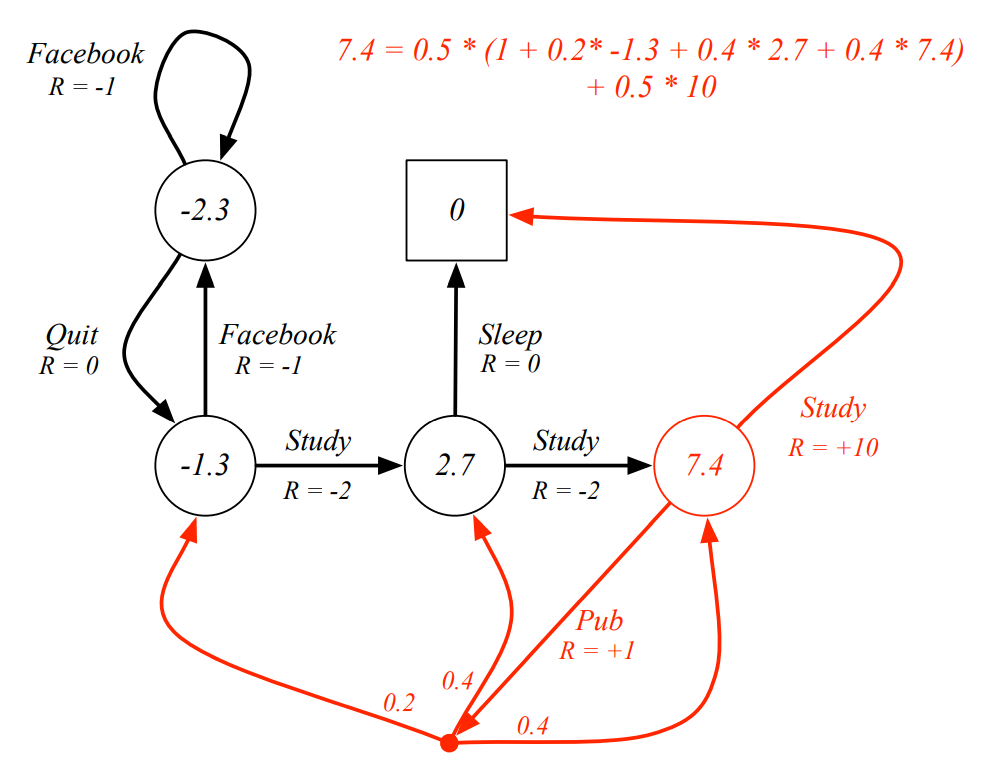
4. Optimal Solution
4.1 Optimal Value Function
-
Definition of Optimal Value Function
가능한 모든 policy에 대하여 계산했을 때, 그 중에서 가장 maximum 값을 갖는 value function
- Definition of optimal state-value function
The optimal state value function is the maximum value function over all policies
- Definition of optimal action-value function
The optimal action value function is the maximum action-value function over all policies
- Definition of optimal state-value function
-
Optimal Value Function
- optimal value function은 MDP에서 가능한 최고의 성능을 나타낸다.
- 해당 MDP의 optimal value function을 찾았다면, 그 MDP는 “solved”되었다고 한다.
- 일반 value function과 달리 bellman optimality eqation은 matrix form으로 표현되지 않기 때문에 directly solve가 불가능하다.
-
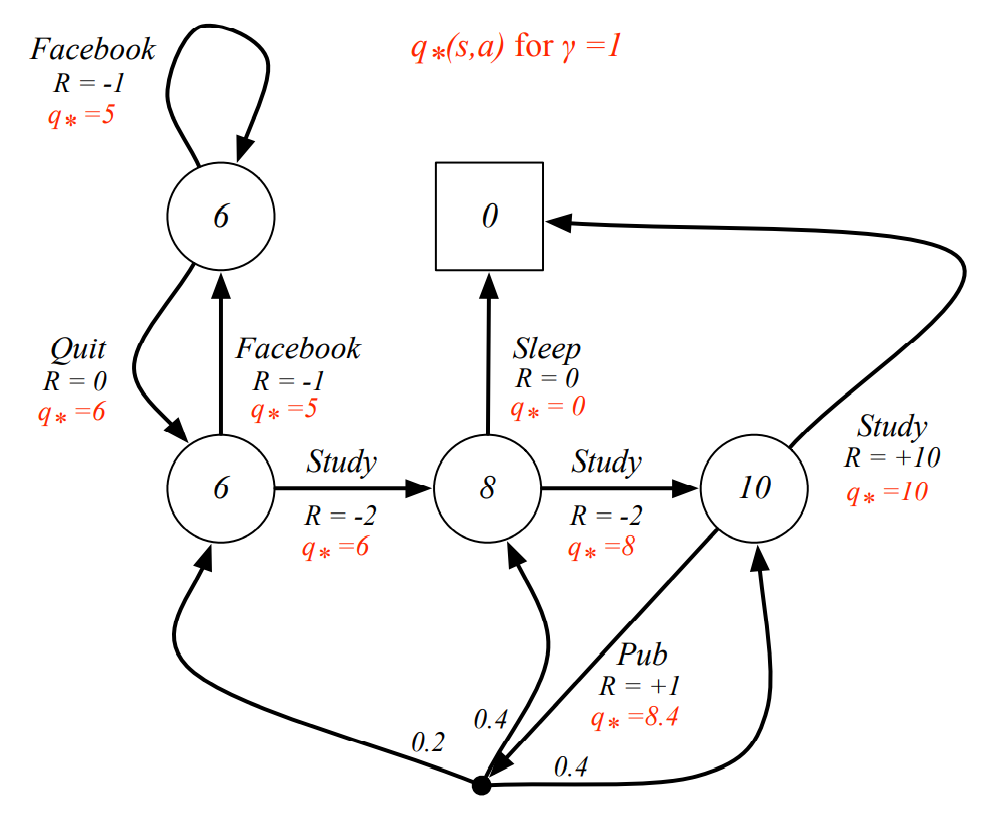
Example
optimal policy를 따랐을 때, state-value function과 action-value function
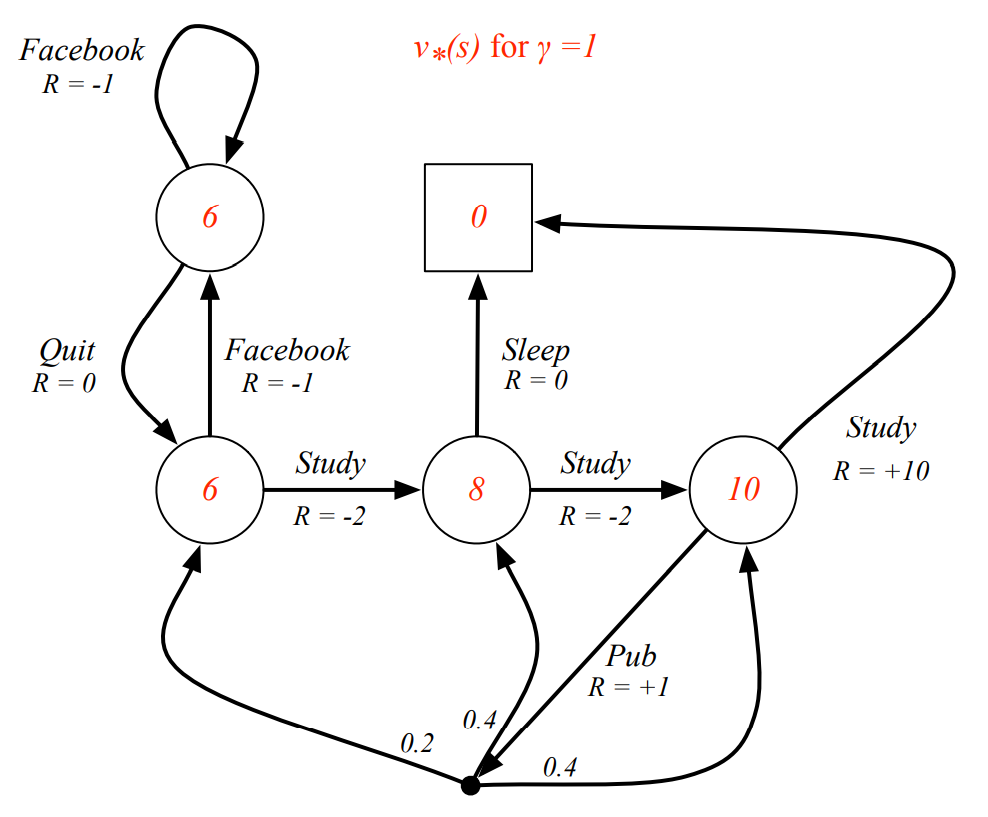
4.2 Optimal Policy
-
policy간의 partial ordering
모든 state에 대하여 가 보다 같거나 크다면, 가 보다 더 나은 policy 라고 말할 수 있다.
-
Theorem of policy
For any Markov Decision Process
- 다른 모든 policy보다 더 같거나 좋은 optimal policy 가 존재한다.
- optimal policy를 따르는 value function은 optimal value function과 동일하다
- 모든 optimal policy는 그 optimal policy를 따르는 optimal value function을 가진다.
- 모든 optimal policy는 그 optimal policy를 따르는 optimal action-value function을 가진다.
- 모든 optimal policy는 그 optimal policy를 따르는 optimal value function을 가진다.
-
Optimal Policy를 찾는 방법
-
optimal action-value function에 대하여 max가 되게하는 action만을 계속해서 취하는 policy
-
즉, optimal action-value function 을 알고있다면 그 즉시 deterministic optimal policy를 구할 수 있다. ⇒ MDP를 solve!
deterministic
- 원래 policy는 각각의 action을 수행할 확률로 정의되기 때문에 stochastic하다.
- 그러나 optimal action-value function을 사용하여 구한 optimal policy는 하나의 action만을 하도록 결정된 deterministic한 policy이다.
-
-
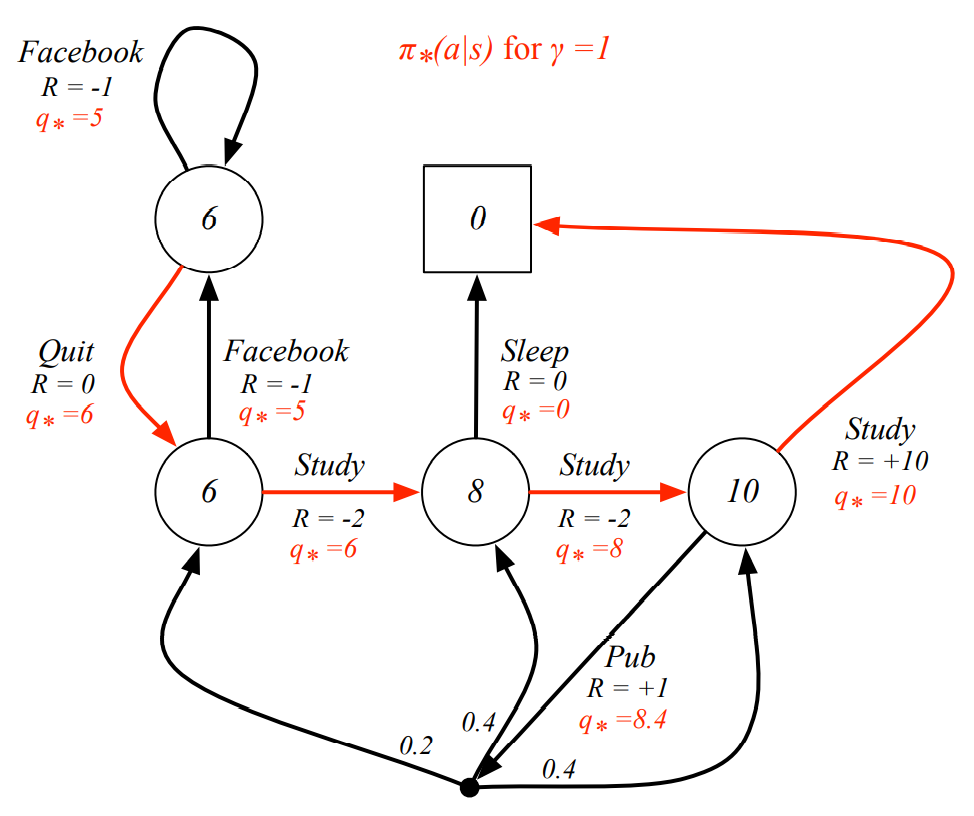
Example : Optimal Policy
4.3 Bellman Optimality Equation
기본적으로 Bellman Expectation Equation과 동일한 구조를 이룬다. 다만, optimal policy를 알지 못하여 모든 수식을 Expectation으로부터 표현하기 시작했던 것과 달리 여기서는 optimal policy 를 알고있기 때문에 이를 이용하여 equation을 표현한다.
-
Optimal state-value function과 Optimal action-value function의 관계
-
state과 action의 관계 - (1)
-
state 의 optimal value는 그 state에서 optimal action-value가 최대가 되게하는 action 을 취했을 때의 optimal action value와 동일하다.
-
action-value를 maximize하는 action을 선택하는것이 optimal하기 때문에 자명하다.
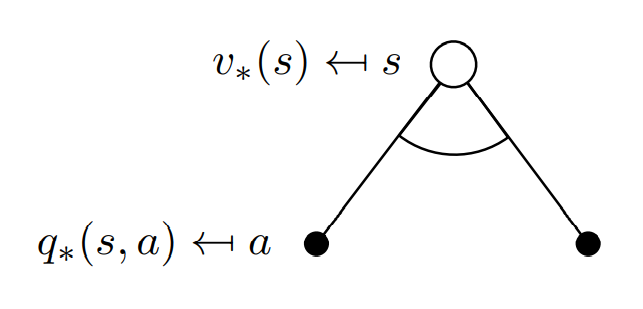
-
-
action과 state의 관계 - (2)
-
(state 에서) action 의 optimal value는 action을 수행함으로써 전달받는 1-step reward 과 가능한 모든 next-state()에 대한 optimal state-value의 (감쇄)기댓값의 합과 동일하다.
-
action을 하더라도 그 다음 state가 무엇으로 결정되는지는 환경의 불안정성(=state probability)를 따르기 때문에 기댓값의 형태로 표현한다.
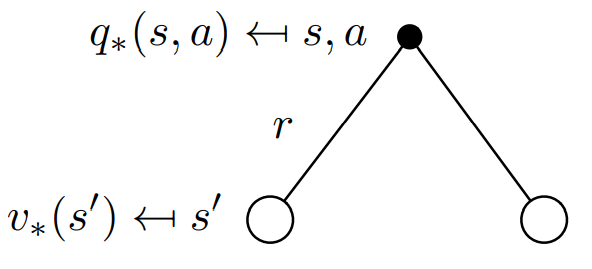
-
-
-
Bellman Optimality Equation [재귀]
-
Bellman Optimality Equation for
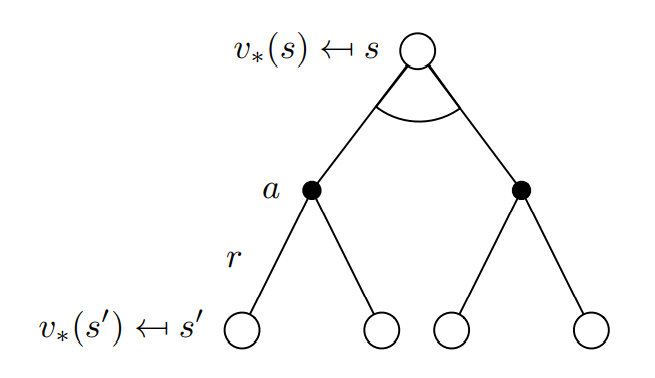
-
Bellman Optimality Equation
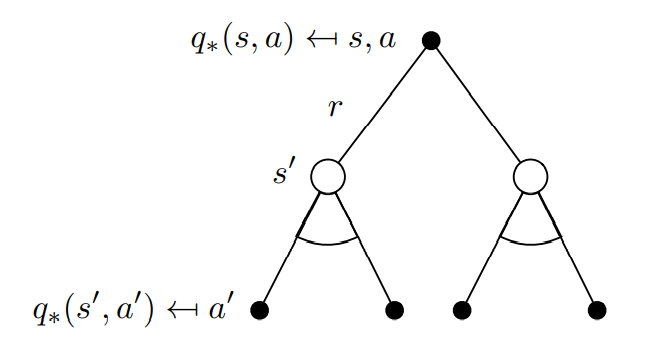
-
-
Example
Q. 빨간색 state의 value가 이라고 알려져 있을 떄, Bellman Optimality Equation을 만족하는가?
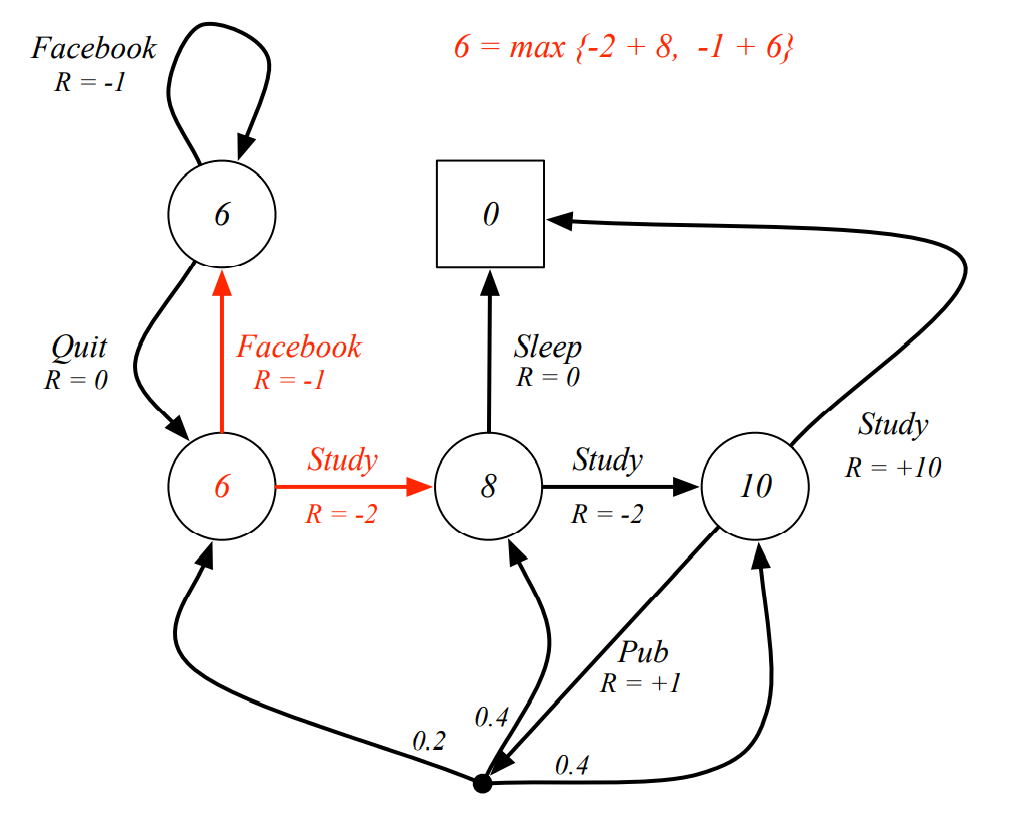
-
Bellman Optimaliy Equation을 푸는 방법
- Bellman Optimally Equation은 non-linear equation이다. ( 때문) ⇒ 따라서 closed form solution을 가지지 았는다. (in general)
- Many iterative solution methods
- Value Iteration (DP)
- Policy Iteration (DP)
- Q-learning
- SARSA
- Bellman Optimally Equation은 non-linear equation이다. ( 때문) ⇒ 따라서 closed form solution을 가지지 았는다. (in general)
