본 포스팅은 David Silver 교수님의 강화학습 강의와 그 강의를 정리한 팡요랩 강의를 바탕으로 정리한 것입니다.

Planning이란?

→ Environment; MDP를 알고 있을 때 더 나은 policy를 찾아나가는 과정

1. Dynamic Programming

---

1.1 Dynamic Programming 이란?

⚙ Dynamic Programming

• Dynamic : sequential or temporal component to the problem
• Programming : optimising a “program”

하나의 큰 문제를 바로 해결하기 힘들 때, 여러개의 작은 부분 문제들로로 문제를 나누고 부분 문제들의 해를 모두 구한 뒤에 그 해를 이용해서 더 큰 크기의 부분 문제를 해결하는 과정을 거쳐 문제를 해결하는 하나의 방법론

1.2 Dynamic Programming의 요구조건

• Optimal substructure : 하나의 큰 문제에 대한 solution은 여러개의 작은 부분문제들의 solution으로 분할 할 수 있어야 한다.

• Overlapping subproblems : 어떤 부분문제의 해는 상위의 부분문제를 해결하기 위하여 여러번 사용될 수 있다. 따라서 보통 부분문제의 해들을 저장해두고 가져와서 이용한다.
  ⇒ Markov decision processes satisfy both properties!

  • Bellman equation은 재귀적으로 표현된다.
  • value function이 계산한 value는 저장해두었다가 Policy를 평가/갱신하기 위해 사용된다.

1.3 Planning by DP

• DP를 이용하여 planning을 수행할 때는, MDP에 대한 모든 정보$^{[1]}$를 알고있다고 가정한다.
  [1] MDP의 정보

  1. state transition probability
  2. reward

• 강화학습 문제의 종류에 따른 표현

  • prediction

    MDP와 policy가 주어졌을 때, 그 policy$^{[2]}$를 따라 Agent가 수행했을 때의 value function을 계산하는 문제

    • input : MDP $<\mathcal S, \mathcal A, \mathcal P, \mathcal R, \gamma>,\ \pi$ (=or $<\mathcal S, \mathcal P^\pi, \mathcal R^\pi, \gamma>$)
    • output : value function $v_\pi$

    [2] 이때 주어지는 Policy는 optimal policy여야하는 조건같은건 가지고 있지 않는다.

  • control

    MDP가 주어졌을 때, optimal value function, policy를 찾는 문제

    • input : MDP $<\mathcal S, \mathcal A, \mathcal P, \mathcal R, \gamma>$
    • output : optimal value function $v_*$, optimal policy $\pi_*$

2. Policy Evaluation

Policy가 고정되어있을 때, value-function을 게산하는 과정

---

2.1 Iterative Policy Evaluation

• 문제 정의

  • problem : 주어진 어떤 policy $\pi$를 평가하는 것, 즉 policy를 따랐을 때의 value function $v_\pi(s)$를 찾는 것을 목적으로 한다. [prediction]

  • solution : Bellman expectation equation을 이용하여 iterative한 방법을 적용한다.

    $v_{1;\ init} → v_2 → \cdots → v_\pi$
    

• synchronous backup

  1. each iteration k+1

     2. for all states $s \in \mathcal S$

        3. update $v_{k+1}(s)$ from $v_k (s')$

           → 전 단계 $k$에서의 value f를 이용하여 현재 단계 $k+1$에서의 value를 갱신한다.

           (where $s'$는 $s$에서 갈 수 있는 가능한 모든 state)

     → 이 과정을 반복하면 $v_\pi(s)$에 수렴하게 된다.

• Bellman Expectation Equation

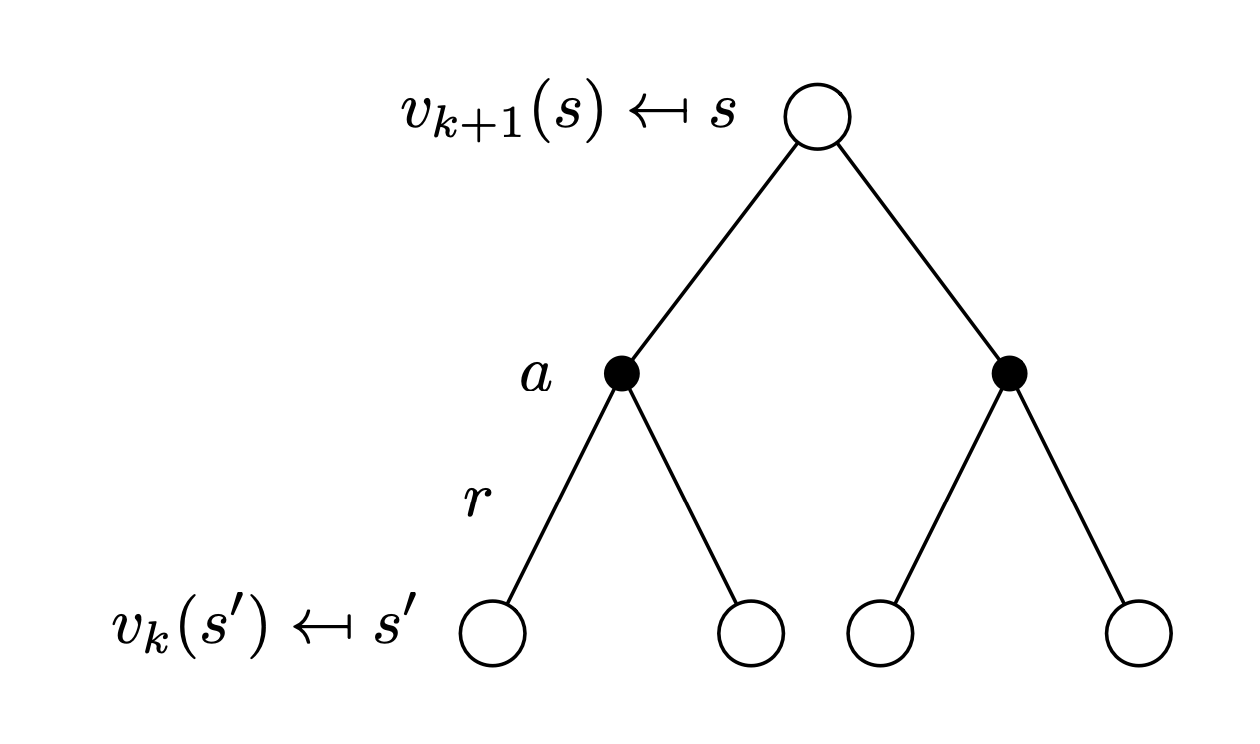
  • $k+1$ 단계에서는 $k$단계에서보다 더 정확한 value 값을 가지게 하고 싶어한다.
  • evaluate하는 state $s$에서 갈 수 있는 가능한 모든 state $s'$에서의 value를 사용하여 갱신해준다.
  • next state의 value일수록 지금까지 policy를 따라 진행하면서 실제로 얻은 정확한 reward $r$의 값이 더 많이 존재하기 때문에 점점더 정확한 value를 가지게 된다.
  • 따라서 가장 초기 init 상태일 때의 value function의 값은 모두 정확하지 않더라도 정확한 값인 “reward”가 고려되기 때문에 최종적으로 $v_\pi(s)$에 수렴할 수 있게 된다.

2.2 Example with Gridword

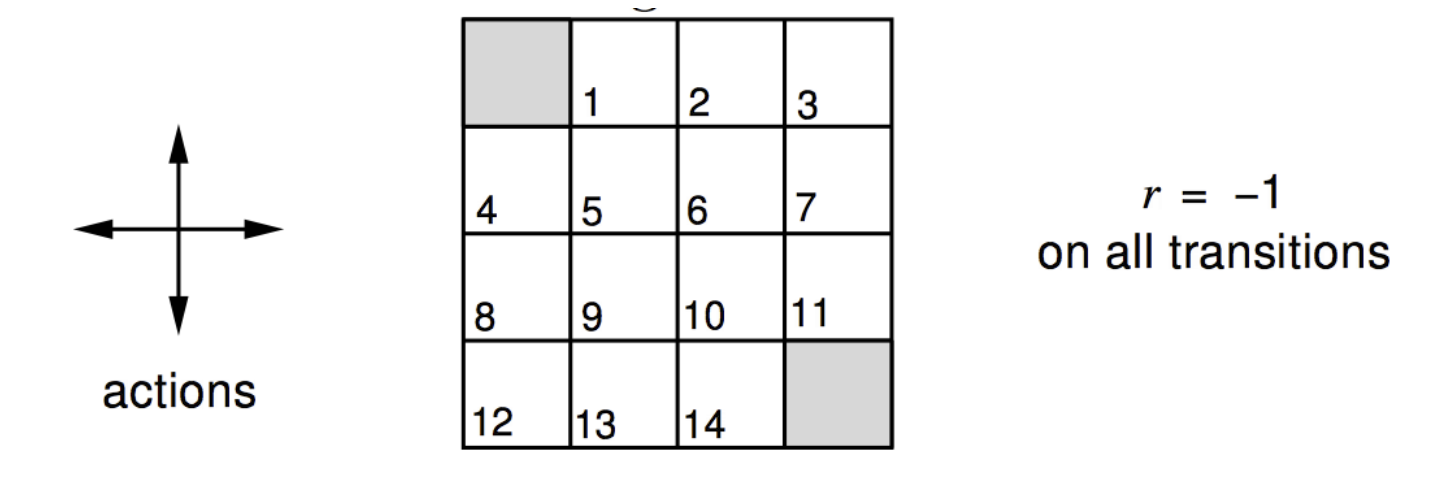
• *Gridworld for prediction

  • MDP

    • 1~14는 nonterminal state이고, 왼쪽 위 또는 오른쪽 아래에 하나의 terminal state를 가진다.

    • $\gamma = 1$ (미래지향적)

    • terminal state에 도달하기 전까지 항상 $-1$의 reward를 받는다.

      

  • random policy
    $\pi(n|\cdot)=\pi(s|\cdot)=\pi(w|\cdot)=\pi(e|\cdot)=0.25$
    

• Iterative Policy Evaluation

  • ex) $k=0$
    일 때 6번 state의 갱신과정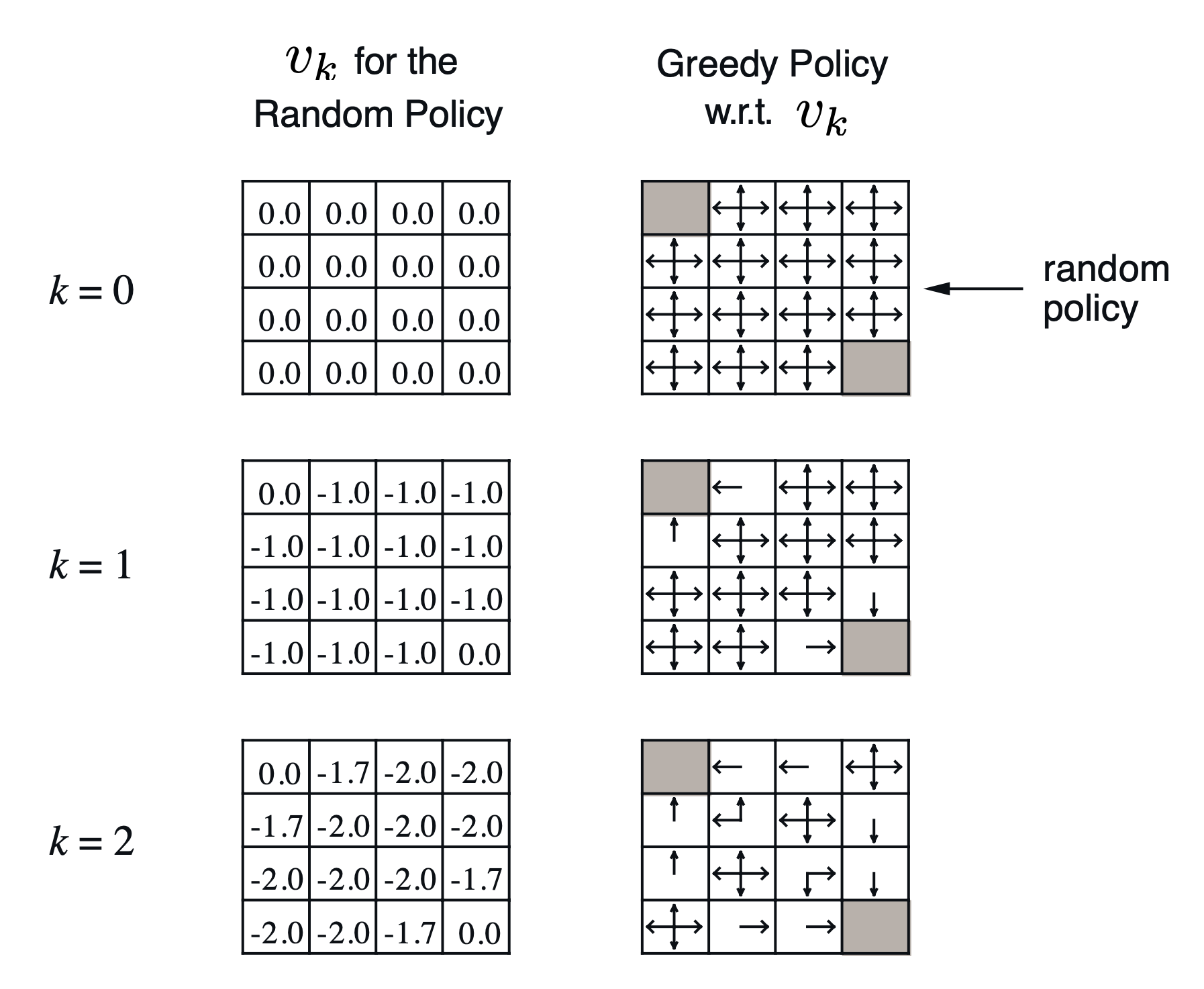

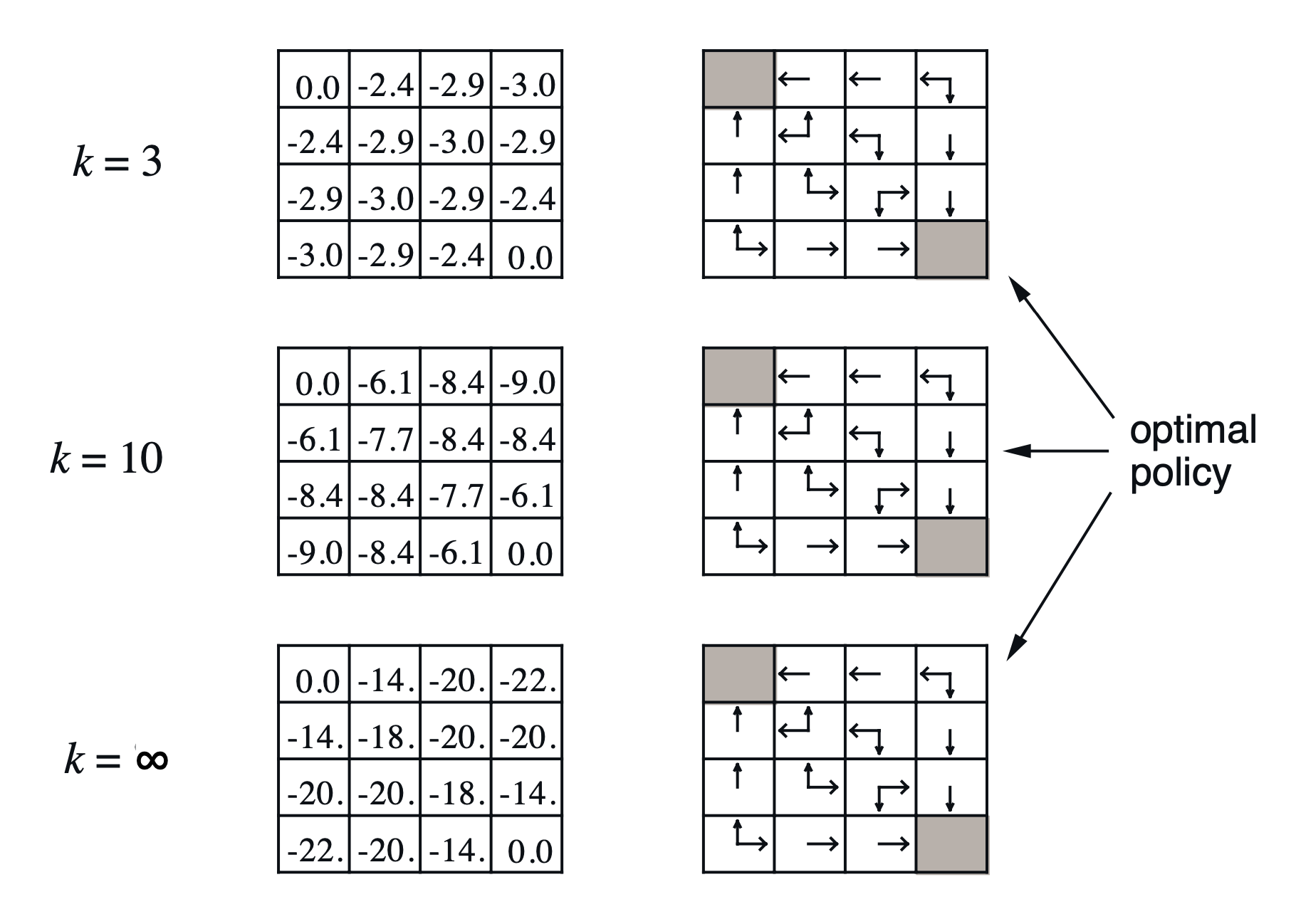
    $v_{1}(6) = \sum_{a\in \mathcal \{n, s, w, e\}} 0.25 \times \left( -1 + 1\times \sum_{s'\in \mathcal \{2, 5, 7, 10\}} \mathcal 1\times 0\right) = -1$

    

    

    🤖 (이 예시에서는) 멍청한 policy를 기반으로 value function의 값을 계산하였는데, 계산된 value function에 대하여 value가 $\max$가 되게하는 action만 항상 그리디하게 선택하는 policy를 따랐더니 optimal policy가 되었다!

    → 더 나은 policy를 찾을 수 있다. [policy 개선의 아이디어]
    

3. Policy Iteration

Iterative한 방법을 사용하여 policy기반으로 최적의 policy를 찾는 과정

---

3.1 Policy 개선의 원리

• Evaluate the policy (=policy evaluation)
  $v_\pi(s) = \mathbb [R_{t+1} + \gamma R_{t+2} + \cdots | S_t = s]$
• Improve the policy
  $\pi' = \text{greedy} (v_\pi)$
  ⇒ Evaluate와 Improve를 반복해서 수행하면 점점 policy가 optimal policy $\pi*$에 수렴하게 된다!
  

3.2 Policy Iteration

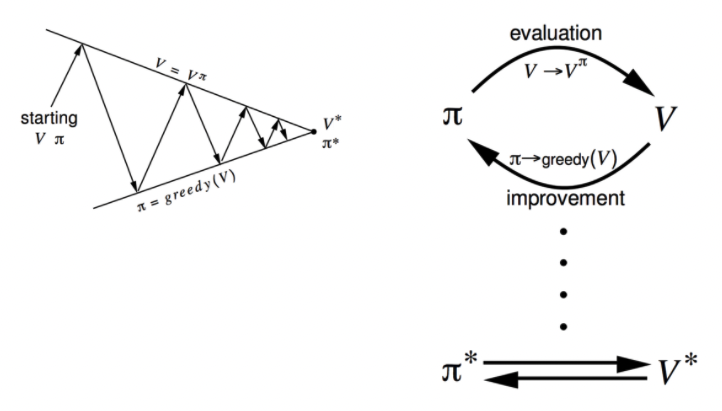
Policy 개선 과정

1. 초기 policy $\pi$를 평가 [evaluation]

2. 계산된 value function에 대하여 greedy하게 선택하는 새로운 policy $\pi'$로 policy를 개선 [improvement]

3. 개선된 policy $\pi'$를 다시 평가 [evaluation]

   $\cdots$

3.3 proof of policy Improvement

• $\text{Q}_1$. greedily하게 행동하는 새로운 policy는 항상 이전의 policy보다 개선되는가?

  • 어떤 deterministic$^{[1]}$한 policy, $a = \pi(s)$가 있다고 하자.

    [1] 어떤 state에서 어떤 action을 할 지 명확하게 정의된 policy → 확률 분포가 아님

  • greedily하게 행동하는 새로운 policy를 정의함으로서 우리는 policy를 improve시킬 수 있다

    $\pi'(s) = \arg\max_{a\in \mathcal A} q_{\pi} (s,a)$

  • one-step에 대한 policy improve 증명

    *notation

    $q_\pi(s, \pi(s))$ : $\pi$를 따라서 1-step을 수행하고 그 이후로도 계속 \pi를 따랐을 때의 action-value

    $q_\pi(s, \pi'(s))$ : $\pi'$를 따라서 1-step을 수행하고 그 이후에는 \pi를 따랐을 때의 action-value

    • $s$에서의 state-value는 $s$에서 policy에 의해 결정된 action $a = \pi(s)$을 수행했을 때의 action-value와 동일하다. (action-value function의 정의상 자명함)
    • policy가 결정한 action을 했을 때의 value는 value가 최대가 되도록하는 action을 했을 때의 value보다는 절대로 크지는 않을 것이다.
    • 그런데 greedily policy의 정의에 따라 이 값은 greedily policy에 의해 결정된 action $a= \pi'(s)$을 수행했을 때의 action-value와 동일하다.
      $q_{\pi} (s, \pi'(s)) = \max_{a\in\mathcal A} q_{\pi} (s,a) \ge q_{\pi} (s, \pi(s)) = v_\pi(s)$
      ⇒ one-step이라도 $\pi'$를 따라 진행했을 때의 action-value가 기존 policy를 따랐을 때의 value보다 항상 같거나 크다.
      

  • value function에 대한 증명

    • one-step일 때 증명한 것에 따라서 $v_\pi(s) ≤ q_\pi(s, \pi'(s))$이다. $-\ (1)$
    • Q-function의 정의에 의하여 아래와 같이 expectation 공식으로서 나타낼 수 있다.
      $v_\pi(s) \le q_\pi(s, \pi'(s)) = \mathbb E_{\pi'}[R_{t+1} + \gamma v_{\pi} (S_{t+1}) | S_t = s]$
    • one-step일 때 증명한 내용 (1)을 다시 적용하면 아래와 같이 표현할 수 있다.
      $\le \mathbb E_{\pi'} [R_{t+1} + \gamma q_\pi(S_{t+1}, \pi'(S_{t+1}))|S_t=s]$
    • Q-function에 대해 한번의 step을 더 진행하여 bellman equation처럼 재귀적으로 아래와 같이 표현할 수 있다.
      $\le \mathbb E_{\pi'} [R_{t+1} + \gamma R_{t+2}+\gamma^2 q_\pi(S_{t+2}, \pi'(S_{t+2}))|S_t=s]$
    • 재귀적인 과정을 반복하면 결국 value-function에 정의에 의하여 $v_\pi'(s)$로 표현된다.
      $\le \mathbb E_{\pi'} [R_{t+1} + \gamma R_{t+2}+\cdots |S_t=s] = v_{\pi'}(s)$
      ⇒ 따라서 모든 state에서 $\pi'$를 따랐을 때의 value가 $\pi$를 따랐을 때의 value보다 높기 때문에 policy는 항상 improvement 된다는 것을 보일 수 있다.

• $\text{Q}_2$. 개선된 policy는 최종적으로 optimal에 수렴하는가?
  • 아래 등식이 성립하는 상황이라면 어떤 policy에 수렴했다고 말할 수 있다.
    $q_{\pi} (s, \pi'(s)) = \max_{a\in\mathcal A} q_{\pi} (s,a) = q_{\pi} (s, \pi(s)) = v_\pi(s)$
  • bellman optimality equation을 적용할 수 있는 상황이다.
    • $v_\pi(s) = v_*(s)$ for all $s \in \mathcal S$
    • 따라서 $\pi$는 optimal policy이다.
      $v_\pi(s) = \max_{a\in \mathcal A} q_\pi(s, a)$

3.4 Modified Policy Iteration

💬 Q. policy iteration을 수행할 때, evaluation단계에서 $v_\pi$가 수렴할 때까지 반드시 진행해야하는가?

*여러가지 아이디어

• $\infin$보다 조금 더 일찍 종료할 수는 없을까?
• $k=3$과 같이 iteration횟수를 정해두고 수행하면 안될까?

A. $v_\pi$가 수렴할 때까지 진행하지 않아도 된다!

극단적인 경우, 단 한번만 policy evaluation을 진행하고 바로 policy improvement 단계로 넘어가도된다.

정확히 수렴하지는 않았지만 달라진 policy에 대한 value가 업데이트 되었기 때문!

4. Value Iteration

policy가 존재하지 않을 때 Iterative한 방법을 사용하여 value 기반으로 최적의 value function을 찾는 과정

---

4.1 Principle of Optimality : Theorem

• optimal policy의 component
  • 첫번째로 optimal action $A_*$를 수행한다.
  • 이후 그 다음 state $S'$에서 다시 optimal policy를 따라 진행한다.
• Principle of Optimality : Theorem

  A policy $\pi(a|s)$ achieves the optimal value from state $s$, $v_\pi(s) = v_*(s)$, if and only if

  • For any state $s'$ reachable from s
  • $\pi$ achieves the optimal value from state $s'$, $v_\pi(s') = v_*(s')$

4.2 Deterministic Value Iteration

• value iteration; DP의 도입
  • $v_*(s')$를 구하는 문제는 여러개의 subproblem들로 표현할 수 있다.
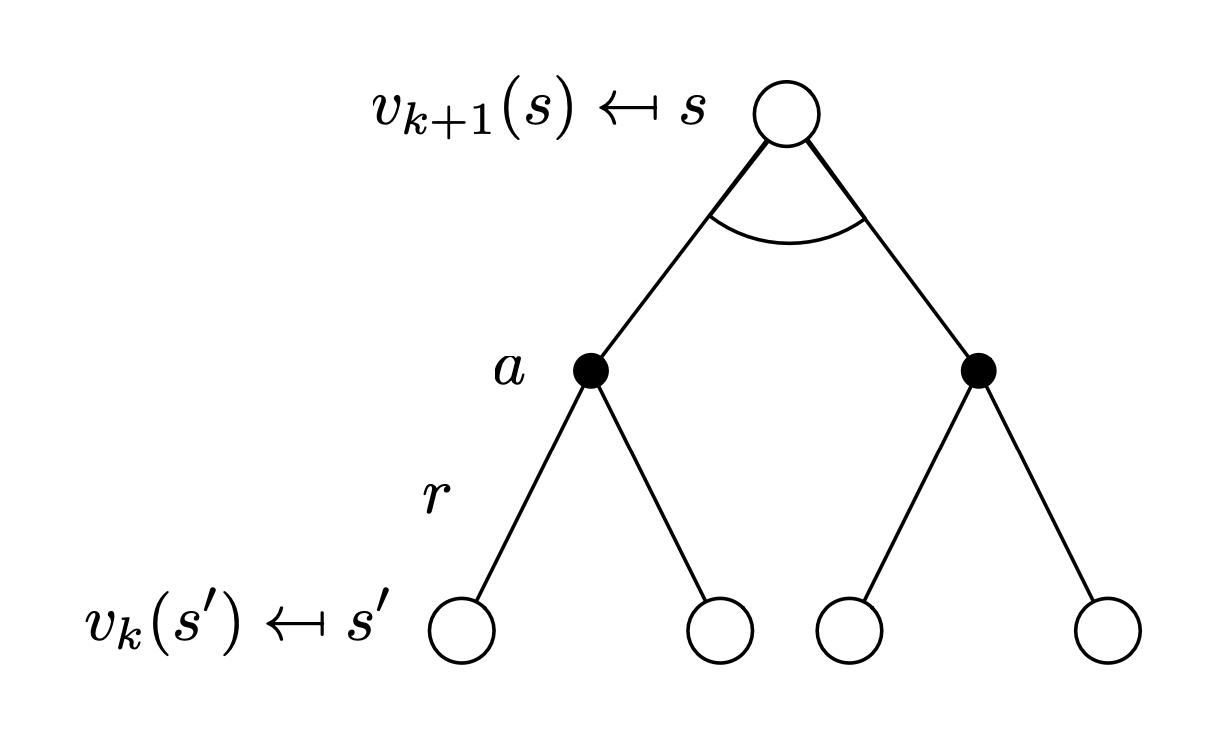
  • subproblem one-step lookahead를 통하여 $v_*(s)$를 구할 수 있다. [Bellman Optimality Equation]
    $v_*(s) \leftarrow \max_{a\in\mathcal A} \left(\mathcal R^a_s + \gamma \sum_{s' \in \mathcal S} \mathcal P^a_{ss'} v_*(s')\right)$

### 4.3 Example with Gridword

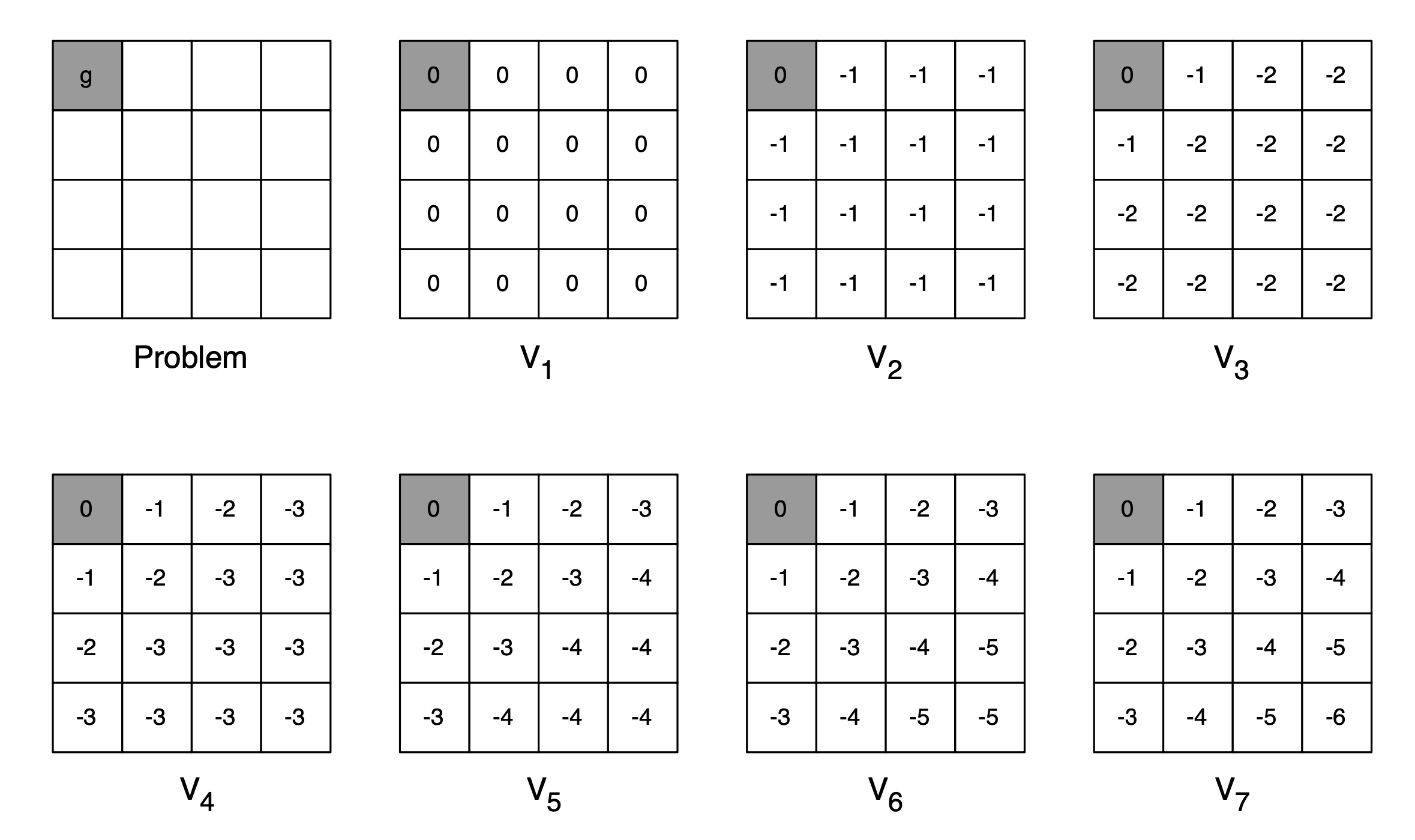
• 문제 : 최단거리를 찾는 문제

  • reward는 항상 -1

    

4.4 Value Iteration

• 문제 정의
  • problem : optimal policy $\pi$를 찾는 것을 목적으로 한다.
  • solution : Bellman optimality equation을 이용하여 iterative한 방법을 적용한다. $v_{1;\ init} → v_2 → \cdots → v_*$
    
  • synchronous backup

    1. each iteration k+1

       2. for all states $s \in \mathcal S$

          3. update $v_{k+1}(s)$ from $v_k (s')$

             → 전 단계 $k$에서의 value f를 이용하여 현재 단계 $k+1$에서의 value를 갱신한다.

             (where $s'$는 $s$에서 갈 수 있는 가능한 모든 state)

       → 이 과정을 반복하면 $v_\pi(s)$에 수렴하게 된다.

  • policy가 주어지지 않는다.

• Bellman optimality Equation

  

  $v_{k+1}(s) = \max_{a\in \mathcal A} \left( \mathcal R^a_s + \gamma \sum_{s'\in \mathcal S} \mathcal P^a_{ss'}v_k(s')\right)$
  $\bold v_{k+1} = \max_{a\in\mathcal A} \mathcal R^{\pi} + \gamma \mathcal P^\pi \bold v_k$

model을 알 때, prediction과 control문제의 해결방법

문제	사용하는 벨만 방정식	알고리즘
Prediction	Bellman Expectation Equation	Iterative
Policy Evaluation
Control	Bellman Expectation Equation +
Greedy Policy Improvement	Policy Iteration
Control	Bellman Optimality Equation	Value Iteration

5. Extensions to DP*

기본적인 DP 방법을 적용하여 RL문제를 해결하는 것은 computation적으로 비효율이 너무 크기 때문에 여러가지 테크닉을 이용한다.

---

5.1 Asynchronous DP

• In-Place DP

  • 기존 방법 (synchronous) : $k$번째의 value function에 대한 정보와 $k+1$번째의 value function에 대한 정보를 따로 저장해야하기 때문에 2배의 저장공간을 필요로 한다.
    $v_{\text {new}}(s) \leftarrow \max_{a\in \mathcal A} \left( \mathcal R^a_s + \gamma \sum_{s'\in\mathcal S} \mathcal P^a_{ss'} v_{\text{old}}(s')\right)\\\ \\ v_{\text{old}} \leftarrow v_{\text{new}}$
  • In-Place : 갱신된 값과 갱신되지 않은 값을 저장하기 위한 공간을 따로 할당하지 않고 바로 덮어씌워서 업데이트 한다.

    • 다른 state에 대해 value를 계산할 때는 이제 바로 직전에 갱신된 값을 사용하게된다.

    • 이렇게 구현하더라도 문제를 풀 수 있다는 것은 증명되어있다.

      $v(s) \leftarrow \max_{a\in \mathcal A} \left( \mathcal R^a_s + \gamma \sum_{s'\in\mathcal S} \mathcal P^a_{ss'} v(s')\right)$

• Prioritised Sweeping

  • state에 우선순위(priority)를 두어, value를 업데이트할 때 중요한 state를 먼저 갱신한다.

  • 중요한 state?
    → Bellman error가 큰 state

    $\left| \max_{a\in \mathcal A} \left( \mathcal R^a_s + \gamma \sum _{s' \in \mathcal S}\mathcal P^a_{ss'}v(s') \right) - v(s)\right|$

• Real-Time DP

  • state의 공간은 매우큰데 실제로 agent가 유의미하게 자주 방문하는 state는 그리 많지 않을 때,
  • Agent가 실제로 방문한 state를 먼저 업데이트한다.

---

5.2 Full-width & sample backups

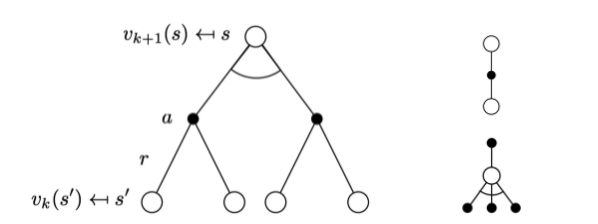
• Full-width backup
  • DP의 방법론
  • $s$에서 갈 수 있는 모든 $s'$를 이용하여 업데이트한다. → 이럴 필요가 있는가?

• Sample backup

  • large MDP에서는 Full-width backup으로 구현하기 매우 어렵다.

    (state수가 늘어날 수록 계산량이 exponential하게 변화함)
    

  • Advantage

    • state가 많아지더라도 고정된 sample의 수만 확인하기 때문에 cost가 일정하다.
    • Model-free인 문제에서도 수행할 수 있다.
    • break the curse of dimensionality

    

5.3 Approximate DP

Reference

• Introduction to Reinforcement Learning by David Silver
• 팡요랩 : 강화학습의 기초 이론