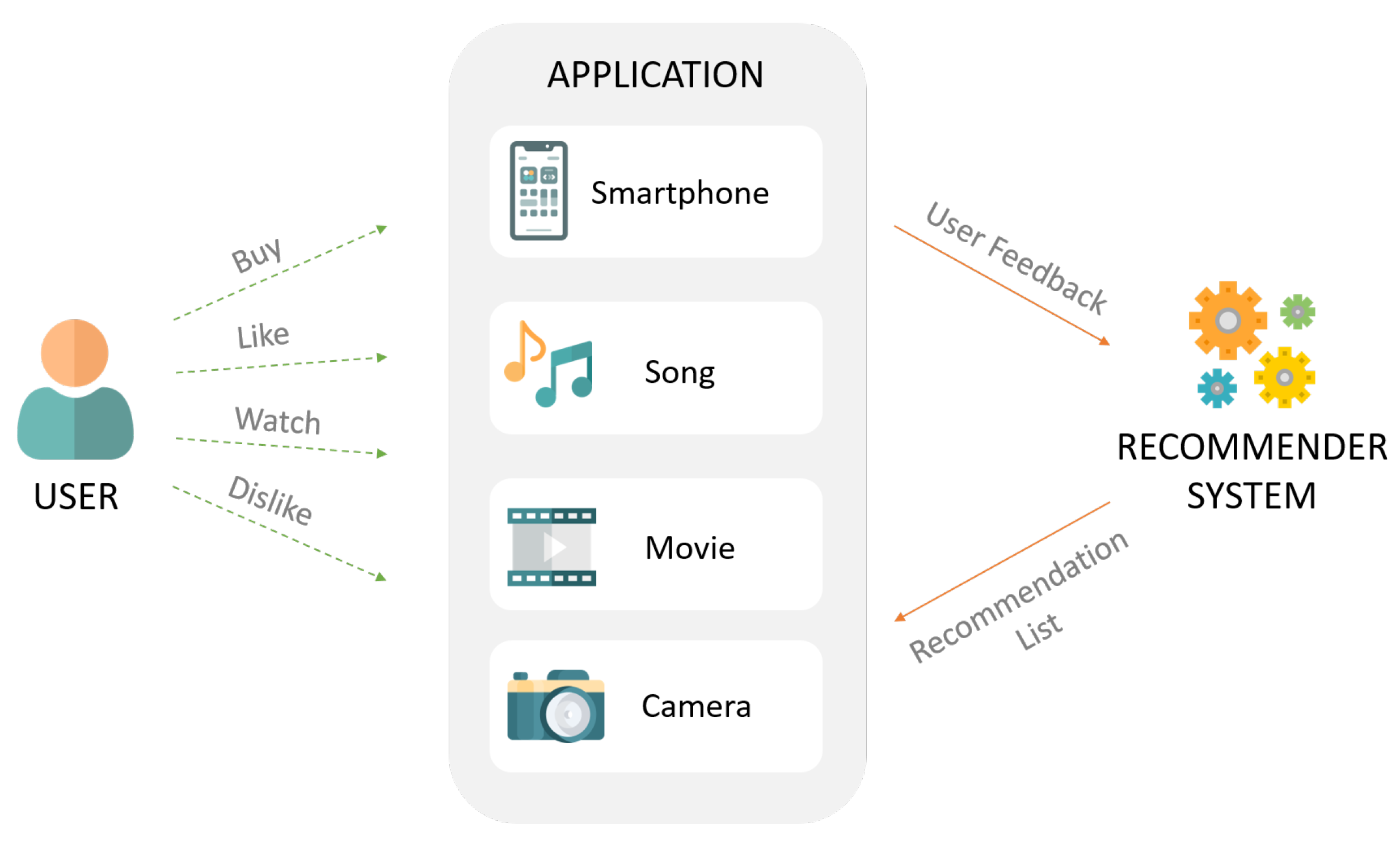
Intro
최근 협업 필터링에 딥러닝을 적용한 많은 모델들이 좋은 성능을 보여왔습니다. 그러나 컴퓨터비전과 같은 분야와는 다르게 적은 은닉층을 가진 모델이 최고의 추천 정확도를 달성하고 있습니다. (따라서) 이 논문에서 우리는 더 극단적으로 은닉층이 없는 선형 모델을 정의합니다.
입력 벡터는 사용자가 상호작용한 아이템을 나타내며, 모델의 목표(출력에서)는 사용자에게 추천할 최고의 아이템을 예측하는 것입니다. 이 모델은 autoencoder처럼 입력을 출력으로 복원시키는 과정을 통해 수행됩니다. 따라서 우리는 이를 'Embarrassingly Shallow Autoencoders'라고 이름지었습니다.
Model Definition
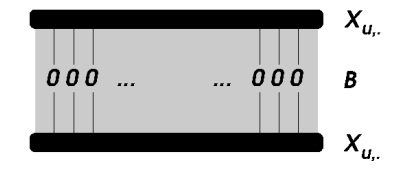
- : 유저 수
- : 아이템 수
- : 유저*아이템 크기의 상호작용 행렬(input data)
- sparse, binary(implcit data)
- 상호작용 -> 1, 상호작용하지 않음 -> 0으로 표기
- : 아이템*아이템 크기의 가중치 행렬
- 모델의 parameter
- 이때 가중치 행렬의 는 0으로 제한됩니다(항등행렬 가 되는 것을 방지(slim논문에서 나왔었던 방법)).
- : 아이템 j가 유저 u에게 주어졌을 때의 predicted score
Model Training
가중치 행렬 를 학습시키기 위한 목적식은 다음과 같습니다.
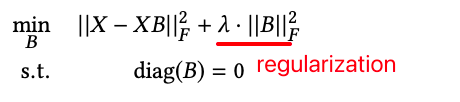
- 목적식으로 square loss를 사용한 이유는 Closed-form solution을 허용하기 떄문입니다.
- : Frobenius norm (vector의 L2 norm을 matrix로 확장한 것(참고))
- : 모델에 사용되는 유일한 하이퍼파라미터입니다.
Closed-Form Solution
Model Training의 목적식은 Closed-Form으로 풀 수 있습니다.
- (제약조건이 포함되어 있는 Optimization 문제를 해결하기 위해) 라그랑주 승수법(Lagrangian multipliers)을 통해 제약조건()을 목적식(min)에 적용합니다.
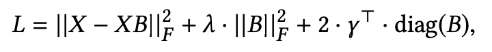
- 이때, = 는 Lagrangian multipliers의 vector입니다.
- (위에서 말한) 제약조건이 포함된 Optimization 문제는 Lagrangian을 최소화함으로써 해결할 수 있는데, 이에 대한 필요조건으로서 우리는 도함수를 0으로 설정(==의 도함수를 0으로 만드는 를 찾는 것) 하여 항을 재배열한 뒤 가중치 행렬의 추정값 을 산출합니다
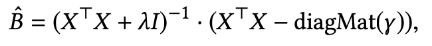
- 이때, 는 대각행렬과 단위행렬 를 의미합니다.
- 공식()의 앞 부분(()을 로 두고 방정식을 다시 정의하면, 다음과 같이 나옵니다.
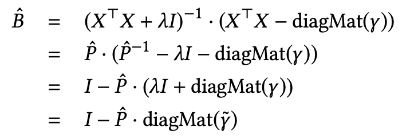
- 마지막 줄에 vector 는 로 정의됩니다.
- 은 1의 벡터를 의미합니다.
- Lagrangian mulipliers 값인 는 다음과 같이 이라는 제약에 의해 결정됩니다.
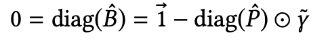
- 위 식에서 는 elementwise product이고, 에 대해 다시 정리하면 다음과 같습니다.
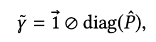
- 는 원소들의 나눗셈을 의미합니다.
- 이것들을 다시 정리하여 공식에 대입하면 다음과 같이 (Closed-Form으로)정의됩니다.
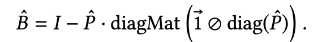
- 마지막 줄에 vector 는 로 정의됩니다.
- 즉, 결과적으로 학습되는 가중치는 다음과 같습니다.
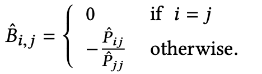
- i==j일 땐(diag matrix), 0으로 나오며, 그 외에는 모두 를 통해 나타낼 수 있습니다.
- 는 앞서 구한 바와 같이 (를 통해 구할 수 있습니다.
- i==j일 땐(diag matrix), 0으로 나오며, 그 외에는 모두 를 통해 나타낼 수 있습니다.
위 계산식을 보면, 가 결국 Gram-matrix (= 아이템-아이템 행렬)에 의해 계산된다는 것을 보여줍니다. 이는 앞선 살펴보았던 목적식에서 square loss를 사용한 결과이며, sparse한 데이터 X에서 를 계산하는 데 도움이 됩니다.
- 는 co-occurrence matrix를 의미합니다.
❗️co-occurence matrix란? (참고한 자료)
다음과 같이 interaction()이 있다고 가정합시다.
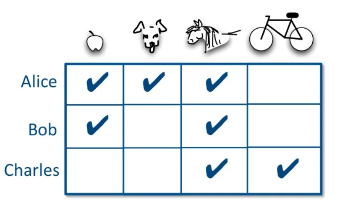
이를 co-occurrence matrix()로 표현하면(자기자신은 제외), 다음과 같습니다.
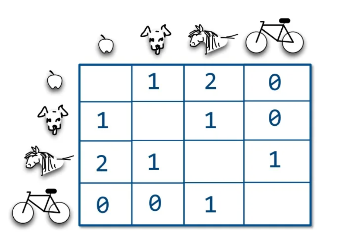
첫 번째 행을 살펴보면, '사과'가 선택됐을 때 강아지, 말, 자전거가 선택되는 빈도를 알 수 있습니다.
-> 대부분의 Neighborhood-based 접근법과 유사! (뒤에서 EASE와 비교하여 더 다룰 예정입니다.) - co-occurrence인 의 불확실성은 (대략적으로)포아송 분포(poisson distribution)의 표준편차 에 의해 결정됩니다. 이때 co-occurrence counts가 충분히 크다면, 와 는 작은 에러로 추정될 수 있습니다.
- 여기서 흥미로운 사실은 의 entry가 다음과 같은 두 가지 요인에 의해 증가된다는 것입니다.
- 유저의 활동량이 증가하여 데이터 의 밀도가 더 높아진 경우
- 데이터 의 유저 수가 증가할 경우
- (2)번의 의미를 생각해보면, 의 sparsity가 커져도, 유저의 수가 커지게되면 이를 보완할 수 있습니다. 다시 말해, 유저별로 활동량이 많지 않은 sparse한 데이터 하더라도 유저 수가 충분히 많다면, 를 추정하는 것의 불확실성에는 영향을 주지 않는다는 것입니다.
- 따라서 (논문 제목에서도 말하고 있듯이) 'Sparse한 데이터에 대해 강점이 있다' 이라고 말할 수 있습니다.
Algorithm

EASE의 학습은 가 아니라 (=)가 입력으로 들어가기 때문에, 의 크기( X )보다 의 크기( X )가 더 작을 경우 특히 효율적입니다. 즉, 아이템 수에 비해 유저 수가 많을 경우에 매우 효율적입니다.
- 그러나 이는 (반대로 말하면) 아이템 수가 유저 수보다 상대적으로 많다면, 효율적이지 않을 수 있다는 것을 의미하기도 합니다.
Comparison with Neighborhood-based Approaches
본 논문을 통해 저자는 EASE의 closed-form solution은 기존 neighborhood-based 접근이 개념적으로 잘못되었음을 보여준다고 말하고 있습니다.
- 대부분의 neighborhood-based 접근법에서는 co-occurrence matrix(Gram-matrix, )를 사용합니다.
- 그러나 EASE 모델에서 solution을 구해보니, 이러한 co-occurrence matrix를 그대로 사용하는 것이 아니라, 이를 inverse한 행렬을 사용하는 것이 더 정확한 방법이였다고 말하고 말하고 있습니다.
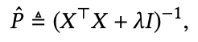
- 또한, 다른 (높은 성능을 보이는)모델들과 비교하여 우수한 성능을 보이고 있는 EASE가 원칙적인 neighborhood approach라고 볼 수 있다고 말하고 있습니다.
