1. Graph
1-1. Graph란?
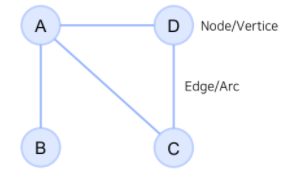
- 그래프(Graph)란, 꼭지점(Node)들과 그 노드를 잇는 변(간선, Edge)들을 모아 구성한 자료구조를 의미합니다.
- 간선 타입의 종류는 다음과 같이 나눌 수 있습니다.
- 간선에 방향이 있는가?
-> directed / undirected - 간선에 가중치가 있는가?
-> weighted / unweighted
- 간선에 방향이 있는가?
그래프 표시 예시 (상단 그림)
-> G = ({A,B,C,D}, {{A,B},{A,C},{A,D},{C,D}})
<Graph를 사용하는 이유>
- 관계, 상호작용과 같은 추상적인 개념을 다루기에 적합합니다.
- 복잡한 문제를 더 간단한 표현으로 단순화할 수 있습니다.
- 소셜 네트워크, 바이러스 확산, 유저-아이템 소비 관계 등을 모델링할 수 있습니다.
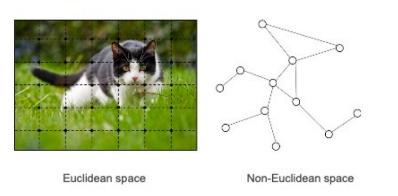
- Non-Euclidean Space의 표현 및 학습이 가능합니다.
- 우리가 흔히 다루는 이미지, 텍스트, 정형 데이터는 격자 형태로 표현 가능하지만,
- SNS 데이터, 분자(molecule) 데이터 등은 이가 불가능하므로 Non-Euclidean Space로 표현해야 합니다.
1-2. 그래프의 표현
Adjacency matrix(인접행렬)
-
Undirected
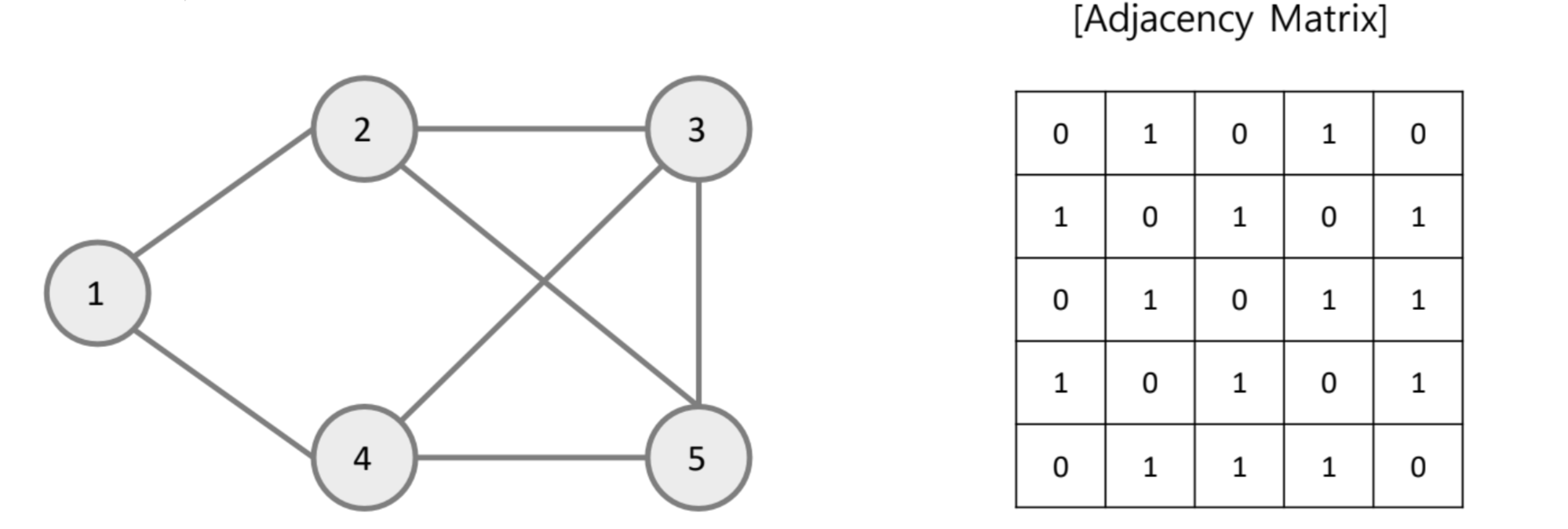
- Symmetric(대칭) 형태
-
Directed
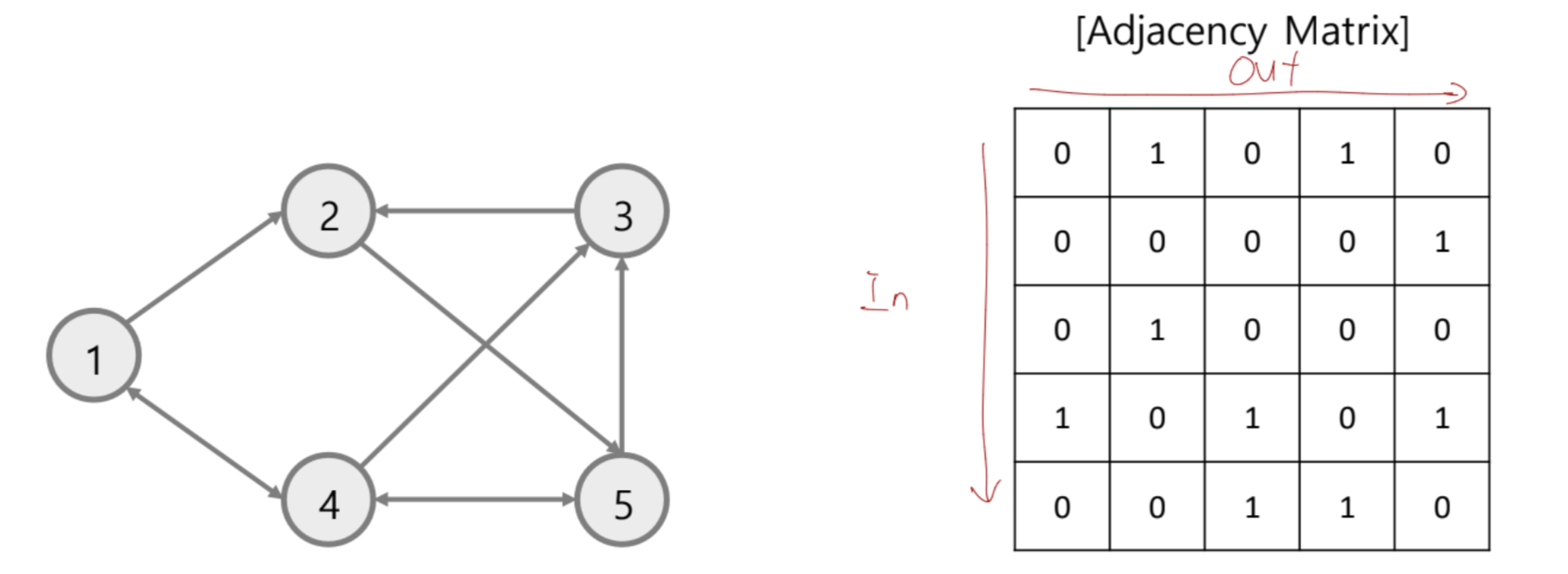
- Asymmetric(비대칭) 형태
-
Directed + Self-Loop
(Adjacency matrix + Identity matrix(항등행렬))
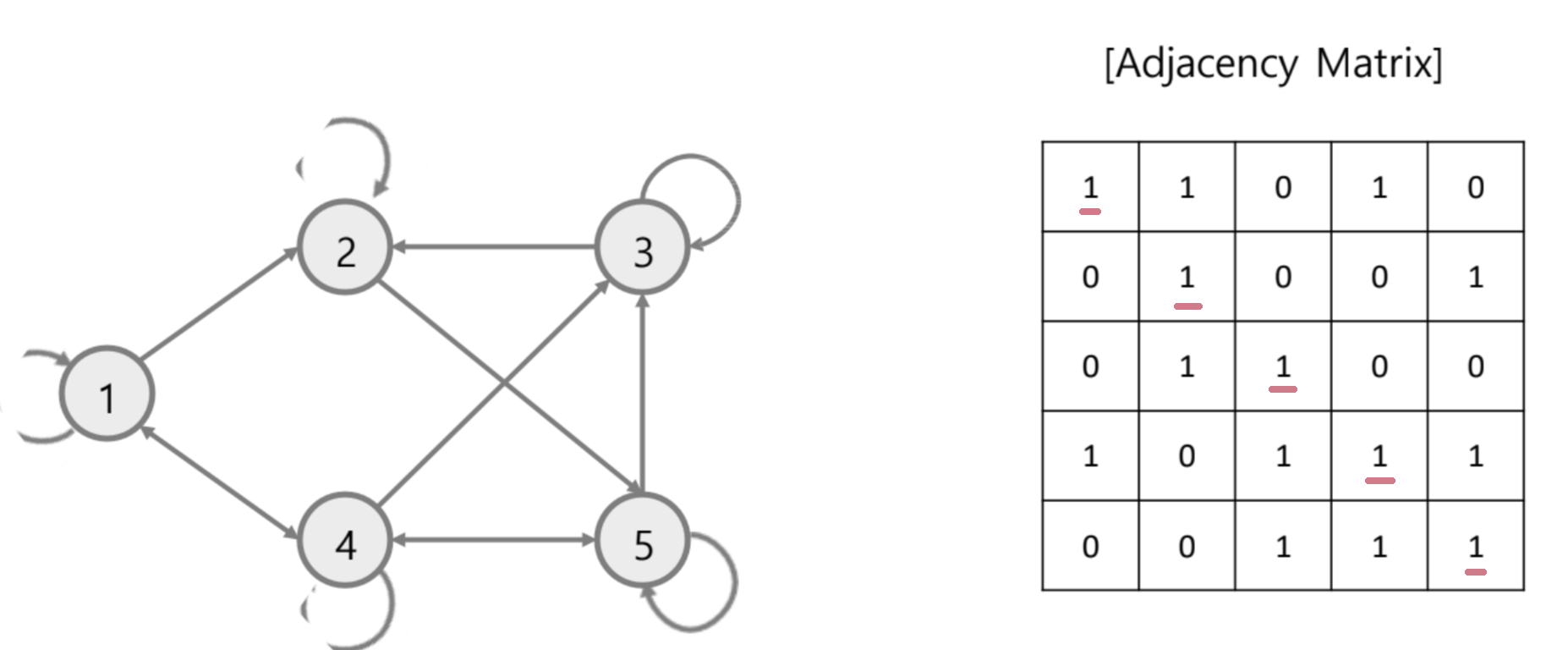
-
Weighted directed
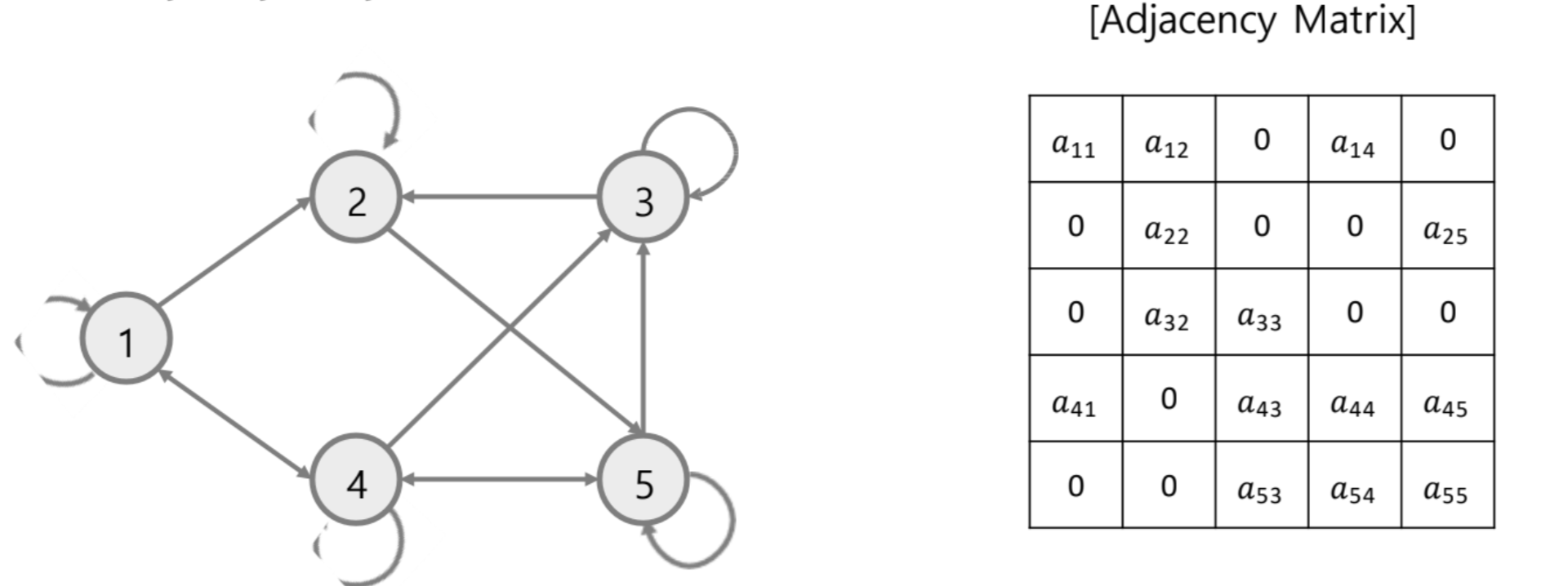
- Edge information이 있음
Degree matrix
: 각 노드가 주변과 몇 개나 연결되어 있는지를 표현해놓은 matrix
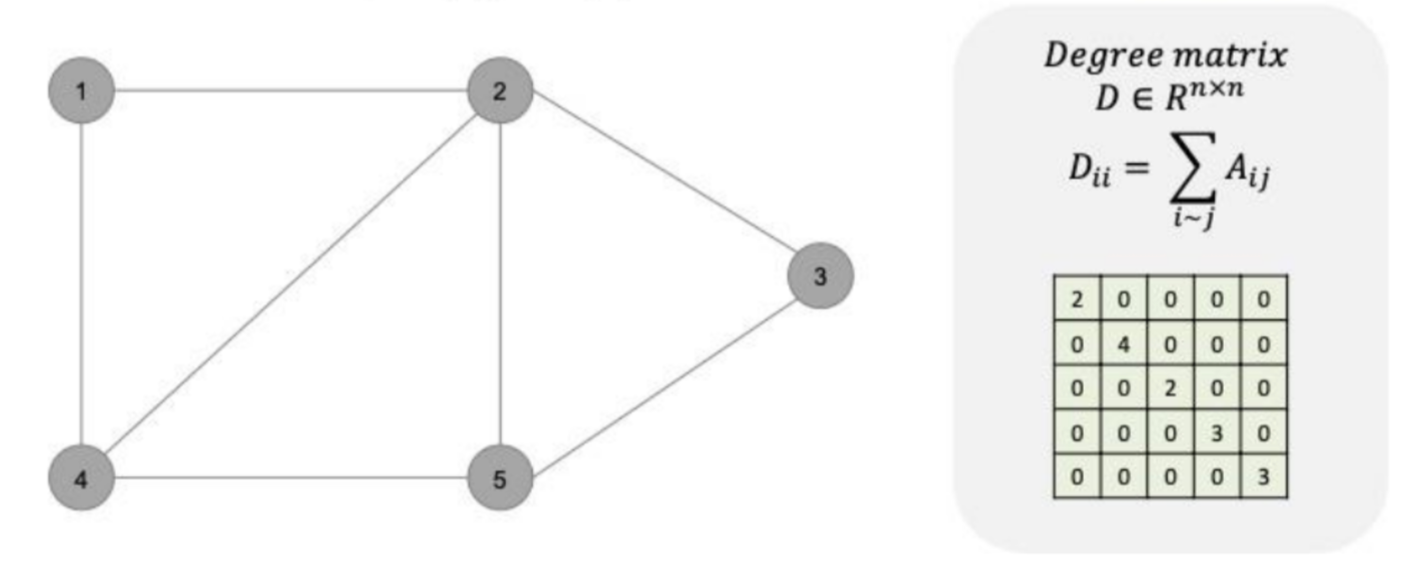
Laplacian matrix
: degree matrix에서 adjacency matrix를 뺀 matrix
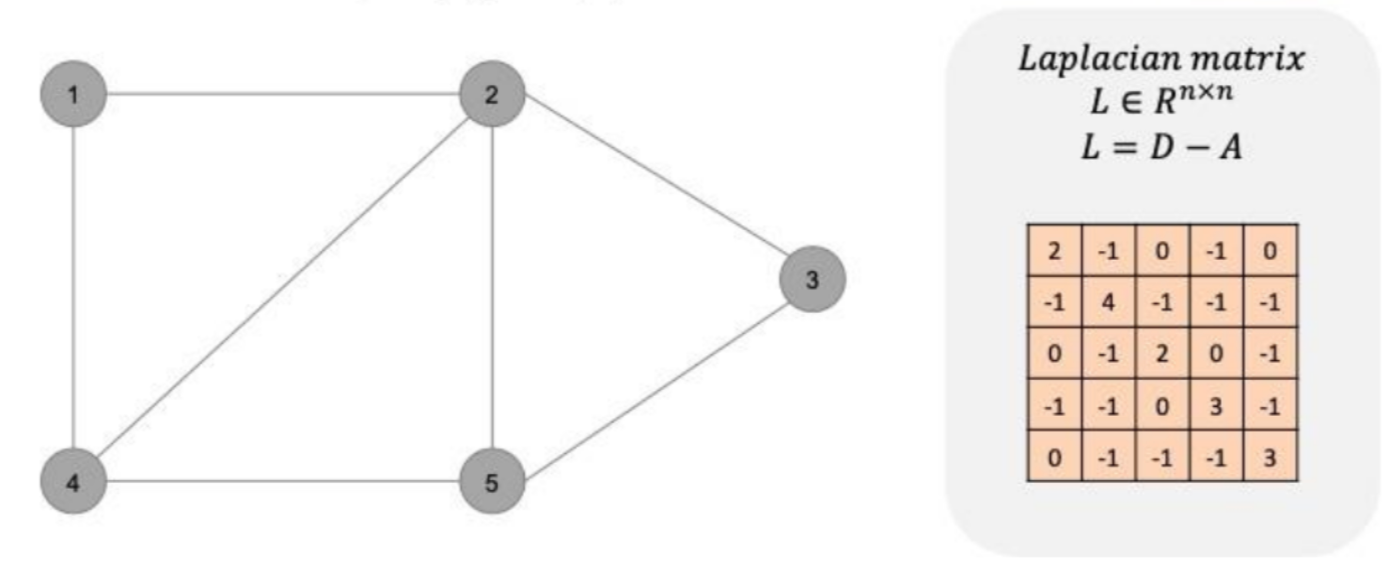
Node-feature matrix
: 각 노드에 hidden representation이 있을 때, 그것들을 모아놓은 matrix
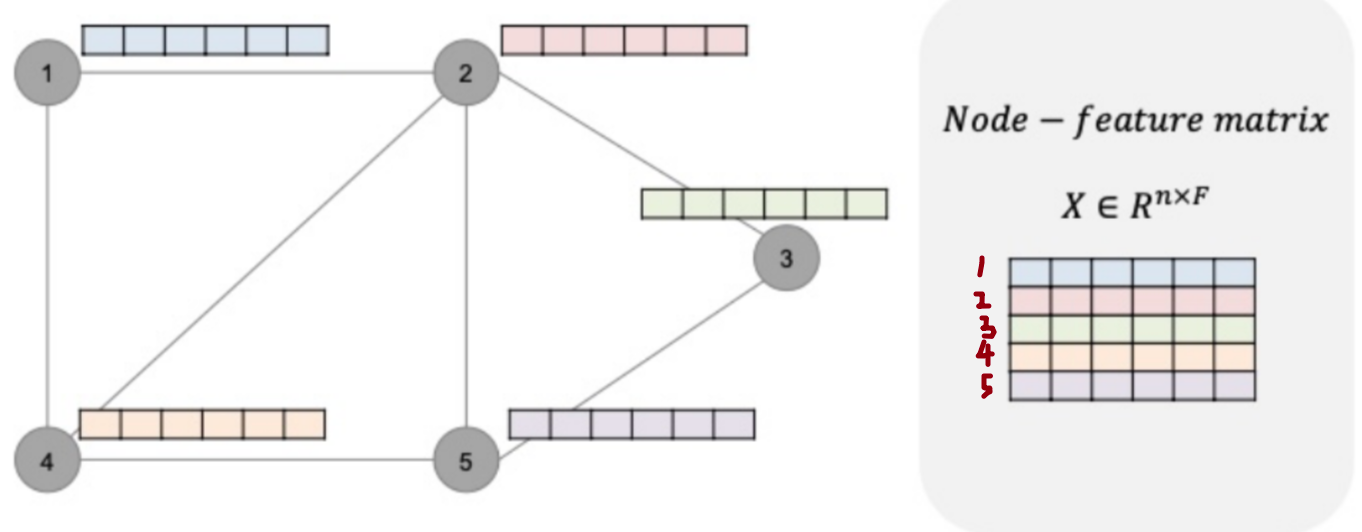
2. GNN
2-1. GNN이란?
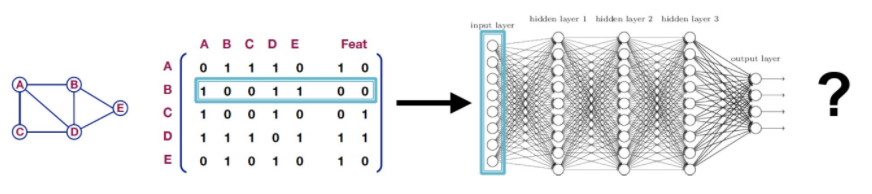
- GNN(Graph Neural Network)이란, 그래프로 표현할 수 있는 데이터를 처리하기 위한 인공 신공망의 한 종류입니다.
- CNN은 이미지에서 특징을 추출하여 어떠한 벡터를 만들고, 이를 통해 목적에 맞는 Task를 수행합니다.
- LSTM은 시계열 데이터에서 특징을 추출하여 어떠한 벡터를 만들어내고, 이를 통해 목적에 맞는 Task를 수행합니다.
- GNN 또한, 그래프 구조를 활용하여 특징을 추출하고 이를 통해 목적에 맞는 Task를 수행합니다.
- GNN을 통해 우리는 각 노드를 잘 표현할 수 있는 임베딩 추출(Efficient node embedding)을 기대할 수 있습니다.
- GNN은 그래프 구조를 활용하여 loss를 최적화시키는 과정이라고 할 수 있습니다.
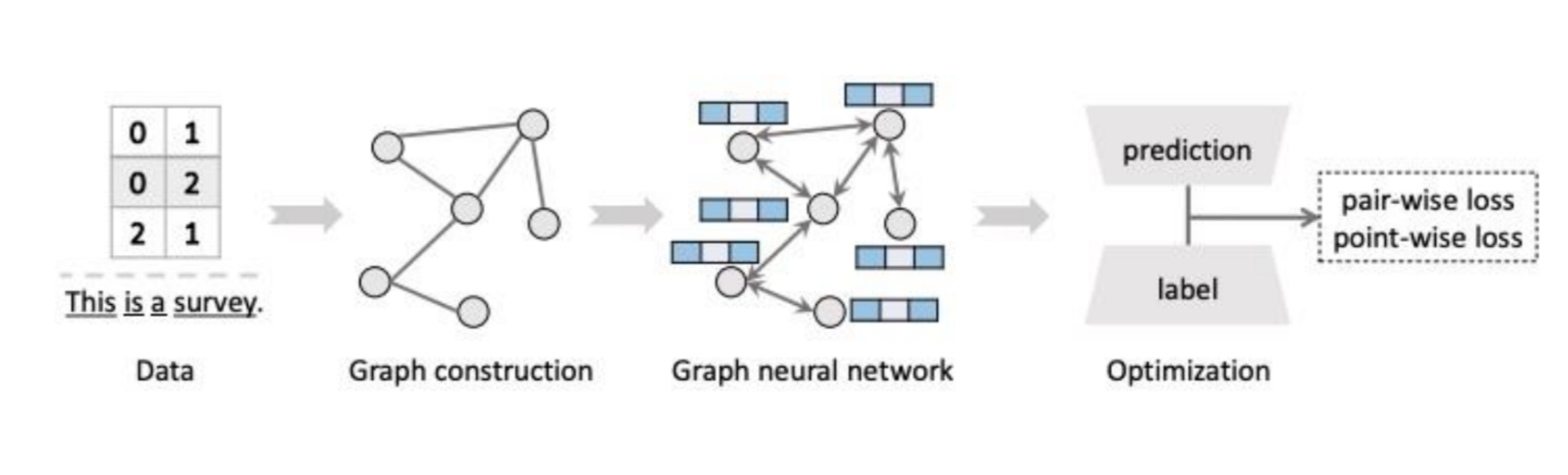
- GNN은 그래프 구조를 활용하여 loss를 최적화시키는 과정이라고 할 수 있습니다.
2-2. GNN 방법론
-
GNN은 크게 Spectral한 방법과 Spatial한 방법으로 나눌 수 있습니다.
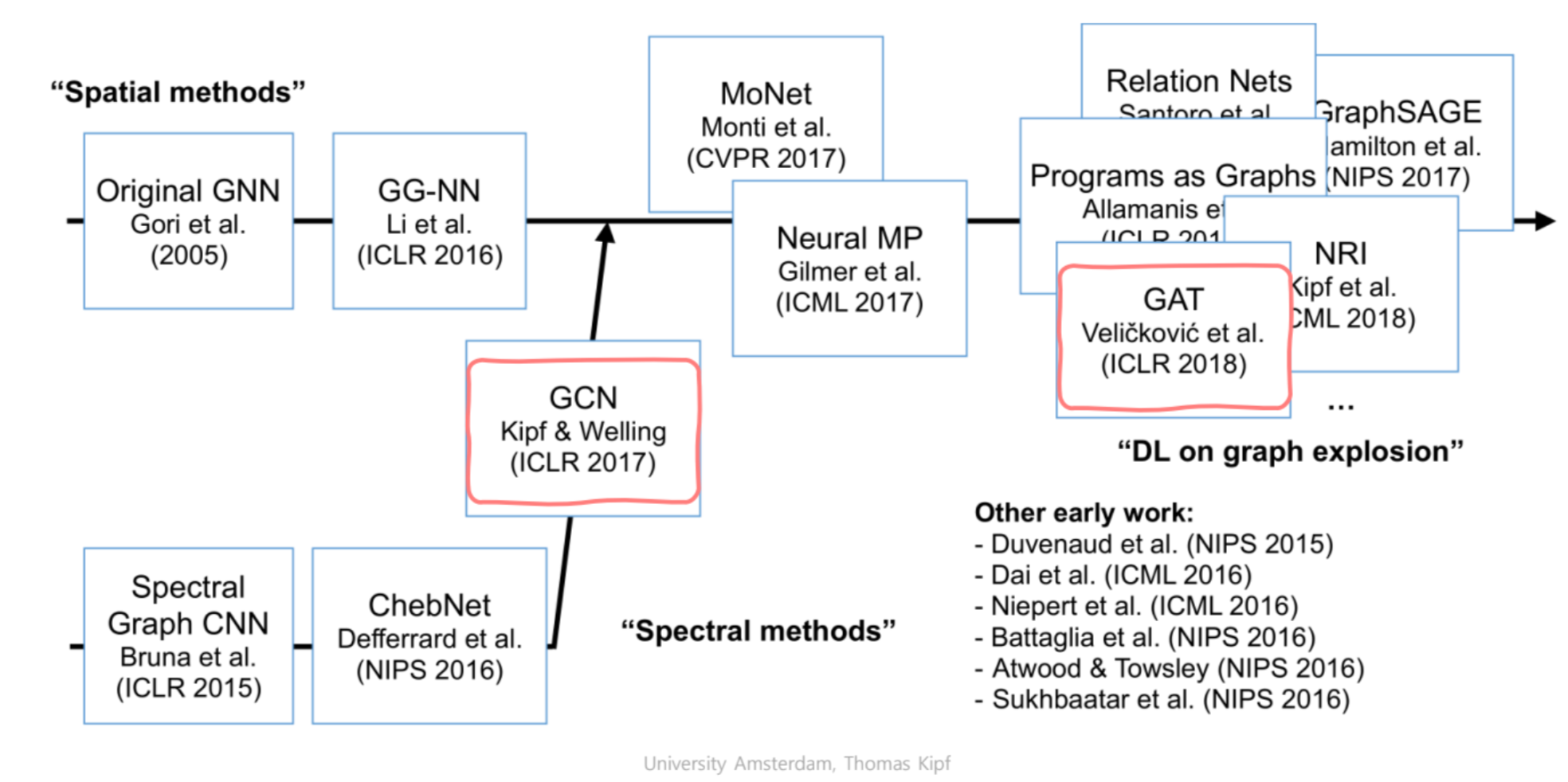
- 발전 과정을 살펴보면, 초기에는 Spectral한 방법으로 접근하였지만 현재에는 대부분 Spatial한 방법론들을 사용하고 있는 것을 알 수 있습니다.
- 그림을 보면 알 수 있듯, GCN은 Spectral -> Spatial 로 연결해주었던 아키텍처입니다. GCN 등장 이후 Spatial 방법론의 연구가 주를 이루게 됩니다.
- Spatial Methods는 Neighborhood aggregation으로 간단히 표현할 수 있습니다. 즉, 어떠한 Target Node의 주변 정보를 가지고 자기 자신을 업데이트하는 방식입니다.
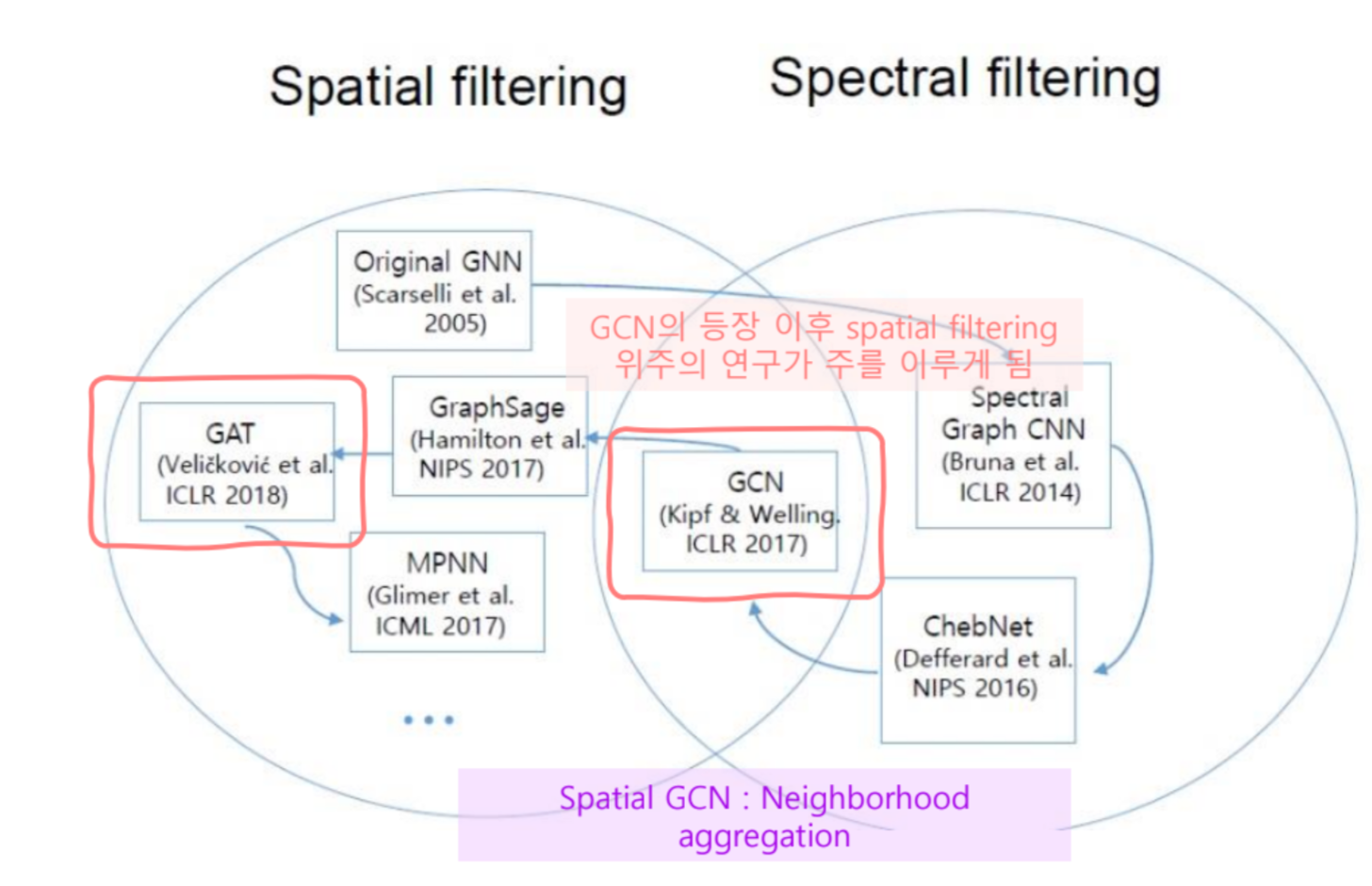
- 발전 과정을 살펴보면, 초기에는 Spectral한 방법으로 접근하였지만 현재에는 대부분 Spatial한 방법론들을 사용하고 있는 것을 알 수 있습니다.
-
이제 Spectral -> Saptial의 다리 역할을 하였던 GCN과 Spatial의 대표적인 연구인 GAT의 방법들을 간단히 살펴보면서 GNN을 이해해보도록 하겠습니다.
2-3. GCN(Graph Convolutional Networks)를 통해 GNN 이해하기
Euclidean vs Non-euclidean
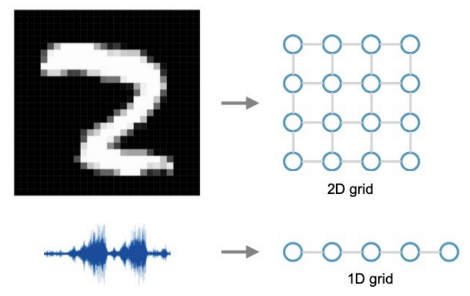
- 우리가 흔히 다루는 이미지, 텍스트, 정형 데이터는 격자 형태로 표현이 가능합니다. 즉, 유클리디언 공간 상의 격자 형태로 표현할 수 있습니다.
- 유클리디언 공간에서는 '거리'가 중요합니다.
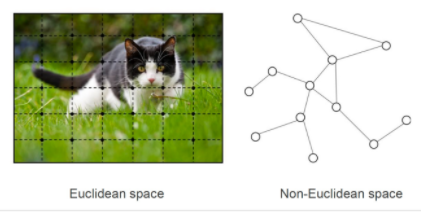
- 유클리디언 공간에서는 '거리'가 중요합니다.
- 반면, 소셜 네트워크와 분자 데이터 등은 유클리디언 공간으로 표현할 수 없습니다.
- 유클리디언 공간이 아니므로 거리가 중요하지 않으며, '연결 여부'와 '연결 강도'가 중요합니다.
Convolution (on Graphs)
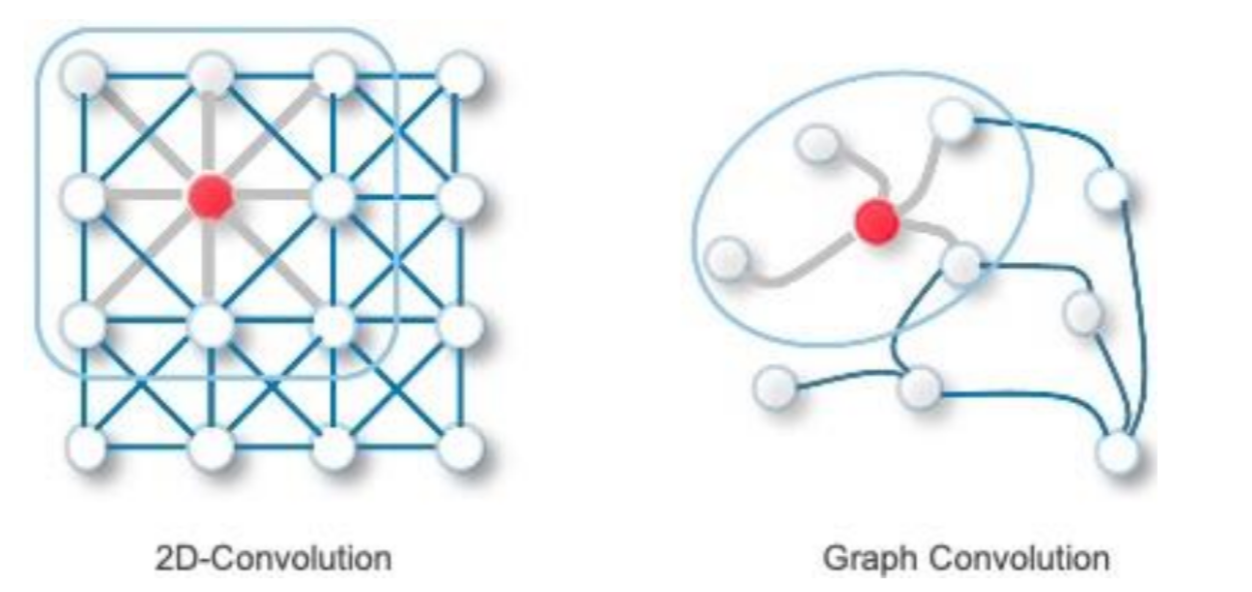
- CNN에서 사용되는 Convolution은 결국 커널을 움직여가며 커널 크기에 해당하는 정보들을 한 곳에 모으는 과정이라고 할 수 있습니다.
- Graph에서는 (Target)노드와 연결된 이웃들의 정보를 weighted average함으로써 Convolution 효과를 만들어냅니다.
가중치 업데이트 과정
가중치 업데이트 계산
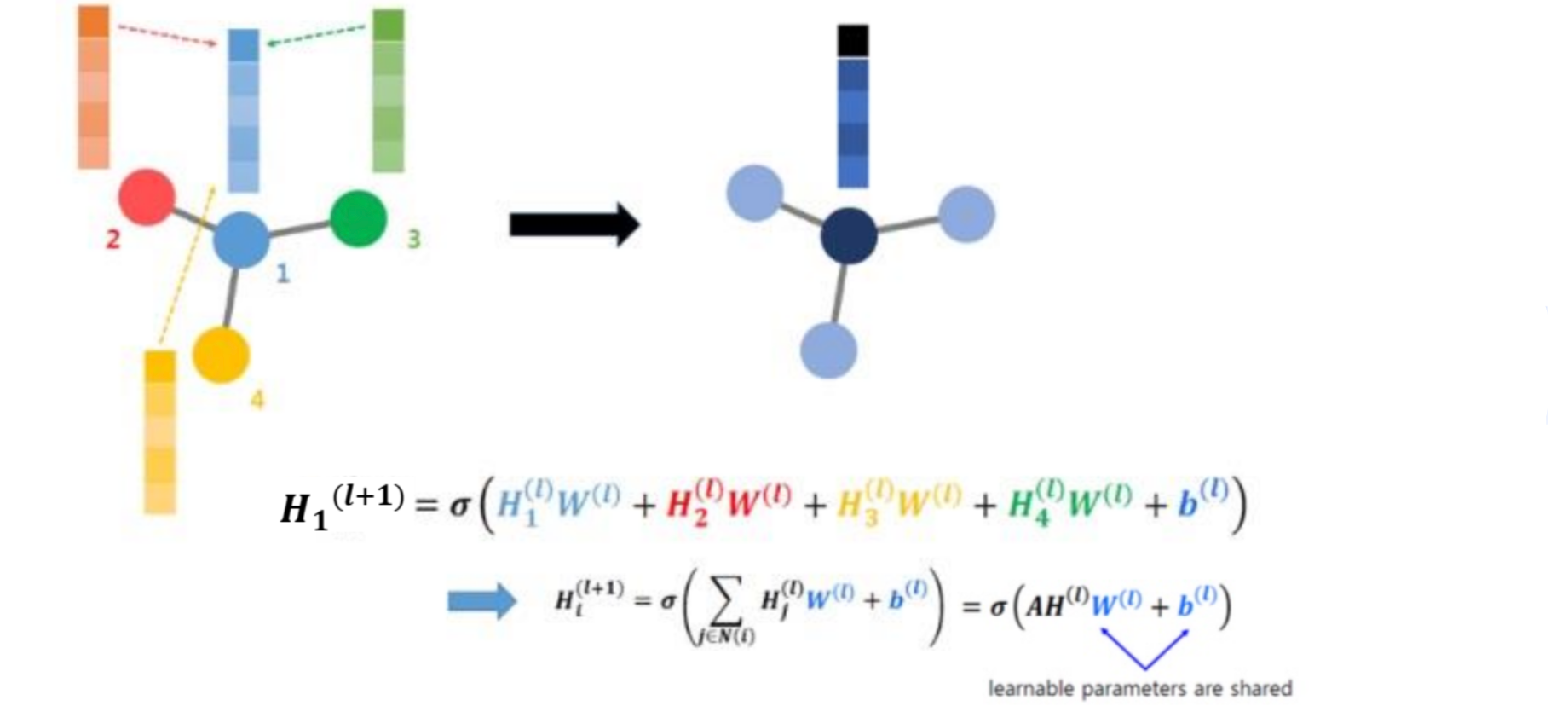
- Target node(그림에서 1번)의 주변 노드에 대한 정보를 학습합니다.
- 각 벡터 값에 파라미터를 곱하고, 이를 모두 더함(Convolution 효과)
- 는 Adj matrix 를 의미
- 이때, 학습되는 파라미터()는 공유됩니다.
GCN은 결국,
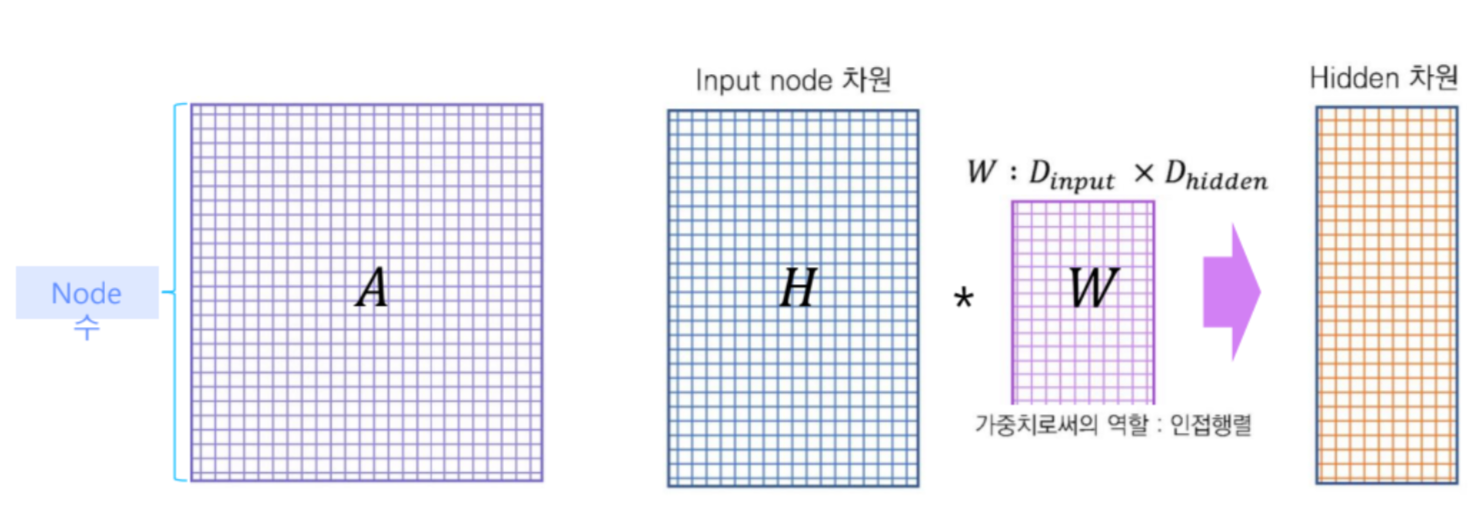
- 위 과정을 통해 계산되어진 output은 1번 업데이트된 임베딩이 될 것입니다.
- Shape
- :
- :
- :
- output:
가중치 계산에서의 한계점과 해결책
- 인접행렬 는 주변 노드(Neightbor node)와의 연결만 표시하기 때문에 자기 자신의 정보는 날아가게 됩니다. 따라서 항등행렬을 이용하여 자기 자신을 추가로 고려해줄 수 있습니다.
- (self-loop)
- 에서 노드는 각 연결 수가 천차만별이므로(정규화 되지 않음), 연산 시 feature vector의 크기가 불안정할 수 있습니다. 정규화시킴으로써(각 degree만큼 나눠줌) 이를 해결할 수 있습니다.
(Spectral 방법론에서 사용되던 기법입니다.)- =
- 는 행렬을 사용하므로, 상호작용이 없는 유저-아이템에 대해서는 사용할 수 없습니다(Transductive).
2-4. GAT(Graph Attention Networks)를 통해 GNN 이해하기
GCN vs GNN
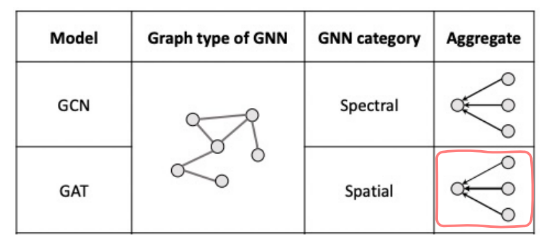
- GAT는 Spatial한 방법론을 사용합니다. 따라서 Adj Matrix를 사용하지 않습니다.
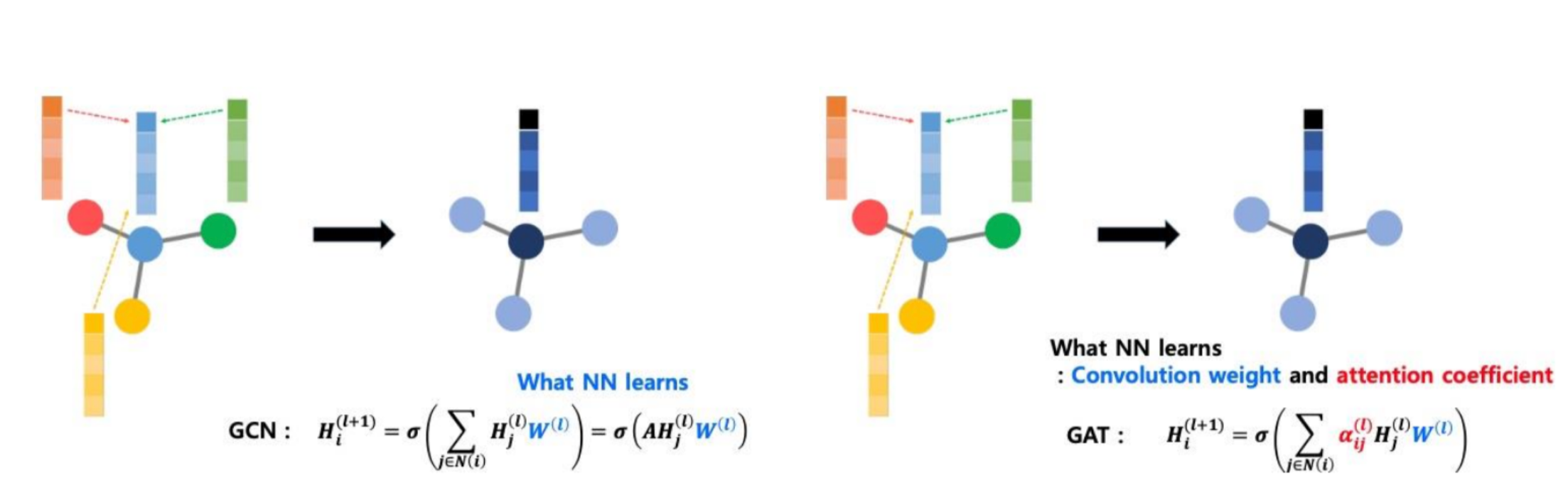
- GAT는 단순히 합치는 것이 아니라, 노드 별 상이한 weight를 가지고 가중합 하는 방식입니다. 즉, '나'한테 영향을 주는 '정도'까지 학습합니다.
가중치 업데이트 과정
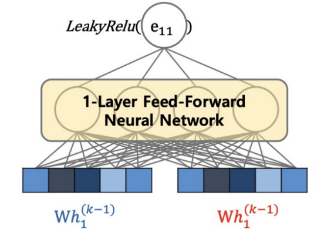
가중치 업데이트 계산
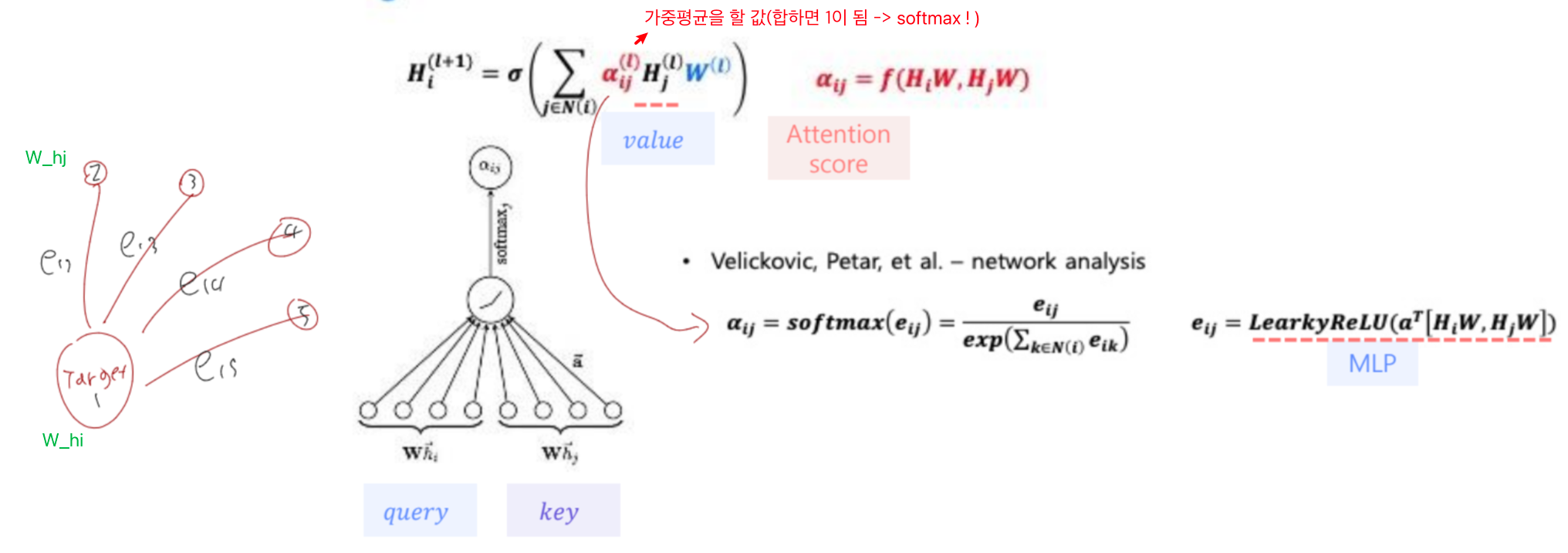
- '나'한테 영향을 주는 '정도'를 학습하기 위해 GAT에서는 Attention을 사용합니다.
- 를 통해 가중평균할 값. 즉, '정도'를 표현할 수 있습니다.
- 는 정도()에 softmax를 씌운 값입니다.
- : i와 j의 중요도
- Attention을 하는 방법들은 여러 가지가 있습니다.
- ex) 의 Attention을 구하고자 할 때,
- 1) 내적:
- 2) 내적(with learnable parameter):
- 3) concat & MLP:
- GAT에서는 concat를 사용하여 Attention을 계산합니다.
Multi-head attention(MHA)
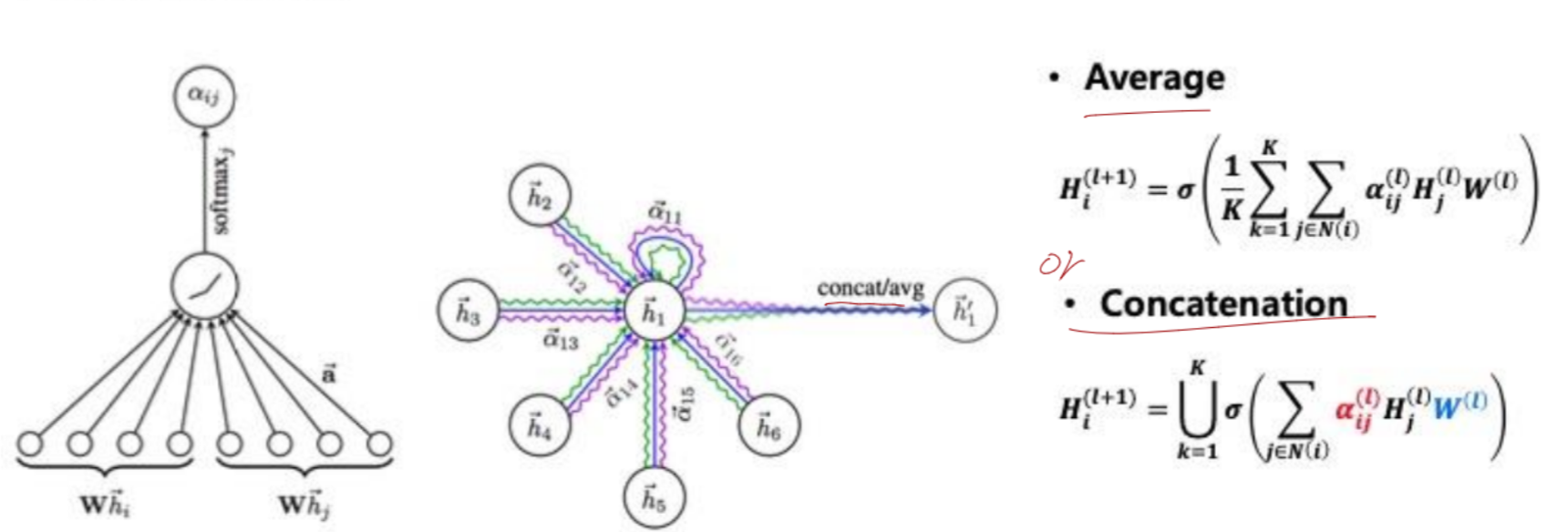
- GAT에서도 Multi-head attention을 사용할 수 있습니다.
- GAT에서의 MHA는 단순히 가중치 업데이터 계산 과정을 여러 번 수행한 것으로, 이를 Average하거나 Concatenation하여 사용합니다.
2-5. Receptive Field
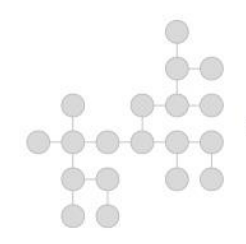
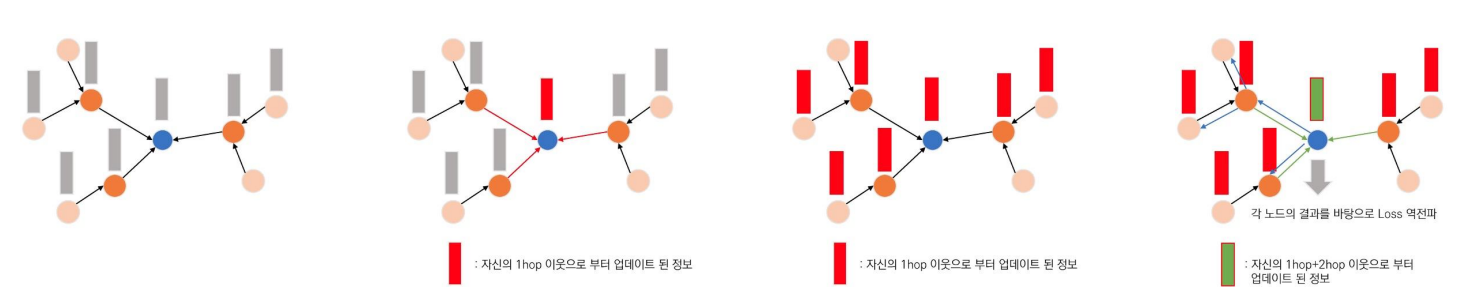
- 위와 같은 네트워크가 있습니다.
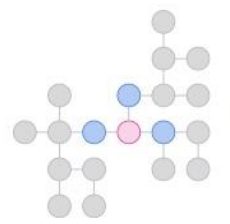
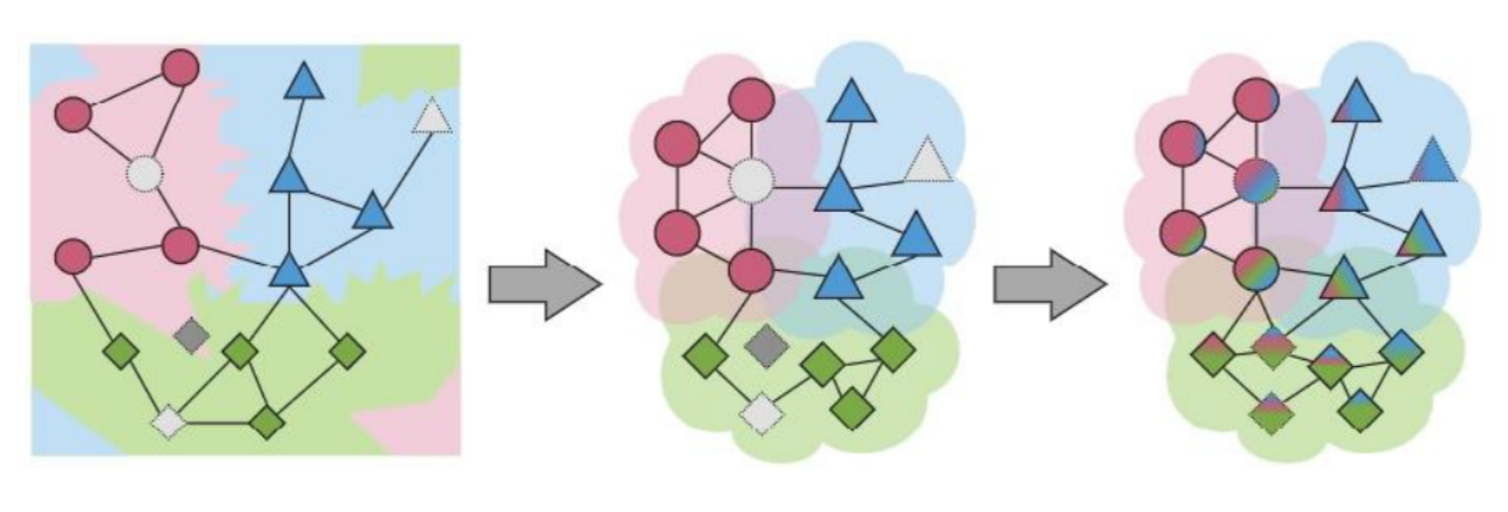
- 분홍색 원을 Target Node라고 했을 때, 한 번 GCN을 수행하면 자기 주변(한 칸) 이웃들의 정보를 모으게 됩니다.
- 한 번의 GCN을 거치면, 이와 같은 과정이 모든 노드들에 수행 될 것입니다.
- 즉, 한 번의 GCN이 수행된 후 Target Node의 바로 주변 이웃들은 그 옆 이웃들의 정보(Target Node로부터 두 번 떨어진 노드들의 정보)도 포함하고 있게 됩니다.
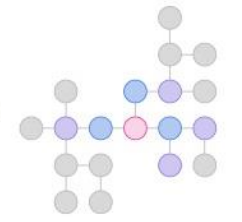
- 따라서 GCN을 N번 수행하게 되면, N번 떨어진 노드들의 정보까지 Target Node가 학습할 수 있게 되는 것입니다.
- CNN에서 Convolution을 여러 번 수행하면 Receptive Field가 넓어지는 것과 마찬가지로, GCN에서 Layer를 깊게 쌓으면 더 넓은 주변 정보를 가져올 수 있습니다.
- GNN에서는 이를 hop이라고 표현합니다.
k-hop: 주변 k의 정보를 관찰하는 것 -> 1-hop을 k번 반복하는 것과 같음
<주의> Over-Smoothing Issue
- GNN은 결국 주변 정보를 이용하여 Node들을 임베딩하는 것입니다. Layer가 너무 깊어지게 된다면 '주변 정보'가 아니게 될 수 있습니다.
- GCN에서 Layer 개수별 정확도
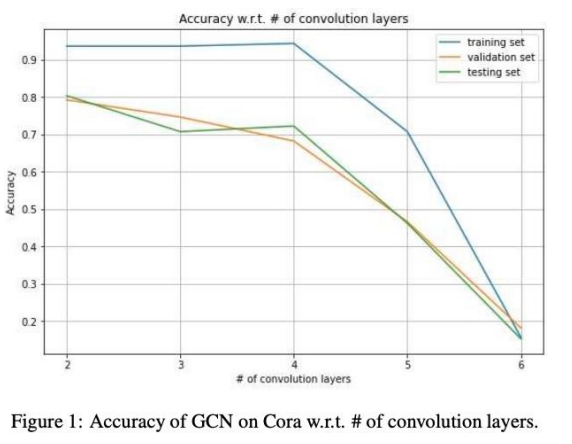
- GCN에서 Layer 개수별 정확도
- 이러한 Over-Smmothing Issue를 방지하기 위해 여러가지 방법을 적용할 수 있습니다.
- Node Dropout
- Edge Dropout
- Layer-wise Edge Dropout(Random Walk): Layer별로 Edge Dropout을 다 다르게 하는 것
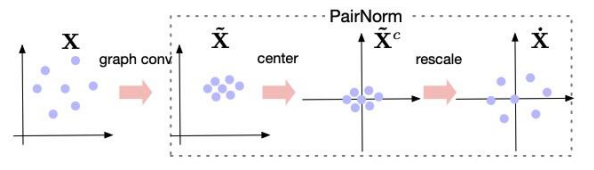
- PairNorm: centering + rescaling을 통해 펼치는 것
2-6. Aggregate(Message passing) & Combine(Update)
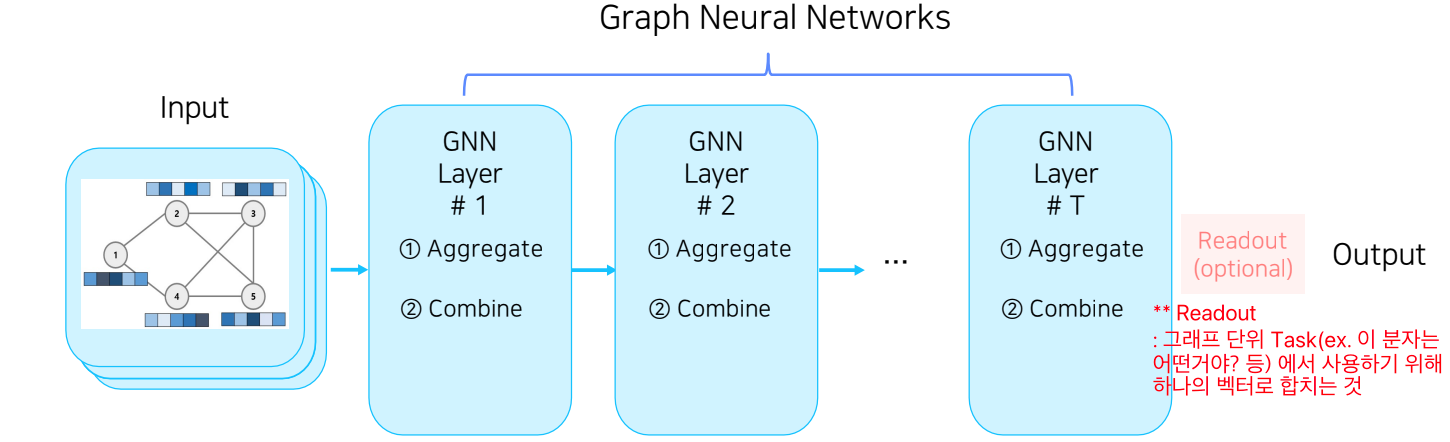
Aggregate(Message passing)
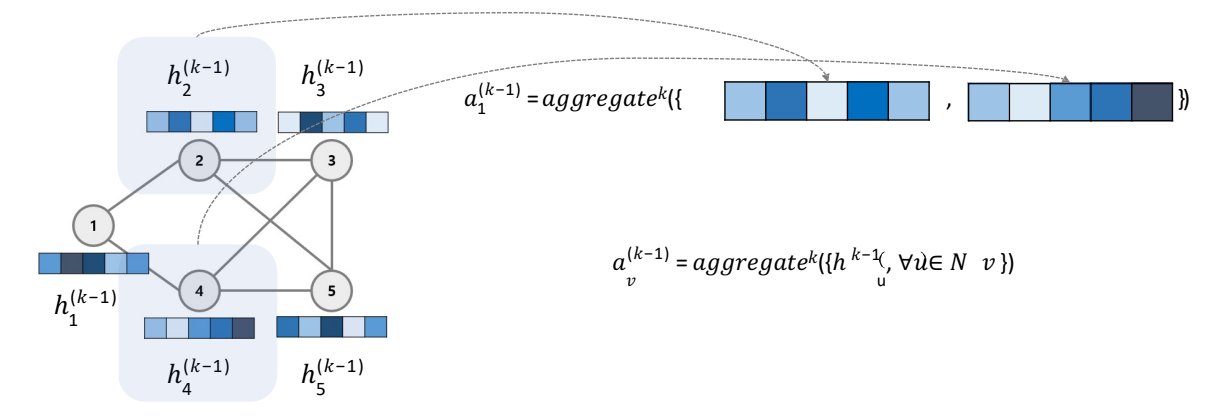
: 타겟 노드의 이웃 노드들의 k-1 시점의 hidden state를 결합하는 것입니다.
: 즉, 주변 노드들의 정보를 가져오는 단계입니다.
Combine(Update)
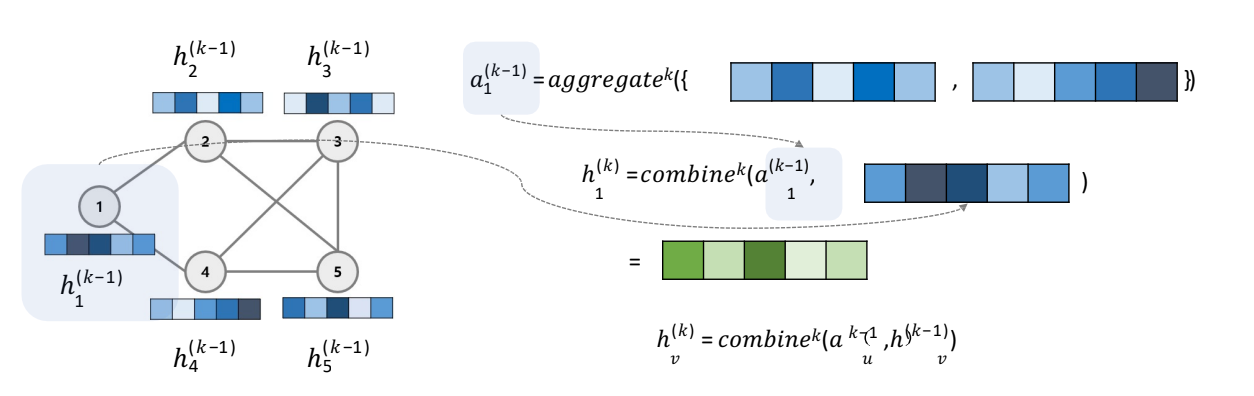
: k-1 시점 타겟 노드의 hidden state와 Aggregated information을 사용하여 k시점의 타겟 노드의 hidden state를 업데이트합니다.
: 즉, Aggregate에서는 자기 자신의 정보를 고려하지 않았으므로, 이를 고려해주는 것(combine)을 의미합니다.
->
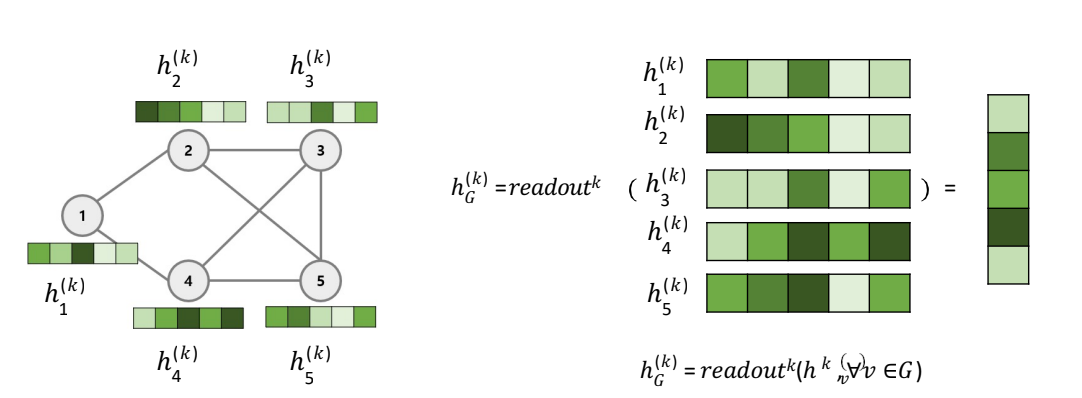
- Readout: K시점의 모든 Node들의 Hidden state를 결합하여 graph-level의 hidden state 생성하는 것입니다.
Message Passing 정리
- Message: 엣지 별 전파시킬 값 계산
(Target에게 얼만큼 줄 것인가?) - Aggregate(add, mean, ...): 노드 별 합산
(가져온 것을 어떻게 합칠 것인가?) - Update(=combine: concat, sum, ...): 합산 결과 반영
(원래 자기 것과 Aggregate된 것(주변정보)를 어떻게 합칠 것인가?)
Message Passing: GCN
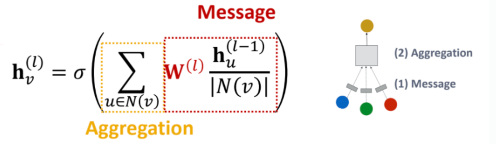
- 각 이웃 노드별로 얼만큼 message passing을 할 것인지(얼만큼 정보를 전달할 것인가?)가 핵심 포인트라고 할 수 있습니다.
- GCN에서는 이것이 단순 가중합(같은 비율만큼 합쳐짐)이었다면, GAT에서는 이를 Attention Score(Attention Coefficient)만큼 다르게 합칩니다.