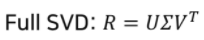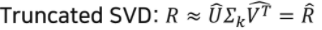
Model Based Collaborative Filtering(MBCF)
NBCF의 한계
- Sparsity & Scalability Issue
- Sparsity(희소성) 문제
- 데이터가 충분하지 않다면 추천 성능이 떨어짐(유사도 계산이 부정확함)
- 데이터가 부족하거나 혹은 아예 없는 유저, 아이템의 경우 추천이 불가능함(Cold Start)
- Scalability(확장성) 문제
- 유저와 아이템이 늘어날수록 유사도 계산이 늘어남
- 유저, 아이템이 많아야 정확한 예측을 하지만, 시간은 너무 오래걸리는 현상이 발생
- Sparsity(희소성) 문제
MBCF
MBCF란
- 항목 간 유사성을 단순 비교하는 것에서 벗어나 데이터에 내재된 패턴을 이용해 추천하는 CF 기법
- Parametric Machine Learning을 사용
- 주어진 데이터를 사용하여 모델을 학습
- 데이터 정보가 파라미터의 형태로 모델에 압축
- 모델의 파라미터는 데이터의 패턴을 나타내고, 최적화를 통해 업데이트
MBCF 특징
- 데이터에 숨겨진 유저-아이템 관계의 잠재적 특성/패턴을 찾음
- vs. NBCF
- 이웃기반 CF는 유저/아이템 벡터를 데이터를 통해 계산된 형태로 저장(aka. Memory-based CF)
- Model-based CF는 유저, 아이템 벡터는 모두 학습을 통해 변하는 파라미터
- vs. NBCF
- 현업에서 Matrix Factorization 기법이 가장 많이 사용됨
- 간단하면서도 좋은 성능을 보여줌
- 최근에는 MF 원리를 Deep Learning 모델에 응용하는 기법이 높은 성능을 냄
MBCF 장점(vs. NBCF)
1. 모델 학습/서빙
- 유저-아이템 데이터는 학습에만 사용되고 학습된 모델은 압축된 형태(파라미터)로 저장됨
- 이미 학습된 모델을 통해 추천하기 때문에 서빙 속도가 빠름
2. Sparsity/Scalability 문제 개선
- 이웃 기반 CF에 비해 sparse한 데이터에 대해서도 좋은 성능을 보임
(NBCF와 달리 Sparsity Ratio가 99.5%가 넘을 경우에도 사용 가능) - 사용자, 아이템 개수가 많이 늘어나도 좋은 추천 성능을 보임
3. Overfitting 방지
- 이웃기반 CF와 비교했을 때 전체 데이터의 패턴을 학습하도록 모델이 작동함
(이웃 기반 CF의 경우 특정 주변 이웃에 의해 크게 영향을 받을 수 있음(Overfitting))
4. Limited Coverage 극복
- 이웃기반 CF의 경우 공통의 유저/아이템을 많이 공유해야만 유사도 값이 정확해짐
(NBCF에서 유사도 값이 정확하지 않은 경우 이웃의 효과를 보기 어려움)
또 다른 이슈: Implicit Feedback
Implicit Feedback vs Explicit Feedback
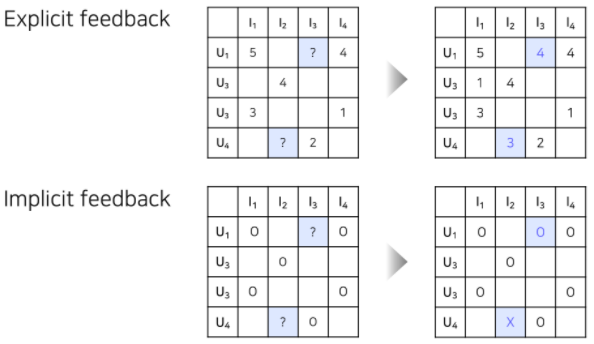
- Explicit feedback
- 영화 평점, 맛집 별점 등 item에 대한 user의 선호도를 직접적으로 알 수 있는 데이터
- Implicit feedback
- 클릭 여부, 시청 여부 등 item에 대한 user의 선호도를 간접적으로 알 수 있는 데이터
- 유저-아이템 간 상호작용이 잇었다면 1(positive)을 원소로 갖는 행렬로 표현 가능
- 그러나 상호작용하지 않았다고 해서 꼭 0을 원소로 두지도 않음)
-> 제공되는 데이터 중에서 Implicit feedback이 Explicit feedback에 비해 훨씬 많음(잘 이용할 수 있어야 함)
Latent Factor Model
Latent Factor Model이란
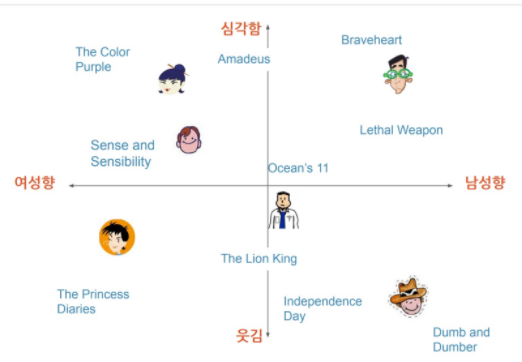
- 유저와 아이템 관계를 잠재적 요인으로 표현할 수 있다고 보는 모델
- 다양하고 복잡한 유저와 아이템의 특성을 몇 개의 벡터로 compact하게 표현
- 유저-아이템 행렬을 저차원의 행렬로 분해하는 방식으로 작동
(각 차원의 의미는 모델 학습ㅇ르 통해 생성되며, 표면적으로는 각 차원이 무엇을 의미하는지는 알 수 없음) - 같은 벡터 공간에서 유저와 아이템 벡터가 놓일경우 유저와 아이템의 유사한 정도를 확인할 수 있음
- 유저와 아이템 벡터가 유사하게 놓여있다면, 유사하다고 가정
Singular Value Decomposition(SVD)
SVD 개념
- Rating Matrix 에 대해 유저와 아이템의 잠재 요인을 포함할 수 있는 행렬로 분해
- 유저 잠재 요인 행렬
- 잠재 요인 대각 행렬(잠재요인의 중요도를 나타냄)
- 아이템 잠재 요인 행렬
- (선형대수에서 차원 축소 기법 중 하나로 분류되어 있음)
SVD 원리
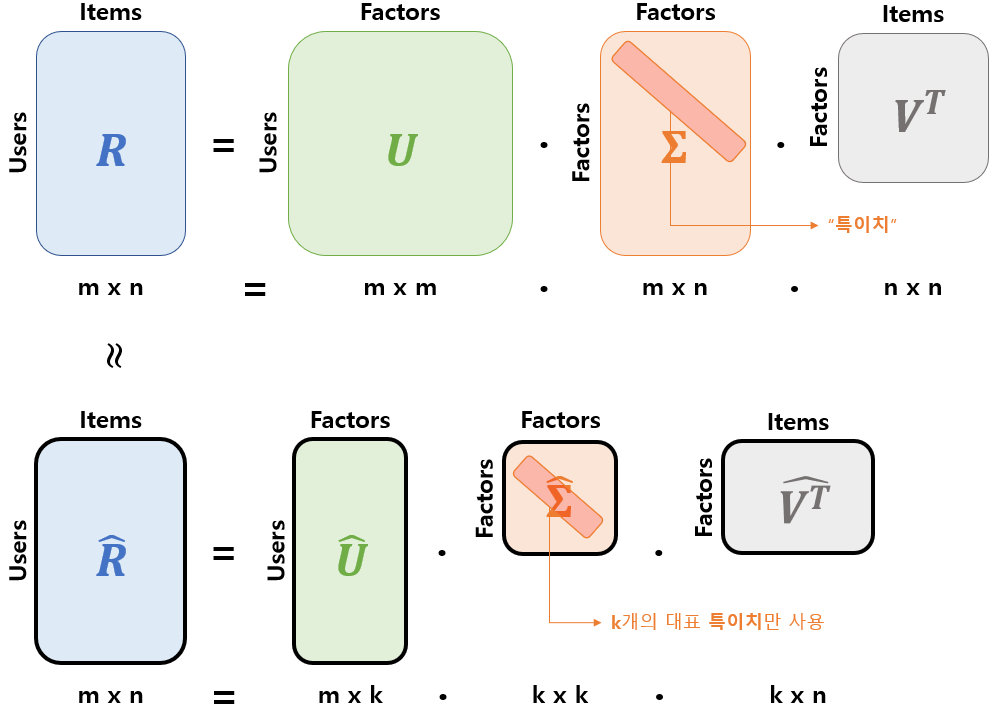
- : 유저와 Latent Factor의 관계
- 의 열벡터는 의 left singular vector
- : 아이템과 Latent Factor의 관계
- 의 열벡터는 의 right singular vector
- : Latent Factor의 중요도를 나타냄
- 을 고유값 분해해서 얻은 직사각 대각 행렬로 대각 원소들은 의 singular value(특이치)
- Full SVD 중 가장 값이 높은(대표 값) 몇 개(k개)나 골라서 압축시킨 형태
- 은 축소된 , , 에 의해 계산됨
- 몇 개의 특이치만을 가지고도 유용한 정보를 유지
- 분해된 행렬이 부분 복원되면서 가장 중요한 정보로 요약된다는 개념
SVD 한계점
- 분해(Decomposition)하려는 행렬의 Knowledge가 불완전할 때 정의되지 않음
- 그러나, 실제 데이터는 대부분 Sparse Matrix -> 불완전 !
- 따라서 Sparse Matrix분제를 해결하고자 결측된 entry를 모두 채우는 Imputation을 통해 Dense Matrix로 만들어 SVD를 수행하여야 함.
- 그러나, Imputation은 데이터의 양을 상당히 증가시키므로, Comutation 비용이 높아짐
SVD의 원리를 사용하되, 다른 접근 방법이 필요해짐 -> MF의 등장
Matrix Factorization(MF)
MF
Matrix Factorization이란
- User-Item 행렬을 저차원의 User와 Item의 Latent factor 행렬의 곱으로 분해하는 방법
(SVD의 개념과 유사) - 실제 관측된 선호도만 모델링에 활용(SVD와 차이점)하여 관측되지 않은 선호도를 예측하는 일반적인 모델을 만드는 것이 목표
- Rating Matrix를 P(유저 행렬)와 Q(아이템 행렬)로 분해하여 과 최대한 유사하게 을 추론(최적화)
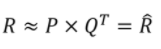
기본 MF 모델
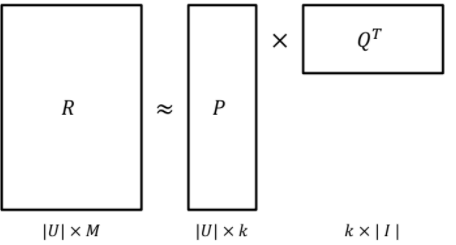
- 과 이 최대한 유사하도록 모델을 학습하는 과정
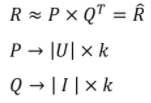
- 결국, 목적 함수를 정의하고, 이를 최적화하는 문제를 푸는 것.
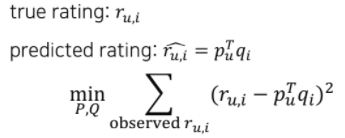
Objective Function
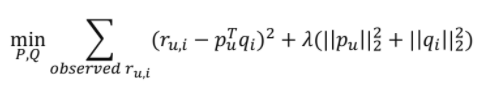
- : 학습 데이터에 있는 유저 u의 아이템 i에 대한 실제 rating
- : 유저(아이템) 의 Latent vector
- 최적화 문제를 통해 업데이트되는 파라미터임
- (상수)배 된 penalty term은 L2-정규화(regularization)을 의미
- 가 너무 커지지 않도록 하여 학습 데이터에 과적합되는 것을 방지
- Regularization Term에 곱해지는 의 크기에 따라 영향도가 달라짐
(너무 크면 weight가 제대로 변하지 않아서 underfitting이 일어남)(참고)
정규와의 대표적인 방법으로 L1, L2정규화가 있음

MF 학습(SGD)
확률적 경사하강법(Stochastic Gradient Descent, SGD)
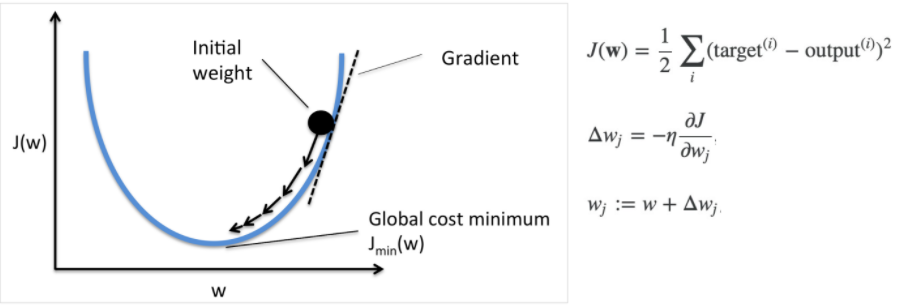
- = Loss
MF 모델에서의 SGD

MF +
- 기본적인 MF에 다양한 테크닉을 추가하여 성능을 향상시킴
- 논문
Adding Biases
어떤 유저는 모든 영화에 대해서 평점을 짜게 줄 수도 있음
(그 반대의 경우도 존재)
-> 따라서 전체 평균, 유저/아이템에 bias를 추가하여 예측 성능을 높임
- 기존 목적함수
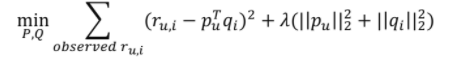
- Bias 추가된 목적함수
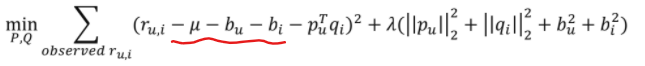
- Error
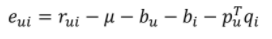
- Gradient의 반대 방향으로 를 업데이트
(참고: 는 learning rate.)
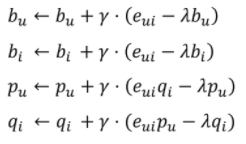
Adding Confidencd Level
모든 평점이 동일한 신뢰도를 갖지 않음
- ex)
- 대규모 광고 집행과 같이 특정 아이템이 많이 노출되어 클릭되는 경우
- 유저의 아이템에 대한 평점이 정확하지 않은 경우(Implicit Feedback)
-> 따라서 에 대한 신뢰도를 의미하는 추가
- 기존 목적 함수
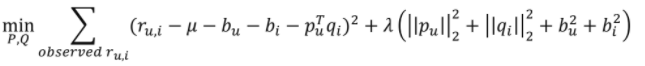
- Confidence level 추가된 목적 함수
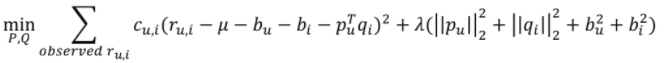
Adding Temporal Dynamics
시간에 따라 변하는 유저, 아이템의 특성을 반영하고 싶음
- ex)
- 아이템이 시간이 지남에 따라 인기도가 떨어짐
- 유저가 시간이 흐르면서 평점을 내리는 기준이 바뀜(엄격해지는 등)
-> 따라서 학습 파라미터가 시간을 반영하도록 모델을 설계(시간을 반영한 평점 예측)
- 시간을 반영한 평점 예측
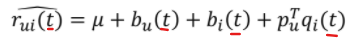
- ex)
MF for Implicit Feedback
Alternative Least Square(ALS)
- Implicit Feedback 데이터에 적합하도록 MF 기반 모델을 설계하여 성능을 향상시킴
- 논문
ALS란
- Basic Concept
- 유저와 아이템 매트릭스를 번갈아가면서 업데이트
(두 매트릭스 중 하나를 상수로 놓고 나머지 매트릭스를 업데이트) - 가운데 하나를 고정하고 다른 하나로 least-squar(최소제곱) 문제를 푸는 것
- 가운데 하나를 고정할 경우, 목적함수가 quadratic form(이차 형식)이 되어 convex해짐
- (즉, 경사하강법을 통해 찾는 최저점이 단 하나(Global minumum)만 존재)
- (Non-convex하면(p, q가 계속 바뀌게 되면), 여러 곳의 지역 최저점(local minimum)을 가질 수 있음)
- 유저와 아이템 매트릭스를 번갈아가면서 업데이트
- vs. SGD
- Sparse한 데이터에 대해 SGD보다 더 Robust함
- 대용량 데이터를 병렬처리하여 빠른 학습 가능
ALS 목적함수(for Explicit Feedback)
- 기존 MF 목적함수
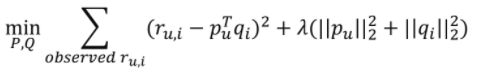
- ALS 목적함수: 아래 수식을 사용하여 를 번갈아가며 업데이트(For convex)
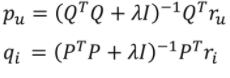
MF for Implicit Feedback
- 참고) SGD나 ALS로 동일하게 풀 수 있음
(논문에서는 ALS 연산을 통해 좀 더 효율적으로 연산하는 방법을 제안함.)
Implicit Feedback 고려
- 기존 Explicit Dataset을 다룰 땐, 0으로 남은 데이터들은 버리고 학습을 진행함.
- 즉, Explicit Feedback보다 훨씬 많은 양의 Implicit Feedback 데이터를 버리게 됨.
- ALS에서는 값을 통해 0으로 남아있는 데이터들에 대한 예측 값도 Latent Factor 학습에 포함시킴.
Preference
- 유저 u가 아이템 i를 선호하는지 여부를 binary로 표현
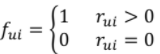
Confidence
- 유저 u가 아이템 i를 선호하는 정도를 나타내는 increasing function
- 는 positive feedback과 negative feedback 간의 상대적인 중요도를 조정하는 하이퍼파라미터임.
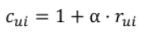
Implicit Feedback을 고려한 MF(SGD) 목적함수
- 기존 목적함수(Explicit Feedback)
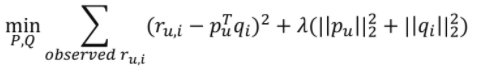
- 새로운 목적함수(Implicit Feedback)
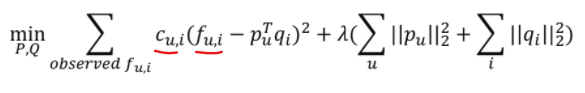
Implicit Feedback을 고려한 MF(ALS) 목적함수
- 기본 해의 형태(Explicit Feedback)
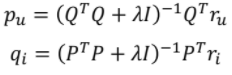
- 새로운 해의 형태(Implicit Feedback)
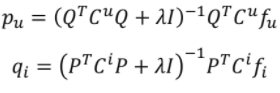
Bayesian Personalizaed Ranking(BPR)
- Implicit Feedback 데이터를 활용해 MF를 학습할 수 있는 새로운 관점을 제시한 논문
Personalized Ranking
핵심 아이디어
- point-wise approaches vs pair-wise approaches
- point-wise
- Loss function에서 한번에 하나의 아이템만 고려함.
- input:
Score(User, Item) - item과 item의 순서 관계 등을 무시한다는 단점이 존재
- pair-wise
- Loss function에서 한번에 2개의 아이템을 고려함.
- input:
Score(User, Pos, Neg) - input에 pos item과 neg item이 동시에 들어가면서, 자연스레 이들 간 Rank를 고려할 수 있게 됨.
- 일반적으로 pos item보다 neg item이 훨씬 많기 때문에 sampling 기법 등을 사용함.
- (further) list-wise approaches
- Loss function에서 한번에 전체의 아이템을 고려함.
- point-wise
- 기존 추천 방식
- 관측되지 않은 데이터는 모두 negative feedback으로 간주했음.
- 이때, 비관측된 데이터은 '실제 negative feedback' + 'missing value(유저가 놓친 아이템. 즉, 미래에 구매할 가능성이 있는 아이팀)' 이었음.
- Personalized Ranking을 반영한 최적화
- 유저가 item i보다 j를 좋아한다면 이 정보를 사용해 MF의 파라미터를 학습함
- 유저 u에 대해 item i > item j 라면, 이는 유저 u의 personalized ranking.
-> 즉, 유저의 아이템에 대한 선호도 랭킹을 생성하여 이를 MF의 학습 데이터로 사용 (아이템에 대한 순위를 구하는 것에 초점을 맞춤).
접근
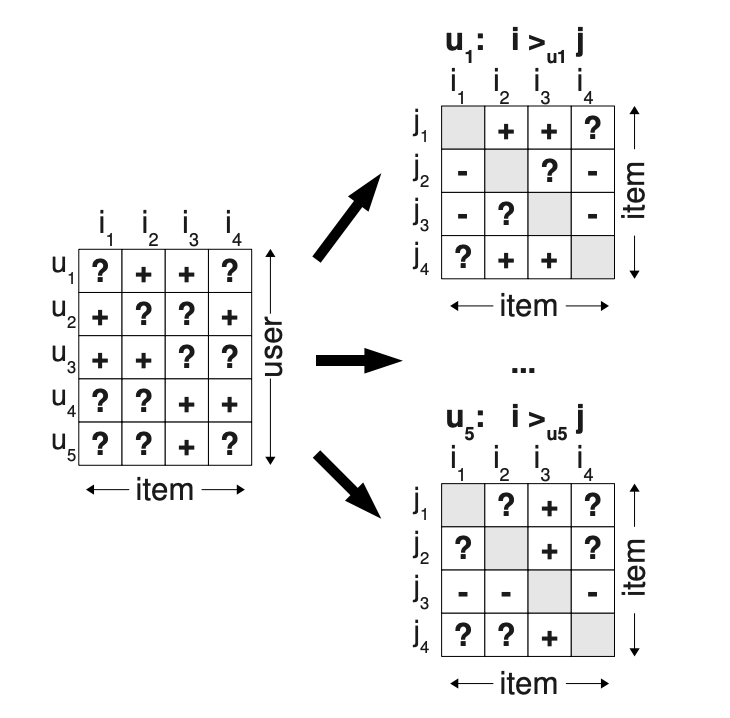
- 가정
- 관측된 item을 관측되지 않은 item보다 선호
- 관측된 아이템끼리는 선호도를 추론할 수 없음
- 관측되지 않은 아이템끼리도 선호도를 추론할 수 없음
- 특징
- 관측되지 않은 item들에 대ㅐㅎ서도 정보를 부여하여 학습
- 관측되지 않은 item들에 대해서도 ranking이 가능
(관측된 item을 관측되지 않은 item보다 선호)
- 학습 데이터 생성
- 유저 가 선호하는(관측된) 아이템들을 라고 하면,

- 유저 가 선호하는(관측된) 아이템들을 라고 하면,
- 위 그림에서, 유저 의 선호도 데이터 예시
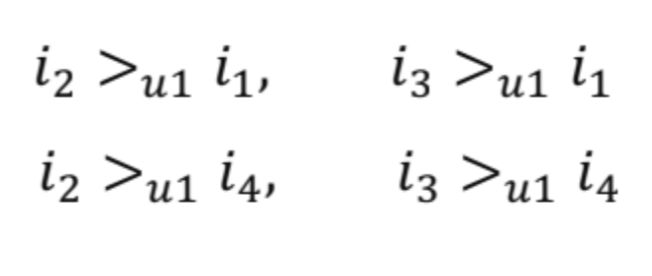
최대 사후 확률 추정(Maximum A Posterior)
: 사후확률이 최대가 되는 파라미터를 학습
- Bayes 정리에 의해,
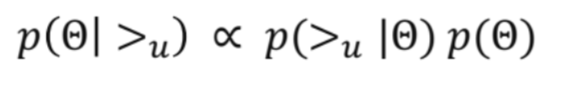
- 사전 확률(prior): , 파라미터에 대한 사전 정보
- 가능도(likelihood): , 주어진 파라미터에 대한 유저의 선호 정보의 확률
- 사후 확률(posterior): , 주어진 유저의 선호 정보에 대한 파라미터의 확률
: Posterior를 최대화 한다는 것 -> 주어진 유저 선호 정보를 최대한 잘 나타내는 파라미터를 추정하는 것
Likelihood:
:모든 유저 선호 정보(에 대한 likehood
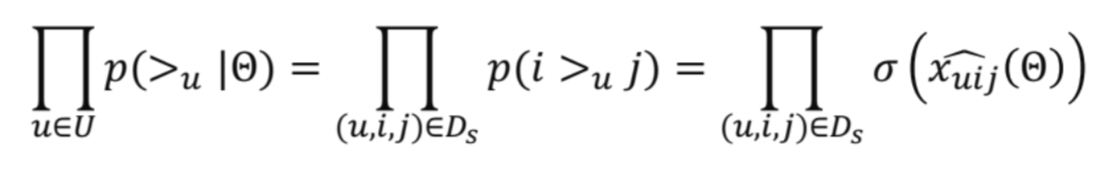
- 유저 의 벡터가 , 아이템 의 벡터가 일 때, 유저 가 아이템 를 보다 좋아할 확률은
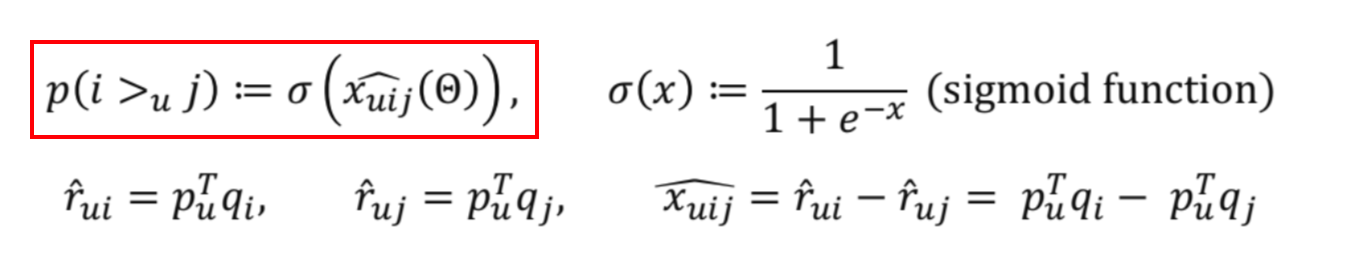
Prior:
: 파라미터에 대한 사전 확률은 정규분포를 따른다고 가정
- 평균이 모두 0이고, 공분산 행렬이 인 정규분포
- 공분산 행렬 는 (단위행렬)로 설정하여 하이퍼파라미터의 계수를 조정
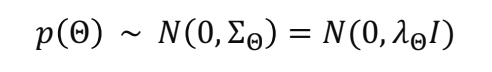
BPR 목적함수

- 위에 나온 loss 식을 최대화 하는 방향으로 모델을 학습
- BPR-OPT 식에서, = - (difference between i and j)
- 이때 각 와 는 latent factor model의 결과값으로 정의될 수 있음
- = - = -
(i: positive item, j: negative item)
- = - = -
- MF와 달리 BPR은
- pair-wise optimization
- classification objective
LEARNBPR
- Objective인 BPR-OPT는 미분가능하기 때문에 Gradient Descent로 Optimization을 수행함. 그러나 논문에서는 일반적인 Gradient Descent가 적절한 학습 방법이 아니라고 말하고 있음.
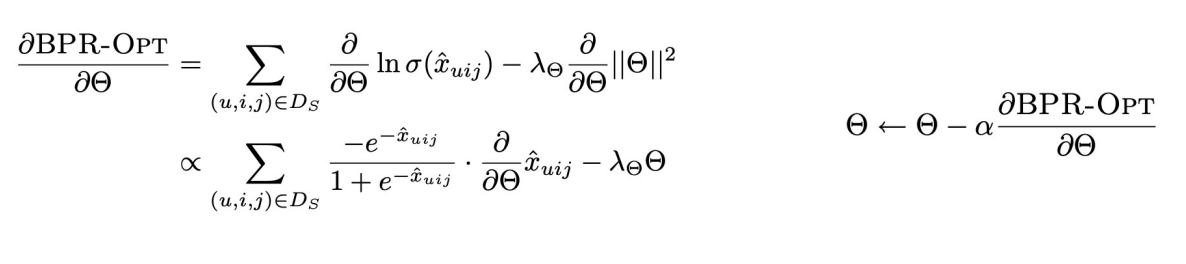
LEARNBPR

- 논문에서는 Bootstrap 기반의 SGD를 사용
{ \ }
( : 유저의 선호 정보를 사용한 학습 데이터) - 일반적인 SGD를 사용하면,
- 보통 i보다 j가 훨씬 많기 때문에 학습의 비대칭 발생
- 그러나, triples 단위로 랜덤 샘플링하면, i와 j의 비대칭 학습을 해소할 수 있음.
- 유저 의 벡터를 아이템 의 벡터를 라고 하면,
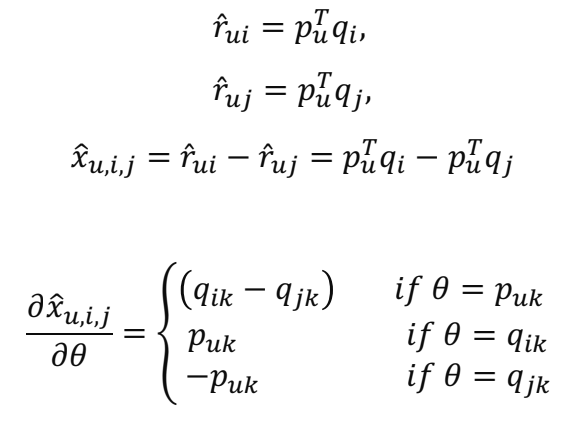
BPR 요약
- Implicit Feedback 데이터만을 활용해 아이템 간의 선호도 도출
- Maximum A Posterior 방법을 통해 파라미터를 최적화
- LEARNBPR이라는 Bootstrap 기반의 SGD를 활용해 파라미터를 업데이트(데이터의 비대칭 해결)