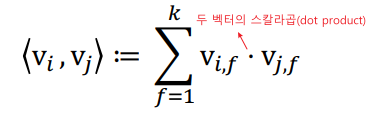[boostcamp-ai-tech][RecSys] Context-aware Recommendation: FM, FFM, GBM, (Fuse Context with Latent Cross)
RecSys
What is Context-aware Recommendation
개요
-
앞서 배운 MF 등의 모델들은 개별 유저와 아이템 간 상호작용을 2차원 행렬로 표현
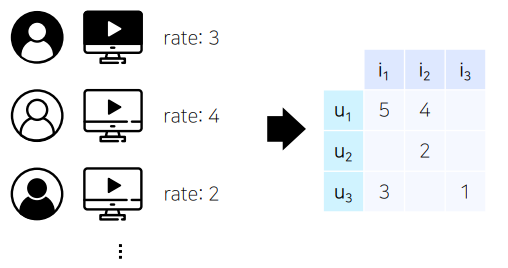
- 유저의 데모그래픽이나 아이템의 카테고리 및 태그 등 여러 특성(feature)들을 추천시스템에 반영할 수 없었음.
- 상호작용 정보가 부족할 경우, 'cold start'에 대한 대처가 어려움
-
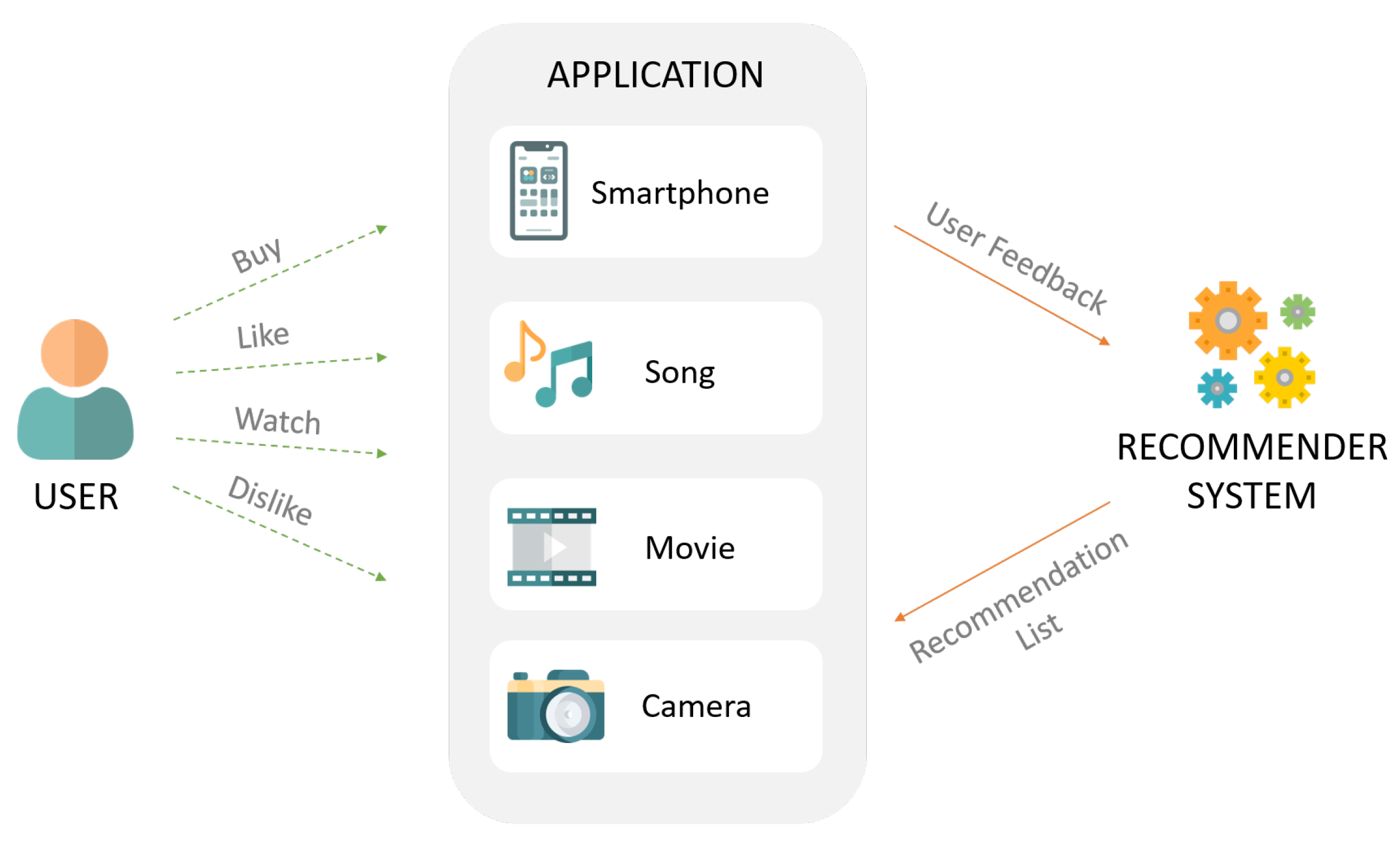
컨텍스트 기반 추천시스템
: 유저와 아이템 간 상호작용 정보 뿐 아니라, 맥락(context)적 정보도 함꼐 반영하는 추천 시스템
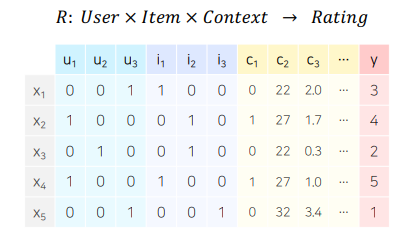
- X를 통해 Y의 값을 추론하는 일반적인 예측 문제에 두로 적용 가능
활용 예시: CTR Prediction
Click-Through Rate Prediction (CTR Prediction)
- CTR 예측: 유저가 주어진 아이템을 클릭할 확률을 예측하는 문제
- 예측해야 하는 y값은 클릭 여부, 즉 binary classification 문제에 해당.
- 모델에서 출력한 실수 값을 시그모이드(sigmoid)에 통과시키면 (0, 1) 사이의 예측 CTR 값이 됨.
- 광고 등에서 주로 사용됨
- 광고가 노출된 상황의 다양한 유저, 광고, 컨텍스트 피쳐를 모델의 입력 변수로 사용
- 예측해야 할 y값은 binary classification 문제임.
- 따라서 기본적으로 Logistic Regression으로 접근할 수 있으나, 변수간 상호작용을 고려하진 않음
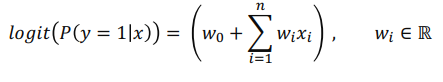
- 변수 간 상호작용을 고려하는 Polynomial Model을 사용할 수 있음. 하지만 파라미터 수가 급격히 증가한다는 한계가 있음
-> 대안: FM, FFM (뒤쪽에서 다룰 예정)
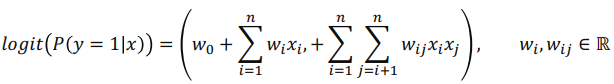
- 따라서 기본적으로 Logistic Regression으로 접근할 수 있으나, 변수간 상호작용을 고려하진 않음
사용 데이터
- CTR 예측 문제에 사용되는 데이터를 구성하는 요소는 대부분 Sparse feature임
- Sparse Feature: 벡터로 표현했을 때 비교적 넓은 공간에 분포하는 범주형 변수(Categorical Data)
- ex) 유저/아이템 ID, 요일, 분류, 키워드, 태그 등
- ex)
월요일 -> [1, 0, 0, 0, 0, 0, 0]
수요일 -> [0, 0, 1, 0, 0, 0, 0]
- 그러나, One-hot Endoing에는 한계가 존재
- 파라미터 수가 너무 많아질 수 있음
- 학습 데이터에 등장하는 빈도에 따라 특정 카테고리가 overfitting/underfitting 될 수 있음
- 따라서 피쳐 임베딩을 한 이후에 이 피쳐를 가지고 예측을 하기도 함
- 자연어 처리에 사용되는 텍스트 임베딩 기법들이 흔히 적용됨
(Item2Vec, LDA, BERT, ...)
- 자연어 처리에 사용되는 텍스트 임베딩 기법들이 흔히 적용됨
Factorization Machine (FM)
- SVM과 Factorization Model(FM 등)의 장점을 결합한 FM을 처음 소개한 논문
- 논문
개요
-
Factorization Machine(FM) 등장 배경
- 딥러닝이 등장하기 이전에는 서포트 벡터 머신(SVM)이 가장 많이 사용되는 모델이었음
- 커널 공간을 활용하여 비선형 데이터셋에 대해 높은 성능을 보임
- CF 환경에서는 SVM보다 MF 계열의 모델이 더 좋은 성능을 보였음.
- 매우 희소(Sparse)한 데이터에 대해서는 SVM이 좋은 성능을 내지 못함
- 그러나 MF 모델은 특별한 환경 혹은 데이터에서만 적용할 수 있음.
- X: (유저, 아이템) -> Y: Rating
- MF는 위와 같은 형태로 이루어진 데이터에 대해서만 적용이 가능함
--> 두 모델의 장점을 결합
- 딥러닝이 등장하기 이전에는 서포트 벡터 머신(SVM)이 가장 많이 사용되는 모델이었음
FM 공식

- Factorization Term은 polinomial model과 비슷하지만, 의 상호작용을 라는 파라미터 하나로만 표현했던 것과 달리 두 개의 k차원(factorization dimension)의 학습 파라미터로 표현
- Factorization Term에서 학습 파라미터
참고) FM의 공식을 풀어 시간복잡도를 줄일 수도 있음

FM의 활용
Sparse한 데이터셋에서의 예측
-
평점 데이터 = {(유저1, 영화2, 5점), (유저3, 영화1, 4점), ...}
- 일반적인 CF 문제의 입력 데이터와 같음
-
위의 평점 데이터를 일반적인 입력 데이터로 바꾸면, 입력 값의 차원이 전체 유저와 아이템 수만큼 증가함.
- 예시)

- 예시)
-
FM을 활용한 평점 예측 예시)
: 유저 A의 영화 ST에 대한 평점을 어떻게 예측할까?
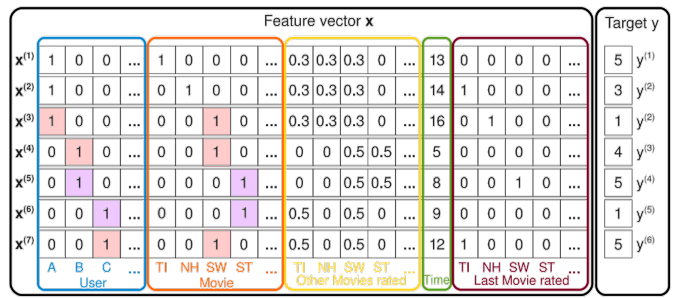
-
: 유저 B, C의 영화 ST에 대한 평점 데이터를 통해 학습됨.
- 유저 B, C는 ST외에 다른 영화도 평가했음.
-> 예를 들어, 다른 영화를 SW라고 한다면, ST가 SW에 비해 어떤 특성이 있는지 학습될 것임.
- 유저 B, C는 ST외에 다른 영화도 평가했음.
-
: 유저 B, C가 유저 A와 공유하는 영화 SW의 평점 데이터를 통해 학습됨.
- 유저 A가 B, C에 비해 어떤 특성이 있는지 학습될 것임.
-> 이와 같이 둘의 직접적인 상호작용 데이터는 없지만, 다른 데이터를 통해 각각의 Factorization 파라미터가 학습될 것이고, 그 파라미터를 통해 예측을 할 수 있음(가 FM모델을 통해 학습되기 때문에 상호작용이 반영됨).
- 예시에 존재하는 다양한 context들도 이와 같이 상호작용이 반영됨.
-
FM의 장점
- SVM에 비해
- 매우 Sparse한 데이터에 대해 높은 예측 성능을 보임
- 선형 복잡도 를 갖기 때문에 큰 학습 데이터에 대해서요 빠르게 학습이 가능
- 모델 학습에 필요한 파라미터의 개수도 선형적으로 비례함
- Matrix Factorization에 비해
- 여러 예측 문제(회귀, 분류, 랭킹 등)에 모두 활용 가능한 범용적인 지도학습 모델
- 유저, 아이템 ID 외에 다양한 부가 정보들을 모델의 피쳐로 사용할 수 있음
Field-aware Factorization Machine (FFM)
- FM의 변형된 모델인 FFM을 제안하여 더 높은 성능을 보인 논문
- 논문
개요
FFM의 등장 배경
-
FM은 예측 문제에 두루 적용 가능한 모델로, 특히 Sparse 데이터로 구성된 CTR 예측에서 좋은 성능을 보임
-
FFM은 FM을 발전시킨 모델로서 PITF 모델에서 아이디어를 얻음
- PITF: 3차원으로 MF를 확장시킨 모델
- PITF에서는 (user, item, tag) 3개의 필드에 대한 클릭률을 예측하기 위해
(user, item), (item, tag), (user, tag) 각각에 대해서 서로 다른 Latent Factor를 정의하여 구함.
-> 이를 일반화하여 여러 개의 필드에 대해서 Latent Factor를 정의한 것이 FFM
(사용자가 정의하는 개수만큼 늘려서 Latent Factor를 정의)FFM의 특징
-
입력 변수를 필드(field)로 나누어, 필드별로 서로 다른 Latent Factor를 가지도록 Factorize 함.
-
field는 모델을 설계할 때 함꼐 정의되며, 같은 의미를 갖는 변수들의 집합으로 설정함
- 유저: 성별, 디바이스, 운영체제, ..
- 아이템: 광고, 카테고리, ...
- 컨텍스트: 어플리케이션, 배너, ..
-> CTR 예측에 사용되는 피쳐는 이보다 훨씬 다양한데, 피쳐의 개수만큼 필드를 정의하여 사용할 수 있음.
FFM 공식

FM과의 비교
- 예시) 광고 클릭 데이터가 존재하고, 사용할 수 있는 Feature가 총 세 개(Publisher, Advertiser, Gender)일 때,
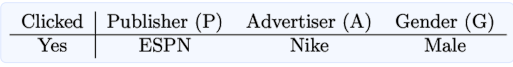
| FM | FFM |
|---|---|
| - 필드가 존재하지 않음 | - 각각의 feature를 필드 P, A, G로 정의 |
| - 하나의 변수에 대해 Factorization 차원 ()만큼의 파라미터를 학습 | - 하나의 변수에 대해 필드 개수()와 Factorization 차원()의 곱(=)만큼의 파라미터를 학습 |
| (: Linear Term, factorization term | (: Linear Term, factorization term) |
- Linear vs FM vs FFM
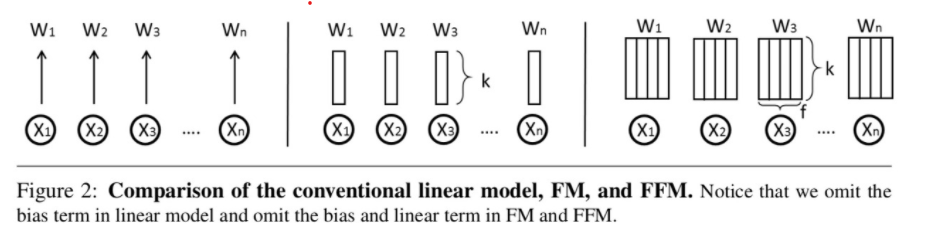
FFM 필드 구성
Categorical Feature

Numerical Feature

-
ex) discretize: field{age}
<=20 20~30 30~40 >40 0 1 0 0 1 0 0 0 0 0 0 1
Gradient Boosting Machine (GBM)
- Gradient Boosting Machine을 통한 CTR 예측
개요
GBM: CTR 예측을 통해 개인화된(personalized) 추천시스템을 만들 수 있는 또 다른 대표적인 모델
- 8개의 오픈 CTR 데이터셋에 대해 다른 추천 모델(FM계열 포함)보다 높은 성능을 보임
Boosting이란
- 앙상블(ensemble) 기법의 일종
- 앙상블: 모델의 편향에 따른 예측 오차를 줄이기 위해 여러 모델을 결합하여 사용하는 기법
- 의사결정 나무로 된 week learner들을 연속적으로 학습하여 결합하는 방식
- weak learner: 정확도와 복잡도가 비교적 낮은 간단한 분류기
- 연속적: 이전 단계의 weak learner가 취약했던 부분을 위주로 데이터를 샘플링하거나 가중치를 부여해 다음 단계의 learner를 학습한다는 뜻
- Boosting 기반 모델
GBM
- Gradient descent를 사용하여 loss function이 줄어드는 방향(negative gradient)으로 weak learner들을 반복적으로 결합함으로써 성능을 향상시키는 Boosting 알고리즘

Gradient Boosting as Residual Fitting
: 통계학적 관점에서, Gradient Boosting은 잔차(residual, 실제 값과 예측 값의 차이)를 적합(fitting)하는 것으로 이해할 수 있음.
- 이전 단계의 weak learner까지의 residual을 계산하여, 이를 예측하는 다음 weak learner를 학습함
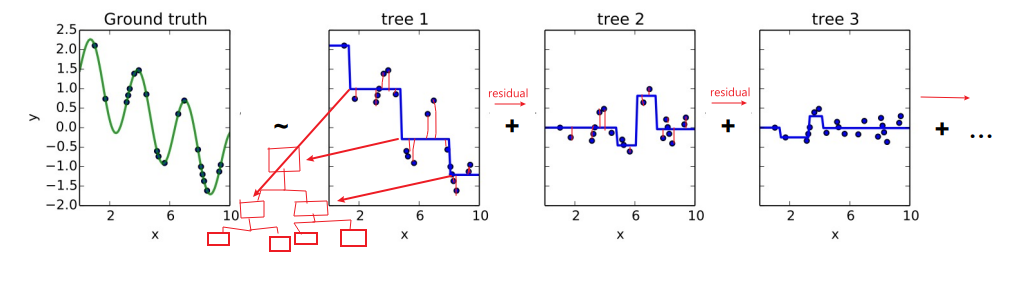
- 회귀 문제에서는 예측값으로 residual을 그대로 사용
- 분류 문제에서는 log(odds)값을 사용
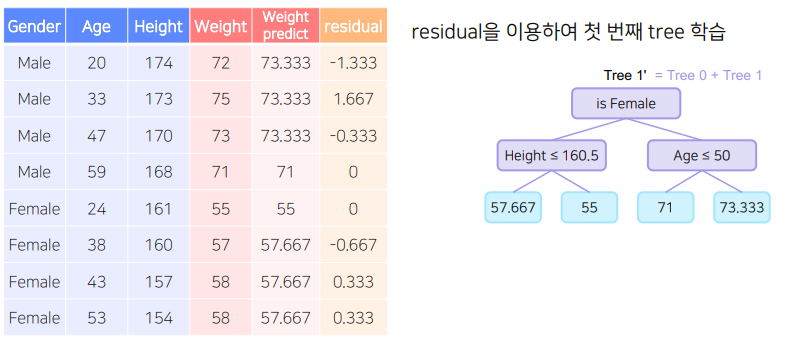
학습 방법(순서)
- A 모델은 전체 데이터의 target의 평균으로 예측 값을 만든고, 잔차(실제값 - 예측값)을 구한다.
이때, 이 잔차는 B모델이 학습할 정답이 된다. - B 모델은 A모델의 잔차를 맞추는 방식으로 학습을 진행한다.
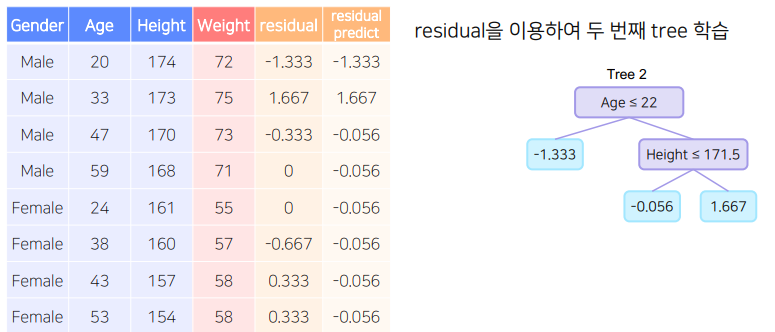
새로운 잔차 = 실제 값 - (A모델의 예측 값(평균 값) + lr * B모델의 예측 값) - (2)번을 반복한다.
새로운 잔차(C) = 실제 값 - (A모델의 예측 값 + lr B모델의 예측 값 + lr C모델의 예측 값) - 손실 함수 값이 일정 수준 이하로 떨어지거나, leaf node에 속하는 데이터의 수가 적어지면 멈춘다.
GBM 예시
-
A모델
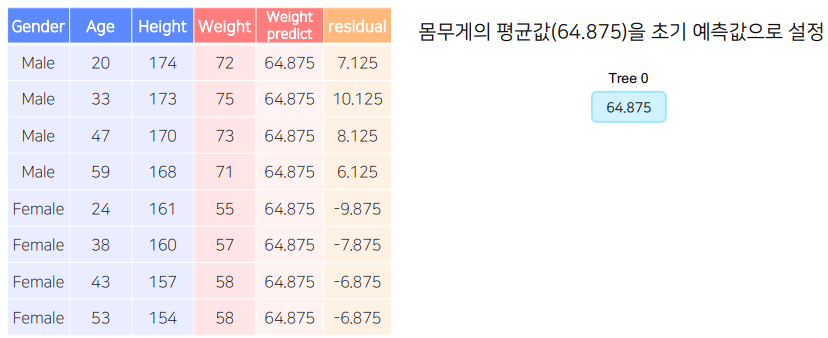
-
B모델
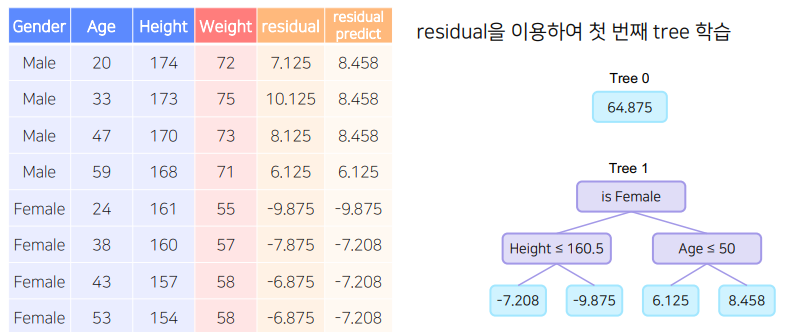
- C모델
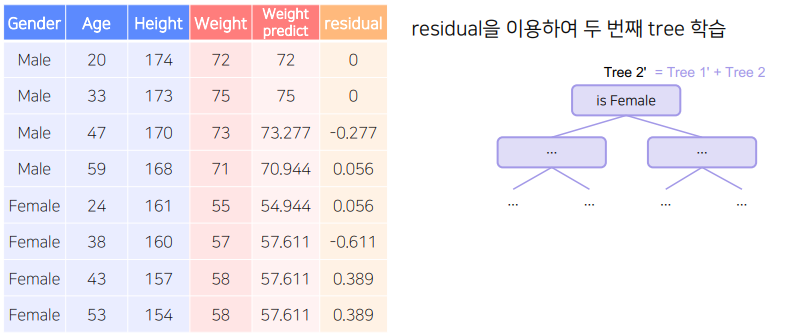
- 반복 -> 손실함수 값이 일정 수준 이하로 떨어지거나 leaf node에 속하는 데이터 수가 적어지면 멈춤
GBM 알고리즘의 장단점
- 장점
- 대체로 Random forest보다 나은 성능을 보임
- 단점
- 느린 학습 속도
- 과적합 문제
How to Fuse Context Effectively
- 2018년, Google YouTube Recommender 팀은 여러가지 context를 효과적으로 융합하기 위한 방법으로서 Latent Cross(element-wise product) 방법을 제안함.
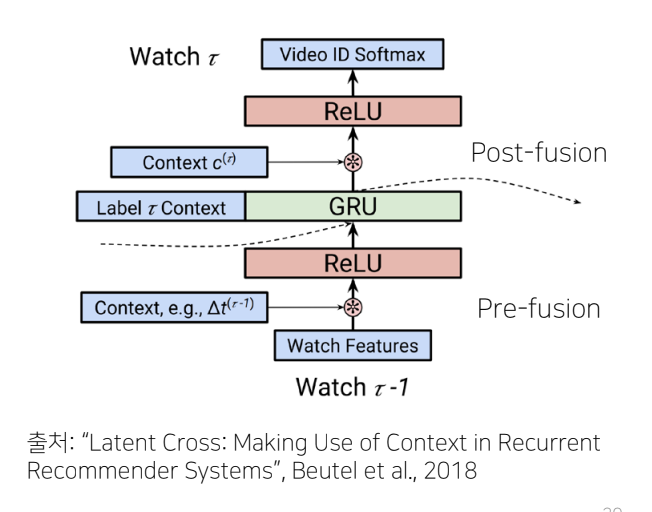
- Latent Cross Fusion between the hidden representation and the context vector
- Using multiple context vectors(e.g., time, device)
-Idea: 를 zero-mean Gaussian으로 초기화함으로써, hidden representation의 mask or attention mechanism으로 해석될 수 있음. 만약 context가 의미가 없다면 (
- Latent Cross Fusion between the hidden representation and the context vector
- 2021년, SIGIR2021 Workshop에서 우승한 솔루션
"transformers with multi-modal features and post-fusion context for e-commerce session-based recommendation", Moreira et al., 2021
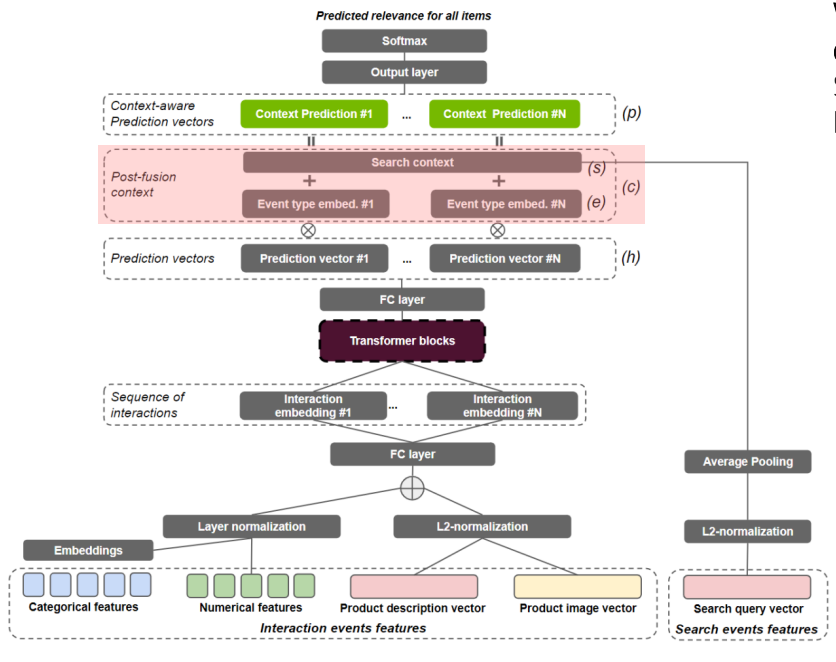
- (contextual vector) =
- : event type embedding
- : search context
- : embedding of a boolean feature that indicates whether the item to be predicted is a infrequent item or not
- (contextual vector) =