Handwritten Mathematical Expression Recognition with Bidirectionally Trained Transformer

Study·2023년 6월 23일

AI

목록 보기

14/15

논문 및 이미지 출처 : https://link.springer.com/chapter/10.1007/978-3-030-86331-9_37

Abstract

Encoder-decoder 로 Handwritten Mathematical expression Recognition (HMER) 에서 좋은 진척을 뵈지만, 여전히 image feature 에 attention 을 align 하는데 어려움이 존재한다.

보통 decoder 부분을 RNN 기반으로 만들어, 긴 LaTeX sequence 처리에 비효율적이다.

본 논문에선 transformer 기반의 decoder 를 채용하여 RRN 베이스를 교체한다.

또한 새로운 훈련 전략인 bidirectional language modeling 으로 transformer 의 잠재력을 이용한다.

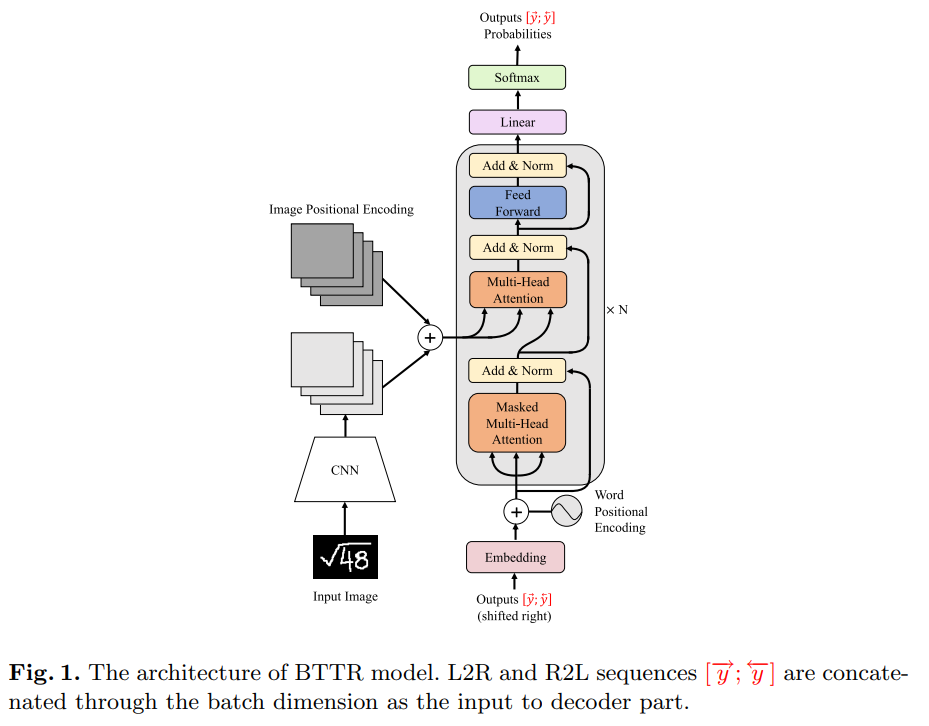
data augmentation 을 사용하지 않고 다른 방법과 비교하여 CROHME 2014, 2016, 2019 에서 성능 향상을 얻었다.

1 Introduction

encoder-decoder 는 최근 다양한 task 에서 좋은 성능을 낸다. HMER 또한 최근 encoder-deocoder 를 사용한다.

하지만, 다양한 각도에 대해 coverage 의 부족 문제가 존재하며, 두 가지 문제가 있다.

Over-parsing : 이미지 일부 영역이 여러번 중복되어 번역
Under-parsing : 일부 영역이 미번역

RNN 베이스는 또한 long-term dependency 문제로 gradient vanishing 를 야기한다.

전통적인 NLP 와 비교하여, LaTeX 마크업 언어로서 명확하고 뚜렷한 syntactic 구조를 가지고 있다. (예; "{", "}" 는 한 쌍으로 나타남)

RNN 베이스 만으로는 LaTeX sequence 를 다룰 때 "{" 와 "}" symbol 의 먼 거리 간의 관계를 모델링 하기는 어려우며, 이는 LaTeX syntax 의 awareness 부족으로 나타난다.

일반적으로 autoregressive 모델은 left-to-right (L2R) 방향으로 추론하며, 이는 unbalanced outputs 을 생성하는 문제가 있다.

이를 해결하기 위해, L2R 및 R2L 로 훈련되는 두 가지의 독립적인 decoder 를 사용하는 연구가 있지만, 더 많은 파라미터와 긴 훈련 시간이 발생된다.

그러므로 bi-directional language modeling 으로 single decoder 를 채용하여 시도한다.

본 논문에서는 transformer decoder 를 사용하여 positional encoding 으로 인해 발생하는 coverage 부족 문제를 완화한다.

또한 새로운 bidirectional 훈련 기법으로 Bidirectionally Trained TRansformer (BTTR) 을 제안한다.

이 전략은 L2R 및 R2L 두 가지를 single transformer decoder 만으로 가능하다.

HMER task 에서 transformer 를 처음 시도
image 와 word positional encoding 의 결합을 input image 의 다양한 영역에 대한 attention 을 정확하게 align 하는 것을 각 단계마다 가능하여, coverage 무족 문제를 완화
bidirectional training 전략으로 single transformer decoder 만으로 bidirectional language modeling 가능
논문 게시 당시 CROHME 2014, 2016, 2019 에 SOTA
github : https://github.com/Green-Wood/BTTR

3 Methodology

3.1. CNN Encoder

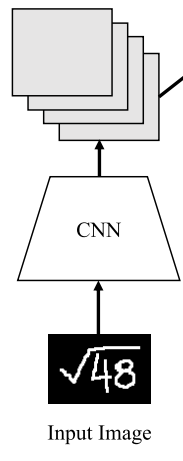
Encoder part

feature extractor 로 DenseNet 을 사용

각 layer 및 모든 subsequent layer 간의 직접적인 연결로 layer 간의 information flow 를 증가시킴
$0^{th}$ 부터 $(l-1)^{th}$ layer 의 output feature $x_0, x_1, \cdots, x_{l-1}$ 가 주어지면, $l^{th}$ layer 의 output feature 를 다음과 같이 계산

x_l = H_l([x_0; x_1; \cdots;x_{l-1}]) \tag{1}

$[x_0; x_1; \cdots;x_{l-1}]$ 는 모든 output feature 의 연결
$H(\cdot)$ 은 세 가지의 연속 layer 를 연결한 composite funtion
- batch normalization (BN)
- ReLU
- 3x3 convolution (Conv)

channel dimension 에 연결 작업으로 DenseNet 은 더 나은 gradient propagation 이 가능하며 ResNet 보다 더 적은 파라미터로 좋은 성능을 낼 수 있다.

추가적으로, DenseNet 에 1x1 convolution layer 를 추가하여 embedding dimension $d_{model}$ 의 사이즈를 조절한다.

3.2 Positional Encoding

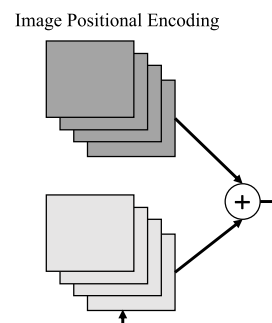
image feature 와 workd vectors 의 positional information 은 attend 가 필요한 region 을 식별하는데 도움이 된다.

RNN 베이스는 word vector 의 순서를 고려하기 때문에 image feature 의 positional information 을 무시한다.

본 논문에선 transformer 모델은 각 input vector 에 대한 어떠한 position 을 가지고 있지 않기 때문에, positional encoding 의 두 유형으로 해결한다.

image positional encoding
word positional encoding

image features 와 word features 를 content_based, 두 positional encoding 는 position-based 로 사용한다.

Word Positional Encoding

word positional encoding 은 transformer 연구에서 제안된 sinusoidal positional encoding 과 같다.

position $pos$ 와 dimension $d$ 가 input 으로 주어지면, word positional encoding vector $p^W_{pos, d}$ 는 다음과 같이 계산된다.

p^W_{pos, d}[2i] = \sin(pos/10000^{2i/d}) \tag{2}

p^W_{pos, d}[2i+1] = \cos(pos/10000^{2i/d}) \tag{3}

Image Positional Encoding

2-D normalized positional encoding 은 image position feature 표현에 사용된다.

먼저 두 dimensions 의 각각을 sinusoidal positional encoding $p^W_{pos,d/2}$ 를 계산한 후, 이들을 연결한다.

2-D position tuple $(x, y)$ 와, word positional encoding 와 동일한 dimension $d$ 가 주어지면, image positional encoding vector $P^I_{x,y,d}$ 는 다음과 같이 표현된다.

\bar{x} = \frac{x}{H},\ \bar{y} = \frac{y}{W} \tag{4}

P^I_{x,y,d} = [P^W_{\bar{x},d/2};p^W_{\bar{y},d/2}] \tag{5}

여기서 $H$ 와 $W$ 는 각각 input image 의 height 와 width 이다.

3.3 Transformer Decoder

Decoder part

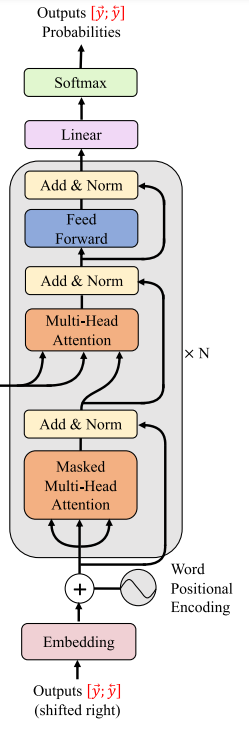
표준 transformer 를 사용하며, 4 가지 필수 파트를 포함한다.

Scaled Dot-Product Attention

attention 매커니즘은 query 와 key 간의 유사성을 기반으로 key-value 를 얻는 과정

Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V \tag{6}

Multi-Head Attention

multi-head 매커니즘은 query, key, value 를 subspace 에서 projection 하여 head $H$ 를 얻는 과정

$W^Q_i \in \mathbb{R}^{d_{model} \times d_k}$ , $W^K_i \in \mathbb{R}^{d_{model} \times d_k}$ , $W^V_i \in \mathbb{R}^{d_{model} \times d_v}$ 파라미터 행렬을 projection 한다.

H_i = Attention(QW^Q_i, KW^K_i, VW^V_i) \tag{7}

모든 head 는 연결되며 파라미터 행렬 $W^O \in \mathbb{R}^{hd_v \times d_{model}}$ 과 head 의 수 $h$ 로 projection 한다.

MultiHead(Q,K,V) = [H_1;...;H_h]W^O \tag{8}

Masked Multi-Head Attention

autoregressive 특성으로 인해, input image 와 이전 symbols 를 기반으로 다음 symbol 이 예측된다.

training 단계에서, triangle mask matrix 로 self-attention module 이 각 단계마다의 attention region 을 제한할 수 있다.

masked multi-head attention 매커니즘으로, 전체 훈련 과정 중 하나의 forward 계산만 필요해지게 된다.

Position-Wise Feed-Forward Network

Feed-Forward Network (FNN) 는 세 가지 연산을 포함

linear transformation
ReLU
another linear trnasforamation

FFN(x) = \max (0, xW_1 + b_1)W_2 + b_2 \tag{9}

multi-head attention 후, position 간의 information 은 전체적으로 exchange 된다. FFN 은 각 position 에서 내부 정보를 개별적으로 통합할 수 있다.

3.4 Bidirectional Training Strategy

먼저, 두 특별 symbol $\langle SOS \rangle$ 과 $\langle EOS \rangle$ 를 start 와 end sequence 로서 dictionary 에 도입한다.

target LaTeX sequence $y = \{ y_1, \cdots, y_T \}$ 의 경우, L2R 으로 부터의 target sequence 는 $\overrightarrow{y} = \{ \langle SOS \rangle, y_1, \cdots, y_T, \langle EOS \rangle \}$ , R2L 으로 부터의 target sequence 는 $\overrightarrow{y} = \{ \langle EOS \rangle, y_T, \cdots, y_1, \langle SOS \rangle \}$ 으로 나타낸다.

image $x$ 와 model parameter $\theta$ 에 따라 조정되며, 일반적인 autoregressive model 은 다음 확률 분포를 계산한다.

p(\overrightarrow{y}_j | \overrightarrow{y}_{<j},x,\theta) \tag{10}

여기서 j 는 target sequence 의 index 이다.

본 논문의 transformer model 은 input symbol 의 순서를 고려하지 않기 때문에, bidirectional language modeling 에 대한 single transformer decoder 를 사용할 수 있다.

다음 식과 Eq. (10) 을 동시에 모델링 한다.

p(\overleftarrow{y}_j | \overleftarrow{y}_{<j},x,\theta) \tag{11}

이렇게 생성된 두 target sequence, L2R 및 R2L 으로 training loss 를 계산한다.

비교를 위해 unidirectional language model 또한 훈련시킨다.

4 Implementation Details

4.1 Networks

encoder part

feature extractor 인 DenseNet 은 이전 SOTA method 인 DenseWAP 와 동일하게 사용

특히, 3 개의 bottleneck layer 를 backbone network 에 사용되며, transition layer 는 feature-map 수를 줄이기 위해 사이에 추가

growth rate : $k = 24$
각 block 의 depth : $D = 16$
transition layer 의 compression hyperparameter : $\theta = 0.5$

decoder part

표준 transformer 모델 사용

embedded dimension 과 model dimension : $d_{model} = 256$
multi-head attention 의 head 수 : $H = 8$
FFN 의 중간 층의 dimension : $d_{ff} = 1024$
transformer decoder layer 의 수 : $N = 3$
dropout rate : $0.3$

4.2 Training

Training 목표는 Eq. (10) 과 Eq. (11) 의 ground truth 예측 확률을 최소화하는 것이므로 표준 cross-entropy loss function 을 사용한다.

training sample $\{ x^{(z)}, y^{(z)} \}^Z_{z=1}$ 가 주어졌을 때 optimization 은 다음과 같다.

\overrightarrow{\mathcal{L}}^{(z)}_j(\theta) = -\log p(\overrightarrow{y}^{(z)}_j|\overrightarrow{y}^{(z)}_{<j}, x^{(z)}, \theta) \tag{12}

\overleftarrow{\mathcal{L}}^{(z)}_j(\theta) = -\log p(\overleftarrow{y}^{(z)}_j|\overleftarrow{y}^{(z)}_{<j}, x^{(z)}, \theta) \tag{13}

\mathcal{L}(\theta) = \frac{1}{2ZL}\sum^Z_{z=1}\sum^L_{j=1}(\overrightarrow{\mathcal{L}}^{(z)}_j(\theta) + \overleftarrow{\mathcal{L}}^{(z)}_j(\theta)) \tag{14}

Adadelta 사용
weight decay $10^{-4}$ , $\rho = 0.9$ , $\epsilon = 10^{-6}$

4.3 Inferencing

추론 과정에선, LaTeX sequence 생성을 위해 다음 공식을 사용한다.

\hat{y} = \underset{y}{\argmax} \ p(y|x,\theta) \tag{15}

ground-truth 이 없으므로 "End" symbol 이 나타나거나 정의된 최대 길이까지 symbol 을 하나씩 예측해야 한다.

모든 sequence 를 탐색하기 힘드므로 beam search 를 사용한다.

또한 decoder 가 양방향 모델링의 이점을 개선하기 윟 approximate joint search 를 사용하며 이 아이디어는 다음 세 단계로 구성된다.

L2R, R2L 에서 bean search 를 수행하여 두 개의 k-best 가설을 얻는다.
L2R 가설을 R2L 방향으로, R2L 가설을 L2R 방향으로 반전시키고, 이 가설들을 ground-truth 로 취급하여 훈련 단계처럼 각각의 손실 값을 계산
이 손실 값을 원래의 가설 점수에 추가하여 최종 점수를 얻은 후, 최적의 후보를 찾기 위해 사용

beam 크기 $k = 10$
최대 길이 $200$
length 패널티를 $\alpha = 1.0$

5 Experiments

Study

이전 포스트

Handwritten Mathematical Expression Recognition with Bidirectionally Trained Transformer

AI

Abstract

1 Introduction

3 Methodology

3.1. CNN Encoder