1. Introduction & 2. Related Works

• 이전의 2D to 3D generation

  • Triplane-base Transformer를 사용
  • 그러나 백본 모델의 연산량이 많아 모델 생성에 시간이 많이 걸림.
  • 이를 해결하기 위해 low resolution 이미지만을 학습시킴.
  • 하지만 저해상도 이미지 때문에 텍스처와 형상의 디테일이 많이 떨어짐.

• 저자들의 제안

  • 위 문제를 해결하기 위해 3D 가우시안을 활용
  • 이는 NeRF 기반의 볼륨 렌더링이나 Triplane-base 트랜스포머 기반의 모델보다 연산량이 적어 훨씬 빠름.
  • 또한 가우시안 하나가 밀도와 색상, 형상 등의 다양한 정보를 담고 있어 활용하기 쉬움.
  • 때문에 가우시안을 활용하면 적은 시간에 고해상도 이미지를 생성 가능.
  • 백본 모델의 연산량을 줄이기 위해 트랜스포머가 아닌 U-Net 기반의 모델을 설계.
  • 앞, 뒤, 옆 4장의 sparse한 이미지만으로 3D 오브젝트를 생성하기 위해선 고성능 피처 추출 모델이 필요함.
  • 저자들은 트랜스포머모다 가벼운 U-Net 기반의 백본 모델을 설계
  • U-Net 또한 가볍기 때문에 빠른 시간 내에 고해상도 3D 모델을 생성 가능
  • 모델 내부에는 어텐션 모듈이 삽입되어 각 시점의 이미지를 조합해 가우시안을 표현

• Data Augmentation 방식

  • 모델 훈련시에는 실제 3D 메쉬를 렌더링한 GT 이미지를 사용
  • 모델 추론시에는 디퓨전 모델을 통해 생성된 4시점 이미지들을 사용
  • 디퓨전 모델이 만들어낸 4시점 이미지들간에는 불일치가 존재하므로 GT와의 도메인 갭 발생
  • 이를 해결하기 위해, 이미지를 격자 기반으로 왜곡시킴
  • 또한 측면, 후면 이미지 카메라 각도에 추가 회전을 주어 robust 강화

• Mesh Extraction method

  • U-Net 기반의 피처맵의 한 픽셀 당 하나의 가우시안만을 생성하기 때문에, 이 결과로 메쉬를 추출하면 매우 saparse해지는 문제가 발생.
  • 따라서 해당 가우시안을 여러 각도에서 2D 이미지로 렌더링한 후, 이를 Instant NeRF 모델에 입력하여 볼륨 렌더링 결과를 생성.
  • 이 결과를 기반으로 메쉬를 생성하는 기법을 사용.

3. Method

3.1 Preliminaries

Large Multi-View Gaussian Model(LGM)의 핵심 구성 요소를 이해하는 데 필요한 두 가지 주요 사전 지식인 Gaussian Splatting과 Multi-View Diffusion Models에 대해 설명합니다.

• Gaussian Splatting (3D Gaussian Splatting)

  • 3D Gaussian Splatting은 3D Gaussian Splatting for Real-Time Radiance Field Rendering에서 소개된 3D 데이터를 표현하는 방식입니다.
  • 각 Gaussian은 3D 공간의 작은 타원형 블롭(ellipsoidal blob)으로 생각할 수 있습니다.
  • 이러한 각 Gaussian은 다음의 파라미터로 정의됩니다:
    • 중심 $\mathbf{x} \in \mathbb{R}^3$: 3차원 공간에서의 위치를 나타냅니다.
    • 스케일링 인자 $\mathbf{s} \in \mathbb{R}^3$: Gaussian의 크기(장축, 단축 길이)를 결정합니다.
    • 회전 쿼터니언 $\mathbf{q} \in \mathbb{R}^4$: Gaussian의 3차원 공간 내에서의 방향(orientation)을 나타냅니다.
    • 불투명도 $\alpha \in \mathbb{R}$: Gaussian이 얼마나 투명한지를 나타내는 값입니다.
    • 색상 특징 $\mathbf{c} \in \mathbb{R}^C$: Gaussian의 색상을 나타내며, 구형 고조파(spherical harmonics)를 사용하여 시점(view-dependent effects)에 따라 색상이 다르게 보이도록 모델링할 수 있습니다.
  • 렌더링 과정에서는 이러한 3D Gaussian들을 이미지 평면에 2D Gaussian으로 투영하고, 깊이 순서대로 알파 합성(alpha composition)을 수행하여 최종 픽셀의 색상과 불투명도를 결정합니다.
  • 이러한 표현 방식은 씬(scene)을 효과적으로 표현할 수 있는 뛰어난 표현력과 효율적인 렌더링 속도 때문에 3D 생성 분야에서 주목받고 있습니다.

• Multi-View Diffusion Models

  • 기존의 2D Diffusion Model은 주로 단일 시점 이미지 생성에 초점을 맞추었으며 3D 시점 조작을 지원하지 않습니다.
  • 최근 연구들 Sweetdreamer, Wonder3D, Zero123++, MVDream, ImageDream는 카메라 포즈를 추가 입력으로 통합하기 위해 3D 데이터셋에서 Multi-View Diffusion Model을 Fine-tuning할 것을 제안했습니다.
  • 이러한 접근 방식은 텍스트 프롬프트나 단일 시점 이미지를 통해 동일한 객체의 다양한 시점 이미지를 생성할 수 있게 합니다.
  • 그러나 실제 3D 모델이 없기 때문에 생성된 뷰들 간에 불일치(inconsistencies)가 여전히 발생할 수 있습니다.

이 논문 LGM은 Gaussian Splatting을 효율적인 3D 표현으로 활용하고, Multi-View Diffusion Model을 통해 생성된 다중 시점 이미지를 입력으로 받아 고해상도 3D 콘텐츠를 생성하는 새로운 프레임워크를 제시합니다. 이는 기존의 3D 생성 모델들이 겪었던 해상도 제약과 계산 부담 문제를 해결하고자 합니다.

3.2 Overall Framework

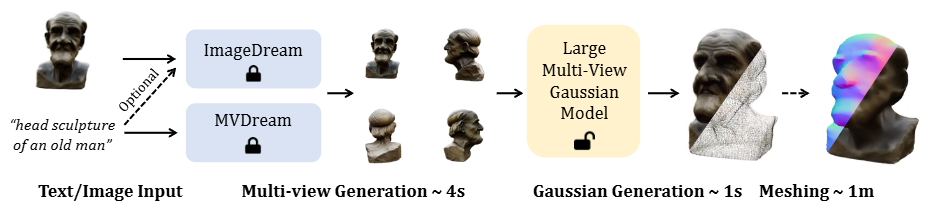
위 이미지는 LGM (Large Multi-View Gaussian Model)의 전체 3D 콘텐츠 생성 파이프라인을 보여줍니다. 텍스트 프롬프트나 단일 이미지 입력부터 고해상도 3D Gaussian을 생성하고, 선택적으로 메시(mesh)로 변환하는 과정을 단계별로 설명합니다.

• 텍스트/이미지 입력:

  • 사용자는 "head sculpture of an old man"과 같은 텍스트 프롬프트나 노인 흉상과 같은 단일 이미지를 시스템에 입력합니다.
  • 이 입력은 3D 모델 생성 과정의 시작점 역할을 합니다.

• 멀티뷰 생성 (Multi-view Generation) (약 4초 소요):

  • 이 단계에서는 ImageDream [51] (이미지 입력 시) 또는 MVDream [44] (텍스트 입력 시)과 같은 기존의 멀티뷰 Diffusion 모델이 사용됩니다.
  • 이 모델들은 입력받은 텍스트나 단일 이미지를 바탕으로 동일한 객체의 여러 시점(여기서는 4개) 이미지를 생성합니다.
  • 생성된 멀티뷰 이미지들은 실제 3D 객체에서 렌더링된 이미지와 약간의 차이(domain gap)나 시점 간 불일치(3D inconsistency)를 가질 수 있습니다. LGM 논문에서는 이러한 문제를 해결하기 위해 훈련 시 Grid Distortion 및 Orbital Camera Jitter와 같은 데이터 증강(data augmentation) 기법을 적용하여 모델의 견고성(robustness)을 높입니다.

• Gaussian 생성 (Large Multi-View Gaussian Model) (약 1초 소요):

  • 앞서 생성된 4개의 멀티뷰 이미지와 각 이미지에 해당하는 카메라 포즈 정보(Plücker ray embedding)가 Large Multi-View Gaussian Model의 입력으로 사용됩니다. 카메라 포즈 정보는 각 픽셀의 RGB 값, Ray Direction, Ray Origin × Ray Direction을 포함하는 9채널 특징 맵($f_i = \{c_i, o_i \times d_i, d_i\}$)으로 인코딩됩니다.
  • 이 모델의 핵심은 비대칭 U-Net(Asymmetric U-Net) 아키텍처입니다. 이 U-Net은 Residual Layers와 여러 뷰 간의 정보 공유를 위한 Cross-view Self-Attention Layers를 포함합니다.
  • U-Net의 출력 특징 맵의 각 픽셀은 하나의 3D Gaussian으로 해석됩니다. LGM은 입력 해상도(예: 256x256)보다 작은 출력 해상도(예: 128x128)를 가지는 비대칭 U-Net을 사용하여 고해상도 입력 이미지를 처리하면서도 최종 3D Gaussian의 수를 효율적으로 제어합니다 (총 128 x 128 x 4 = 65,536개의 Gaussian).
  • 생성된 3D Gaussian들은 미분 가능한 렌더링(differentiable rendering)을 통해 새로운 시점의 이미지로 렌더링되며, 이는 Ground Truth 이미지와의 비교를 통해 네트워크 훈련에 사용됩니다.

• 메싱 (Meshing) (선택 사항, 약 1분 소요):

  • 생성된 3D Gaussian들은 필요에 따라 폴리곤 메시(polygonal meshes)로 변환될 수 있습니다. 이는 게임 엔진이나 3D 그래픽 소프트웨어와 같은 후속 작업에서 메시 형식이 더 보편적으로 사용되기 때문입니다.
  • LGM의 메싱 과정은 직접 변환하는 대신 중간 단계를 거칩니다.
    • 먼저, 생성된 3D Gaussian들에서 렌더링된 이미지를 사용하여 NeRF (Neural Radiance Fields) [34]를 효율적으로 학습시킵니다. 이 과정에서는 형상(geometry)과 외형(appearance)을 재구성하기 위해 해시 그리드(hash grids)가 활용됩니다.
    • 다음으로, Marching Cubes [28] 알고리즘을 적용하여 초기 메시를 추출합니다. 이 메시는 미분 가능한 렌더링(differentiable rendering)을 통해 외형 해시 그리드와 함께 반복적으로 정제됩니다.
    • 마지막으로, 정제된 메시 위에 외형 필드를 베이킹(bake)하여 텍스처 이미지를 추출합니다. 이 간접적인 접근 방식은 덜 조밀한 Gaussian에서도 부드러운 표면과 상세한 텍스처를 가진 메시를 생성할 수 있도록 돕습니다.

3.3 Asymmetric U-Net for 3D Gaussians

본 논문에서 '비대칭 U-Net'은 LGM(Large Multi-View Gaussian Model) 프레임워크의 핵심 구성 요소로, 여러 시점의 이미지로부터 3D 가우시안(3D Gaussians)을 예측하고 융합하는 역할을 합니다.

• 목표: 고해상도 3D 생성을 위해 효율적인 3D 표현(representation)과 고해상도 훈련 능력을 동시에 달성하는 것입니다.
• 입력 및 출력:
  • 입력: 카메라 포즈 임베딩(camera pose embeddings)이 적용된 4개의 다중 시점 이미지($256 \times 256$ 해상도). 각 픽셀의 RGB 값과 해당 픽셀로부터 나아가는 광선에 대한 Plücker ray embedding 정보를 연결하여 9채널 특징 맵($f_i = \{c_i, o_i \times d_i, d_i\}$)으로 표현합니다. 여기서 $c_i$는 RGB 값, $d_i$는 광선 방향, $o_i$는 광선 원점입니다.
  • 출력: 4세트의 3D 가우시안을 표현하는 4개의 특징 맵($128 \times 128$ 해상도)으로, 각 픽셀이 하나의 3D 가우시안을 의미합니다. 최종적으로 이 가우시안들은 융합되어 완성된 3D 가우시안 모델이 됩니다.
• 아키텍처 설계:
  • U-Net 구조: 잔차 레이어(residual layers)와 셀프 어텐션(self-attention) 레이어로 구성된 비대칭 U-Net을 사용합니다.
  • 비대칭성: 입력 이미지 해상도($256 \times 256$)보다 작은 출력 해상도($128 \times 128$)를 가짐으로써, 높은 해상도의 입력 이미지를 처리하면서도 출력 가우시안의 수를 제한할 수 있습니다 (총 $128 \times 128 \times 4 = 65,536$개의 가우시안).
  • 교차 시점 셀프 어텐션(Cross-view Self-Attention): 여러 시점 간 정보 공유를 위해 U-Net의 깊은 레이어에 어텐션 블록이 통합되어 있습니다. 이는 4개의 이미지 특징을 평탄화(flatten)하고 연결(concat)한 후 셀프 어텐션을 적용하여 구현됩니다.
  • 가우시안 매개변수 예측: 출력 특징 맵의 각 픽셀은 3D 가우시안의 매개변수 $\Theta_i = \{x_i, s_i, q_i, \alpha_i, c_i\}$에 해당하는 14개의 채널을 가집니다. $x_i$는 중심(center), $s_i$는 스케일링 인자(scaling factor), $q_i$는 회전 쿼터니언(rotation quaternion), $\alpha_i$는 불투명도(opacity), $c_i$는 색상 특징(color feature)입니다.
  • 안정화 기법: 훈련 안정화를 위해 예측된 위치 $x_i$는 $[-1, 1]^3$으로 클램프(clamp)하고, Softplus 활성화된 스케일 $s_i$에 0.1을 곱하여 훈련 초기에 생성된 가우시안이 씬(장면)의 중앙에 가깝게 위치하도록 조정합니다.
• 선택 동기:
  • 효율적인 3D 표현: 3D 가우시안 스플래팅(3D Gaussian Splatting)은 단일 트라이플레인(triplane)에 비해 장면을 컴팩트하게 표현하는 표현력과 무거운 볼륨 렌더링(volume rendering)에 비해 렌더링 효율성이 뛰어나 고해상도 훈련에 용이합니다.
  • 고처리량 백본(High-throughput backbone): U-Net은 다중 시점 픽셀로부터 충분한 수의 가우시안을 효과적으로 생성할 수 있어 고해상도 훈련 역량을 유지합니다.

이 비대칭 U-Net 설계는 기존 LRM(Large Reconstruction Model) [15] 등에서 사용된 트라이플레인 기반 NeRF(Neural Radiance Field) [32] 및 트랜스포머(transformer) [15] 방식의 비효율적인 3D 표현과 과도한 매개변수화된 백본 문제를 해결하여 고해상도 3D 콘텐츠 생성의 병목 현상을 극복합니다.

3.3.1 피처맵의 픽셀 당 하나의 가우시안만 생성

원래 가우시안 논문은 픽셀로부터 시작되는 광선을 쏜 다음, 이 광선이 통과하는 다수의 가우시안들을 가중합해서 RGB를 렌더링합니다. 그런데 본 논문에서는 피처맵의 픽셀 하나 당 단 하나의 가우시안만 생성합니다. 이렇게 할 경우 가우시안이 너무 sparse해질 우려가 있습니다. 따라서 이 논문은 가우시안의 '개수'를 확보하기 위해 다음 두 가지 핵심 전략을 사용합니다.

• 1. 멀티뷰(Multi-View) 이미지 활용 및 가우시안 통합:

  • LGM의 핵심 아이디어는 단일 이미지에서 가우시안을 생성하는 것이 아니라, 4개의 다른 시점(view)에서 얻은 입력 이미지를 활용한다는 점입니다.
  • LGM의 비대칭 U-Net은 입력 이미지(256x256 해상도)를 처리하여 각 입력 시점마다 128x128 해상도의 출력 Gaussian feature map을 생성합니다. 그리고 이 4개의 시점에서 생성된 모든 가우시안들을 단순히 하나로 합칩니다.
  • 따라서 최종적으로 생성되는 3D Gaussian의 총 개수는 $128 \times 128 \times 4 = 65,536$개에 달합니다. 이는 단일 뷰에서 예측되는 픽셀 수(128x128 = 16,384)보다 4배 많은 숫자입니다. 즉 한 점을 4개의 투영된 이미지로부터 생성된 4개의 가우시안으로 표현하는 것입니다. 이 방법은 3D 객체를 표현하기에 충분히 많은 수의 가우시안을 확보할 수 있게 합니다.

• 2. Gaussian Splatting의 "표현력(Expressiveness)" 활용:

  • 논문에서 언급하듯이, Gaussian Splatting은 "단일 Triplane에 비해 장면을 압축적으로 표현하는 표현력이 뛰어나다"는 장점을 가지고 있습니다.
  • 즉, 각 3D Gaussian은 단순한 점이 아니라, scaling factor ($s_i \in \mathbb{R}^3$)와 rotation quaternion ($q_i \in \mathbb{R}^4$)을 통해 3차원 공간에서 크기와 방향을 가지는 타원체(ellipsoid) 형태로 존재하며, opacity($\alpha_i \in \mathbb{R}$)와 color feature($c_i \in \mathbb{R}^C$)를 포함합니다. 이처럼 풍부한 파라미터 덕분에, 상대적으로 적은 수의 가우시안으로도 복잡한 3D 디테일과 외관을 효과적으로 나타낼 수 있습니다.
  • 이 논문은 기존의 Triplane 기반 NeRF 방식이 저해상도 훈련에 제약이 있었던 문제점을 지적하며, Gaussian Splatting의 이러한 표현력과 효율적인 렌더링(3D Gaussian Splatting for Real-Time Radiance Field Rendering)이 고해상도 3D 생성을 가능하게 한다고 주장합니다.

• LGM은 출력 feature map의 한 픽셀 당 하나의 Gaussian을 예측하지만, 이를 4개의 시점에서 수행하고 그 결과를 결합함으로써 충분한 수의 3D Gaussian을 확보합니다. 또한, 3D Gaussian 자체가 가진 뛰어난 표현력 덕분에 각 가우시안이 3D 공간에서 차지하는 정보량이 많아, 그 개수가 적더라도 전체적으로 3D 모델의 디테일과 품질을 높일 수 있습니다.

• 다만, 논문 8페이지 "3.5 Mesh Extraction"과 19페이지 "Limitations"에서 언급된 한계점도 있습니다. LGM이 생성한 가우시안은 렌더링에는 적합하지만, 폴리곤 메시(polygonal mesh) 추출 시에는 "sparse"하여 표면에 구멍이 생길 수 있다고 밝힙니다. 이 문제를 해결하기 위해 별도의 메시 추출 파이프라인(NeRF를 중간 단계로 활용)을 제안합니다. 이는 렌더링을 위한 가우시안 분포와 직접적인 메시 변환을 위한 가우시안 분포 사이에 여전히 차이가 있을 수 있음을 시사합니다.

3.3.2 Plücker ray embedding

Plücker ray embedding은 3D 공간에서 광선(ray) 또는 직선(line)을 표현하는 효율적인 방법 중 하나입니다. 이는 기하학적 정보를 벡터 형태로 인코딩하여 신경망 모델이 3D 기하학적 관계를 이해하고 처리하는 데 도움을 줍니다. 공식은 다음과 같습니다:

각 항의 의미는 다음과 같습니다:

• $f_i$: 픽셀 $i$에 대한 입력 특징(feature) 벡터입니다. 이 특징 벡터는 U-Net의 첫 번째 레이어에 입력되는 9채널 특징 맵을 구성합니다.
• $c_i$: 픽셀 $i$의 RGB 값입니다. 이는 이미지의 색상 정보를 나타내며 3개의 채널로 구성됩니다.
• $o_i$: 픽셀 $i$를 통과하는 카메라 광선(ray)의 원점(origin)입니다. 3D 공간에서의 카메라 위치와 관련된 정보를 담고 있습니다.
• $d_i$: 픽셀 $i$를 통과하는 카메라 광선의 방향(direction)입니다. 3D 공간에서의 광선 방향을 나타내며, 이는 픽셀이 바라보는 3D 공간의 지점을 결정하는 데 중요합니다.
• $o_i \times d_i$: 광선의 원점 $o_i$와 방향 $d_i$의 벡터 곱(cross product)입니다. 이 항은 Plücker ray embedding의 한 구성 요소로, 광선의 기하학적 정보를 인코딩합니다. 이 벡터 곱은 광선이 지나는 평면의 법선 벡터와 관련이 있어 3D 공간에서 광선의 위치와 방향을 고유하게 정의하는 데 도움을 줍니다. 이는 3개의 채널로 구성됩니다.

• 해당 임베딩의 장점
  • 기하학적 관계 처리 용이 (Ease of Handling Geometric Relations): 두 직선의 교차, 평행 여부, 최단 거리 등 다양한 기하학적 관계를 벡터 연산을 통해 효율적으로 계산할 수 있습니다.
  • 신경망 모델에 적합 (Suitability for Neural Networks): 6차원 벡터 형태로 광선의 기하학적 정보를 밀도 높게 인코딩하므로, 신경망이 광선의 3D 위치 및 방향을 효과적으로 학습하고 추론하는 데 용이합니다. 기존의 개별적인 카메라 파라미터(위치, 방향)를 사용하는 것보다 더욱 압축적이고 표현력이 뛰어납니다.

각 구성요소 분석

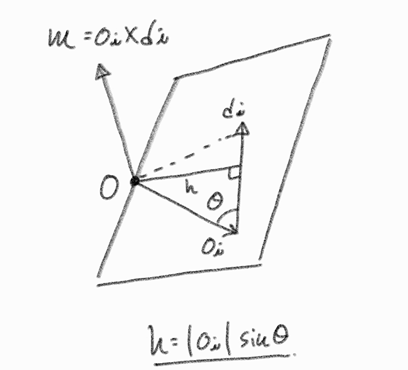
• $o_i \times d_i$는 광선과 원점을 포함하는 평면의 법선벡터

  • 벡터 외적(cross product)의 정의에 따르면, 두 벡터 $\mathbf{a}$와 $\mathbf{b}$의 외적 $\mathbf{a} \times \mathbf{b}$는 이 두 벡터 모두에 수직인 벡터를 생성합니다.
  • 광선은 점 $\mathbf{o}_i$ (카메라의 중심, 즉 광선의 원점)를 통과하여 방향 $\mathbf{d}_i$로 나아가는 반직선입니다.
  • 따라서 $\mathbf{o}_i$와 $\mathbf{d}_i$는 3D 공간에서 하나의 평면을 정의할 수 있습니다 (단, $\mathbf{o}_i$와 $\mathbf{d}_i$가 평행하지 않아야 함).
  • 이때, $\mathbf{o}_i \times \mathbf{d}_i$는 $\mathbf{o}_i$와 $\mathbf{d}_i$가 놓여 있는 평면의 법선 벡터(normal vector)가 됩니다.

• 모멘트 벡터 $\mathbf{m}$은 광선과 원점 사이의 거리와 회전 관계를 나타냄

  • 거리(Distance) 표현:

    • 모멘트 벡터 $\mathbf{m}$의 크기는 $|\mathbf{m}| = |\mathbf{o}_i \times \mathbf{d}_i| = |\mathbf{o}_i| |\mathbf{d}_i| \sin\theta$ 입니다. 여기서 $\theta$는 벡터 $\mathbf{o}_i$와 $\mathbf{d}_i$ 사이의 각도입니다.
    • 만약 방향 벡터 $\mathbf{d}_i$가 단위 벡터(크기가 1인 벡터, 즉 $|\mathbf{d}_i|=1$)라면, $|\mathbf{m}| = |\mathbf{o}_i| \sin\theta$가 됩니다.
    • 기하학적으로 $|\mathbf{o}_i| \sin\theta$는 원점(global origin)에서 광선이 정의하는 직선(line)까지의 수직 거리(perpendicular distance)와 같습니다. 즉, 원점과 광선 사이의 최단 거리입니다.
    • 따라서 $\mathbf{m}$의 크기는 광선이 3D 공간의 원점으로부터 얼마나 떨어져 있는지를 나타냅니다.

  • "회전" 관계 (Rotational Relationship) 표현:

    • $\mathbf{m}$의 방향은 $\mathbf{o}_i$와 $\mathbf{d}_i$ 모두에 수직입니다.
    • 이는 $\mathbf{m}$이 원점(global origin)과 광선을 모두 포함하는 평면의 법선 벡터라는 의미와 연결됩니다. 이 법선 벡터의 방향은 광선이 원점을 중심으로 어떻게 "기울어져" 있는지를 나타낸다고 볼 수 있습니다.
    • 예를 들어, 광선이 원점을 통과한다면 ($\mathbf{o}_i = \mathbf{0}$이거나 광선이 원점을 지나는 경우), 모멘트 벡터 $\mathbf{m}$은 $\mathbf{0}$이 됩니다. 이는 원점과 광선 사이의 거리가 0임을 의미하며, "회전" 관계도 없다고 볼 수 있습니다.
    • 반대로 광선이 원점으로부터 멀리 떨어져 있거나, 원점과의 상대적인 방향이 특정 "회전"을 나타낼 때, $\mathbf{m}$은 그 관계를 벡터의 방향과 크기로 인코딩합니다. 이는 광선의 "위치" 정보와 "방향" 정보가 결합되어 나타나는 효과입니다.

• $\mathbf{d} \cdot \mathbf{m} = \mathbf{d} \cdot (\mathbf{o} \times \mathbf{d}) = 0$ 이라는 특성이 3D 공간에서 광선을 고유하게 정의

  • 이 특성은 Plücker 관계(Plücker relation) 또는 직교성 조건(orthogonality condition)이라고 불립니다.
  • 벡터 외적의 속성: 벡터 외적 $\mathbf{o} \times \mathbf{d}$의 결과는 항상 원래의 두 벡터 $\mathbf{o}$와 $\mathbf{d}$ 모두에 수직입니다. 따라서 $\mathbf{m}$은 $\mathbf{d}$에 수직이므로, 두 벡터의 내적 $\mathbf{d} \cdot \mathbf{m}$은 반드시 0이 됩니다. 이는 수학적인 필연적인 결과입니다.
  • 자유도 감소 및 유효한 선 표현: 3D 공간에서 임의의 직선을 완전히 정의하려면 4개의 독립적인 매개변수가 필요합니다 (예: 두 점, 또는 한 점과 방향, 그리고 특정 제약 조건). 하지만 6차원 벡터 $(\mathbf{d}, \mathbf{m})$는 6개의 매개변수를 가집니다.
  • 이 6개의 매개변수가 실제로 하나의 유효한 직선(또는 광선)을 나타내려면, 두 가지 조건이 필요합니다.
    1. $\mathbf{d} \neq \mathbf{0}$: 방향 벡터가 0이 아니어야 합니다 (점과 직선은 다름).
    2. $\mathbf{d} \cdot \mathbf{m} = 0$: 이 Plücker 관계를 만족해야 합니다. 이 조건은 6차원 벡터 공간에서 2개의 제약(direction vector의 크기가 0이 아니어야 한다는 것과 orthogonality condition)을 가하여, 실제로 4개의 독립적인 자유도를 가진 직선을 정확히 표현하게 만듭니다.
  • "고유하게 정의": 이 관계가 없다면, 임의의 6차원 벡터 $(\mathbf{v}_1, \mathbf{v}_2)$가 주어졌을 때, 그것이 실제로 어떤 직선을 나타내는지 명확하지 않습니다. 예를 들어, $\mathbf{v}_2$가 $\mathbf{v}_1$에 수직이 아니라면, 이 쌍은 3D 공간에서 물리적인 의미의 직선을 나타낼 수 없습니다. Plücker 관계는 6차원 벡터가 유효한 3D 직선을 나타내기 위한 필수 조건이며, 이 조건을 만족하는 6차원 벡터만이 3D 직선을 고유하게 표현할 수 있습니다.
  • 이처럼 카메라 광선의 기하학적 정보를 명시적으로 포함한 정보를 $f_i = \{c_i, o_i \times d_i, d_i\}$와 같이 9채널 특징 맵으로 결합하여 전달함으로써, U-Net은 2D 이미지 특징뿐만 아니라 해당 픽셀이 3D 공간에서 어디에 위치하는지, 어떤 방향을 바라보는지에 대한 깊은 이해를 바탕으로 3D Gaussians를 예측할 수 있게 됩니다. 이는 특히 다중 뷰 이미지로부터 일관된 3D 모델을 생성하는 데 매우 중요합니다.

3.3.3 안정화 기법

LGM 모델의 학습 안정성을 위해 가우시안의 초기 위치와 크기를 제한하는 두 가지 주요 조정이 이루어집니다.

• 예측된 위치 $x_i$를 $[-1, 1]^3$ 범위로 클램프(Clamp)하는 것:

  • $x_i$는 $i$번째 3D 가우시안의 중심 위치를 나타냅니다.
  • 클램프는 특정 값을 주어진 최솟값과 최댓값 사이에 강제로 고정시키는 연산입니다.
  • 즉, 가우시안의 중심이 3D 공간에서 각 축의 좌표가 -1과 1 사이인 정육면체(cube) 영역($[-1, 1]^3$)을 벗어나지 않도록 합니다.
  • 목적: 학습 초기에 가우시안들이 무작위로 너무 넓은 공간에 퍼지는 것을 방지하여, 모델이 장면에 대한 초기 이해를 장면의 중심부에 집중하도록 돕고 학습의 안정성을 높입니다.

• softplus 활성화 함수가 적용된 스케일 $s_i$에 0.1을 곱하는 것:

  • $s_i$는 $i$번째 3D 가우시안의 스케일(크기)을 나타냅니다. 이는 가우시안의 3D 형태와 영향을 미치는 범위를 결정합니다.
  • softplus는 입력값이 어떤 값이든 항상 양수 값을 출력하는 활성화 함수입니다. 스케일은 물리적인 크기를 나타내므로 음수가 될 수 없기 때문에, softplus를 사용하여 항상 양수를 보장합니다.
    • Softplus 함수: $\text{softplus}(x) = \ln(1 + e^x)$
  • 이렇게 softplus를 적용한 스케일 값에 추가적으로 0.1을 곱하여 가우시안의 초기 크기를 매우 작게 제한합니다.
  • 목적: 학습 초기에 가우시안들이 너무 커서 장면의 세부 정보를 표현하지 못하거나, 불필요하게 넓은 영역에 영향을 미치는 것을 방지합니다. 작은 크기로 시작함으로써 모델이 세밀한 3D 구조와 텍스처를 점진적으로 학습할 수 있는 환경을 조성합니다.

이러한 조정은 3D Gaussian Splatting [17] 모델의 학습 초기 단계에서 가우시안들이 장면의 중심 영역에 밀집되어 작고 안정적인 형태로 존재하도록 보장함으로써, 전체적인 학습 과정의 안정성과 효율성을 크게 향상시킵니다. 이는 Gaussian Splatting이 높은 렌더링 효율성을 가지지만, 3D 가우시안의 수와 파라미터가 충분히 많아야 디테일한 3D 정보를 정확하게 표현할 수 있다는 점을 고려할 때 중요한 전략입니다.

3.4 Robust Training

LGM 모델의 강건한 학습 (robust training)을 위해 사용된 데이터 증강 기법과 손실 함수에 대해 설명합니다. 여기서 LGM은 대규모 Objaverse [12] 데이터셋에서 렌더링된 다중 뷰 이미지를 활용하여 3D 재구성 모델을 학습시킵니다. 또한, 추론 단계에서는 MVDream [14]이나 ImageDream [51]과 같은 최신 다중 뷰 확산 모델을 활용하여 텍스트나 단일 이미지를 다중 뷰 이미지로 변환하고, 이를 LGM의 입력으로 사용하여 3D 콘텐츠를 생성합니다.

• 데이터 증강 (Data Augmentation)

  • 목적: 학습에 사용되는 실제 3D 객체에서 렌더링된 다중 뷰 이미지 [📄 Objaverse]와 추론 시 다중 뷰 확산 모델 (MVDream, ImageDream 등)을 통해 합성된 이미지 사이의 도메인 간극 (domain gap)을 줄여 모델의 강건함을 높이는 데 초점을 맞춥니다.
  • 그리드 왜곡 (Grid Distortion):
    • 설명: 주로 정면 참조 뷰(첫 번째 입력 뷰)를 제외한 나머지 세 개의 입력 뷰에 무작위 그리드 왜곡을 적용합니다.
    • 효과: 이는 다중 뷰 확산 모델이 생성하는 이미지 간의 미묘한 불일치(inconsistency)를 시뮬레이션하여, 모델이 이러한 불일치에 더욱 강건하게 반응하도록 돕습니다.
  • 궤도 카메라 지터 (Orbital Camera Jitter):
    • 설명: 입력 이미지의 카메라 포즈(자세)가 정확하지 않을 수 있음을 시뮬레이션하기 위해, 첫 번째 뷰를 제외한 나머지 세 개의 입력 뷰에 대해 카메라 포즈를 씬 중심 주위로 무작위로 회전시킵니다.
    • 효과: 모델이 부정확한 카메라 포즈와 레이 임베딩(ray embedding)에 더 잘 견디도록 만듭니다.

• 손실 함수 (Loss Function)

  • 모델은 미분 가능한 렌더러를 사용하여 3D 가우시안을 새로운 뷰(novel view)로 렌더링하고, 이 렌더링된 이미지와 실제 이미지 (ground truth image) 간의 차이를 줄이는 방식으로 학습됩니다.
  • RGB 이미지 손실 ($L_{rgb}$): 렌더링된 RGB 이미지와 실제 RGB 이미지 간의 차이를 계산합니다.
    • 평균 제곱 오차 (MSE)와 LPIPS 손실의 조합으로 구성됩니다.
    • 식: $L_{rgb} = L_{MSE}(I_{rgb}, I^{GT}_{rgb}) + \lambda L_{LPIPS}(I_{rgb}, I^{GT}_{rgb})$
      • $I_{rgb}$: 렌더링된 RGB 이미지
      • $I^{GT}_{rgb}$: 실제 RGB 이미지
      • $L_{MSE}$: 평균 제곱 오차 (픽셀 값의 직접적인 차이 측정)
      • $L_{LPIPS}$: LPIPS 손실 (perceptual loss라고도 불리며, 사람의 시각적 인지에 더 가깝게 이미지 유사성을 측정)
      • $\lambda$: LPIPS 손실의 가중치
  • 알파 이미지 손실 ($L_{\alpha}$): 렌더링된 알파 이미지 (투명도 정보)와 실제 알파 이미지 간의 평균 제곱 오차 (MSE)를 적용합니다.
    • 식: $L_{\alpha} = L_{MSE}(I_{\alpha}, I^{GT}_{\alpha})$
      • $I_{\alpha}$: 렌더링된 알파 이미지
      • $I^{GT}_{\alpha}$: 실제 알파 이미지
    • 효과: 이는 형상(shape)의 더 빠른 수렴을 돕습니다.

미분 가능한 렌더링 (Differentiable Rendering)
3D 장면을 2D 이미지로 렌더링하는 과정이 미분 가능하도록 설계된 기술을 의미합니다. 이는 렌더링된 2D 이미지와 실제(ground truth) 2D 이미지 간의 차이를 줄이기 위해 역전파 (backpropagation)를 통해 3D 장면의 파라미터(예: 형상, 재질, 조명, 3D 가우시안 파라미터 등)를 직접 최적화할 수 있도록 합니다.

• 기존 렌더링의 한계: 전통적인 컴퓨터 그래픽스 렌더링은 3D 모델에서 2D 이미지를 생성하는 단방향 과정입니다. 이 과정은 일반적으로 미분 불가능한 단계(예: 가시성 결정, 픽셀에 대한 이산적인 결정 등)를 포함하여, 2D 이미지에서 3D 장면의 파라미터를 역으로 추론하거나 최적화하기 어렵습니다.
• 역전파 가능성: 미분 가능한 렌더링은 렌더링 파이프라인의 모든 단계가 미분 가능하도록 재구성합니다. 이를 통해 렌더링된 픽셀 값이 3D 장면을 구성하는 파라미터(예: 정점 좌표, 텍스처 색상, 카메라 자세, 3D 가우시안의 위치/크기/색상 등)에 대해 얼마나 민감하게 변하는지를 나타내는 그라디언트 (gradients)를 계산할 수 있습니다.
• 활용 목적:
  • 역문제 해결: 2D 이미지에서 3D 장면을 재구성하거나 3D 모델을 특정 목표에 맞게 생성하는 것과 같은 역문제 (inverse problems)를 풀 수 있게 합니다.
  • 최적화: 2D 이미지와 3D 모델 간의 오차를 손실 함수 (loss function)로 정의하고, 이 손실을 최소화하는 방향으로 3D 모델의 파라미터를 경사 하강법 (gradient descent)과 같은 최적화 알고리즘을 사용하여 업데이트할 수 있습니다.
  • 학습: 인공지능 모델이 3D 데이터를 직접 다루지 않고도 2D 이미지와의 비교를 통해 3D 개념을 학습할 수 있게 합니다.

작동 방식:

1. 3D 표현: 장면을 특정 3D 표현(예: 메시, NeRF [32], 3D 가우시안 [17] 등)으로 정의합니다.
2. 렌더링 함수: 이 3D 표현을 카메라 파라미터와 함께 미분 가능한 렌더링 함수에 입력하여 2D 이미지를 렌더링합니다. 이 함수는 투명도 혼합(alpha compositing)이나 부피 렌더링(volume rendering)과 같은 연속적인 연산을 사용하여 미분 가능성을 유지합니다. 즉, NeRF에 사용된 방식이 대표적인 미분 가능한 렌더링 방식입니다.
3. 손실 계산: 렌더링된 이미지와 실제 이미지를 비교하여 손실을 계산합니다.
4. 그라디언트 계산: 손실 함수에 대해 3D 장면 파라미터까지 역전파하여 그라디언트를 계산합니다. 이 그라디언트는 각 3D 파라미터를 어떤 방향으로 얼마나 업데이트해야 손실이 줄어드는지를 알려줍니다.
5. 파라미터 업데이트: 계산된 그라디언트를 사용하여 3D 파라미터를 업데이트하고, 이 과정을 반복하여 최적의 3D 장면을 찾습니다.

3.5 Mesh Extraction

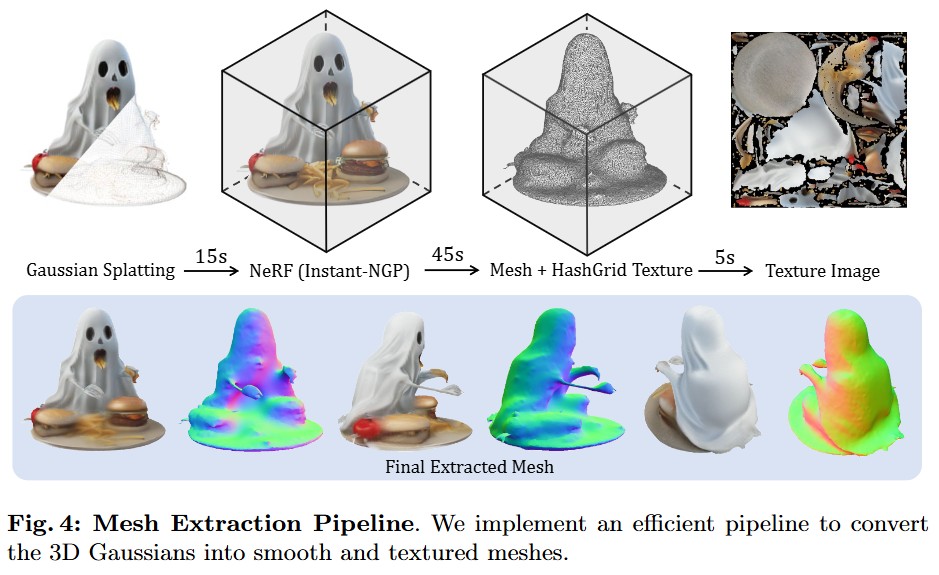
LGM 모델에서 생성된 3D 가우시안(Gaussians)을 다양한 하위 작업에 사용될 수 있는 폴리곤 메시(polygonal meshes)로 변환하는 방법에 대해 설명합니다.

• 메시 추출의 필요성: 폴리곤 메시는 디지털 게임, 가상 현실, 영화 제작 등 다양한 3D 작업에서 가장 널리 사용되는 3D 표현 방식입니다. LGM이 3D 가우시안을 생성하지만, 실제 응용을 위해서는 메시 형태로의 변환이 필요합니다.
• 기존 방법의 한계: 이전 연구(DreamGaussian)에서는 3D 가우시안의 불투명도(opacity) 값을 직접 점유 필드(occupancy field)로 변환하여 메시를 추출하려고 시도했습니다. 하지만 이 방법은 부드러운 점유 필드를 생성하기 위해 3D 가우시안을 공격적일 정도로 밀집화 해야 했습니다. 그러나 LGM에서 생성된 가우시안은 sparse하여 구멍이 있는 불만족스러운 표면을 생성하는 한계가 있었습니다.
• LGM의 메시 추출 파이프라인: LGM은 이러한 문제를 해결하기 위해 보다 일반적인 메시 추출 파이프라인을 제안합니다.
  • NeRF 학습: 먼저, 3D 가우시안에서 렌더링된 이미지를 실시간으로 활용하여 Instant NeRF(Instant neural graphics primitives with a multiresolution hash encoding)를 학습합니다. 두 개의 해시 그리드(hash grid)를 사용하여 기하학(geometry)과 외형(appearance)을 재구성합니다.
  • 초기 메시 추출: Marching Cubes(Marching cubes: A high resolution 3d surface construction algorithm) 알고리즘을 적용하여 대략적인 메시를 추출합니다.
  • 해시 그리드 인코딩: 여러 해상도의 그리드에 학습 가능한 특징 벡터(feature vector)를 저장해두고, 3D 공간의 어떤 한 점을 쿼리할 때 이 그리드에서 특징을 보간(interpolation)하여 추출합니다. 이 특징들을 작은 신경망에 넣어 최종 색상과 밀도를 얻습니다. 이 때 NeRF가 학습하는 3D 형태와 외형(색상, 텍스처)을 각각 담당하는 해시 그리드를 분리하여 사용합니다.
  • 반복적인 정제: 추출된 대략적인 메시는 외형 해시 그리드와 함께 미분 가능한 렌더링(differentiable rendering)을 사용하여 반복적으로 최적화 됩니다.
  • 텍스처 추출: 최종적으로 정제된 메시에 외형 필드(appearance field)의 정보를 사용하여 텍스처 이미지(texture images)를 추출합니다.
• 효율성: 이러한 가우시안-NeRF-메시 변환 과정은 약 1분 이내에 완료되어 효율적이라고 언급하고 있습니다.

이 접근 방식은 DreamGaussian과 같이 3D 가우시안을 직접 메시로 변환하는 방식의 한계를 극복하고, 희소한 가우시안에서도 부드럽고 텍스처가 있는 메시를 얻을 수 있도록 함으로써 LGM의 활용도를 높입니다.

4. Experiments

4.1 Implementation Details

• 데이터셋 (Datasets)

  • 학습 데이터: Objaverse 데이터셋의 필터링된 하위 집합을 사용했습니다.
  • 데이터 필터링:
    • Cap3D [30]에서 캡션과 렌더링된 이미지를 수동으로 검사하여 'resembling', 'debris', 'frame'과 같이 품질이 낮은 모델에서 흔히 발견되는 단어를 포함하는 모델을 제외했습니다.
    • 렌더링 후 대부분 흰색 배경을 가진 모델은 누락된 텍스처를 나타내는 경우가 많아 제외했습니다.
  • 최종 데이터셋: 약 8만 개의 3D 객체로 구성됩니다.
  • 렌더링: 학습 및 검증을 위해 512 × 512 해상도로 100개의 카메라 뷰에서 RGBA 이미지를 렌더링했습니다.

• 네트워크 아키텍처 (Network Architecture)

  • U-Net 구조: 6개의 다운 블록, 1개의 미들 블록, 5개의 업 블록으로 구성된 비대칭 U-Net 모델을 사용합니다.
  • 입력 및 출력: 256 × 256 해상도의 입력 이미지를 받아 128 × 128 해상도의 Gaussian 특징 맵을 출력합니다.
  • Gaussian 개수: 4개의 입력 뷰를 사용하므로, 출력 Gaussian의 총 개수는 128 × 128 × 4 = 65,536개입니다.
  • 특징 채널: 각 블록의 특징 채널은 순서대로 [64, 128, 256, 512, 1024, 1024], [1024], [1024, 1024, 512, 256, 128]입니다.
  • 레이어 구성: 각 블록에는 일련의 Residual layers와 선택적인 Down-sample 또는 Up-sample layer가 포함됩니다.
  • Cross-view Self-Attention: 마지막 3개의 다운 블록, 미들 블록, 그리고 첫 3개의 업 블록에는 Residual layers 뒤에 Cross-view Self-Attention layers가 삽입됩니다.
  • 최종 특징 맵: 1x1 Convolution layer를 통해 14채널 픽셀 단위 Gaussian 특징으로 처리됩니다.
  • 활성화 함수 및 정규화: Silu 활성화 함수와 Group Normalization을 사용합니다.
  • Gaussian 파라미터: 예측된 위치 $x_i$는 $[-1, 1]^3$으로 클램프(clamp)되고, softplus-activated scales $s_i$는 0.1을 곱하여 초기 학습 시 Gaussian들이 장면 중앙에 가깝게 위치하도록 합니다.

• 학습 (Training)

  • 하드웨어: 32개의 NVIDIA A100 (80G) GPU에서 약 4일 동안 학습했습니다.
  • 배치 크기: 각 GPU당 8개의 배치 크기를 사용하며, bfloat16 정밀도로 총 256의 효과적인 배치 크기를 가집니다.
  • 카메라 뷰 샘플링: 각 배치에서 8개의 카메라 뷰를 무작위로 샘플링하며, 처음 4개 뷰는 입력으로, 8개 뷰는 모두 감독(supervision)을 위한 출력으로 사용됩니다.
  • 카메라 변환: LRM과 유사하게, 각 배치의 카메라를 변환하여 첫 번째 입력 뷰가 항상 정면 뷰가 되도록 고정했습니다.
  • 배경: 입력 이미지는 흰색 배경을 가진다고 가정했습니다.
  • 손실 함수 해상도: 출력 3D Gaussians는 Mean Square Error (MSE) Loss를 위해 512 × 512 해상도로 렌더링됩니다. LPIPS Loss를 위해 이미지는 256 × 256으로 크기가 조정됩니다.
  • 옵티마이저: AdamW [29] 옵티마이저를 사용했습니다.
  • 학습률: 학습률은 $4 \times 10^{-4}$이며, Weight Decay는 0.05, betas는 (0.9, 0.95)입니다. 학습률은 코사인 어닐링(cosine annealed) 방식으로 0까지 감소합니다.
  • 그래디언트 클리핑: 최대 노름(norm) 1.0으로 그래디언트를 클리핑합니다.
  • 데이터 증강 확률: Grid Distortion과 Camera Jitter의 확률은 50%로 설정했습니다.

• 추론 (Inference)

  • GPU 메모리: 전체 파이프라인(두 개의 Multi-view Diffusion Models 포함)은 추론 시 약 10GB의 GPU 메모리만 사용하므로 배포에 용이합니다.
  • Diffusion Model 설정:
    • ImageDream에는 Guidance Scale 5를, MVDream에는 7.5를 사용했습니다.
    • Diffusion Steps는 DDIM [45] 스케줄러를 사용하여 30으로 설정했습니다.
  • 카메라 뷰: 카메라 Elevation은 0으로 고정하고, Azimuth는 [0, 90, 180, 270]도로 4개의 생성된 뷰에 대해 설정했습니다.
  • ImageDream 입력: ImageDream [51]의 경우, 텍스트 프롬프트는 항상 비워두어 단일 이미지 입력만 사용하도록 했습니다.
  • 배경 처리: MVDream으로 생성된 이미지에는 다양한 배경이 포함될 수 있으므로, Background Removal [37]을 적용하여 흰색 배경을 사용했습니다.

• 코사인 어닐링(Cosine Annealing)
  학습률이 학습 에포크(epoch)나 배치(batch)의 진행에 따라 코사인 함수의 형태를 따르며 감소하고, 특정 시점마다 다시 초기 학습률로 돌아가거나 최소 학습률까지 떨어지는 것을 반복하는 방식입니다.
  이는 학습 초기에 비교적 큰 학습률로 빠르게 탐색하고, 학습이 진행될수록 학습률을 점진적으로 줄여 미세 조정하며 최적점에 안정적으로 수렴하도록 돕습니다.

  • 목적 (Purpose)

    • 더 나은 최적점 탐색: 학습률이 너무 크면 최적점을 건너뛸 수 있고, 너무 작으면 수렴 속도가 느려지거나 지역 최적점에 갇힐 수 있습니다. 코사인 어닐링은 이러한 문제를 완화하며 더 넓은 공간을 탐색하고 동시에 안정적인 수렴을 가능하게 합니다.
    • 지역 최적점 탈출: 학습률을 주기적으로 높였다가 다시 낮추는(리스타트) 방식으로, 모델이 지역 최적점(local optima)에 갇히는 것을 방지하고 전역 최적점(global optima)을 찾아낼 가능성을 높입니다.

  • 작동 방식 (How it Works)

    • 가장 기본적인 코사인 어닐링은 학습률이 최대값에서 시작하여 코사인 반주기(half-cycle)를 따라 최소값까지 감소합니다.
    • 수식으로 표현하면 다음과 같습니다. 각 에포크 $T_i$ 내에서 현재 에포크 $t$에서의 학습률 $η_t$는:
      $η_t = η_{min} + \frac{1}{2}(η_{max} - η_{min})\left(1 + \cos\left(\frac{t}{T_{cur}}\pi\right)\right)$
      • $η_t$: 현재 학습률
      • $η_{min}$: 최소 학습률 (보통 0에 가깝거나 0)
      • $η_{max}$: 최대 학습률 (초기 학습률)
      • $T_{cur}$: 현재 재시작 주기 내의 에포크 수 (또는 총 에포크 수)
      • $t$: 현재 에포크 인덱스
    • 이때, $T_{cur}$는 전체 학습 주기일 수도 있고, 여러 번 재시작하는 경우 하나의 주기 길이일 수도 있습니다. SGDR (Stochastic Gradient Descent with Warm Restarts)과 같은 변형에서는 학습률을 주기적으로 재시작하여 다시 큰 값으로 만들고, 이때 주기 $T_{cur}$를 점진적으로 늘리기도 합니다.

  • 장점 (Benefits)

    • 빠른 수렴: 초기에 큰 학습률로 빠른 탐색을 가능하게 합니다.
    • 안정적인 수렴: 후반부에 학습률을 낮춰 안정적인 미세 조정을 돕습니다.
    • 성능 향상: 지역 최적점에 덜 갇히고 더 나은 일반화 성능을 보이는 경우가 많습니다.
    • 하이퍼파라미터 튜닝 용이성: 학습률 감소 스케줄이 미리 정의된 함수를 따르므로, 수동으로 학습률을 조절하는 것보다 편리할 수 있습니다.

4.2, 4.3의 모델 결과에 대한 정량, 정성 평가는 생략

4.4 Ablation Study

• 입력 뷰 수 (Number of Views):
  • 단일 입력 뷰(1-view) 모델과 본 논문에서 사용하는 다중 입력 뷰(4-view) 모델을 비교했습니다.
  • Splatter image와 유사하게 단일 뷰만을 입력으로 사용하는 이미지-투-3D(image-to-3D) 모델을 훈련했습니다. 그러나 하나의 이미지만 input으로 받을 경우 가우시안이 너무 sparse 해지므로, 이 모델은 출력 특징 맵 하나의 픽셀 당 두 개의 3D Gaussian을 예측하여 총 128 x 128 x 2 = 32,768개의 Gaussian을 생성합니다.
  • 결과적으로 단일 뷰 모델은 정면 뷰(front-view)는 잘 재구성하지만, 후면 뷰(back-view)를 구별하지 못하고 흐릿하게(blurriness) 나타내는 한계를 보였습니다. 이는 회귀(regressive) 방식의 U-Net이 재구성 작업에 더 적합하며, 대규모 데이터셋에서는 일반화하기 어렵기 때문이라고 설명합니다.
• 데이터 증강 (Data Augmentation):
  • 모델 훈련 시 데이터 증강(data augmentation) 기법을 적용했을 때와 적용하지 않았을 때의 효과를 검증했습니다.
  • 훈련 데이터는 Objaverse 데이터셋에서 렌더링된 실제 이미지인 반면, 추론 시에는 MVDream, ImageDream과 같은 확산 모델(diffusion model)로 합성된 다중 뷰 이미지를 사용하므로 도메인 간의 차이(domain gap)가 발생합니다.
  • 이러한 도메인 간의 차이를 줄이기 위해 Grid Distortion과 Orbital Camera Jitter의 두 가지 데이터 증강 기법을 제안했습니다.
    • Grid Distortion: 첫 번째 입력 뷰를 제외한 나머지 세 개의 입력 뷰를 무작위 격자(random grid)로 왜곡시켜 다중 뷰 이미지 간의 미묘한 불일치를 시뮬레이션합니다. 이는 모델이 불일치하는 다중 뷰 입력 이미지에 더 강건하도록 만듭니다.
    • Orbital Camera Jitter: 카메라 포즈가 정확하지 않을 수 있는 문제에 대비하여 마지막 세 개의 입력 뷰에 대해 카메라 포즈에 임의의 회전(randomly rotate)을 적용합니다. 이를 통해 모델이 부정확한 카메라 포즈와 레이 임베딩(ray embeddings)에 더 강해지도록 합니다.
  • 데이터 증강을 적용하지 않은 모델은 훈련 손실(training loss)이 더 낮게 나타났지만, 추론 시에는 더 많은 플로터(floaters: 원치 않는 떠다니는 입자)와 나쁜 형상(worse geometry)을 생성하는 것을 확인했습니다. 데이터 증강 전략을 사용한 모델이 생성된 다중 뷰 이미지의 3D 불일치와 부정확한 카메라 포즈를 더 잘 보정함을 보여줍니다.
• 훈련 해상도 (Training Resolution):
  • 더 적은 수의 Gaussian과 더 작은 렌더링 해상도를 가진 모델을 훈련하여 해상도가 결과물에 미치는 영향을 분석했습니다.
  • U-Net의 마지막 업 블록(up block)을 제거하여 출력 Gaussian 수가 16,384개(64x64x4)가 되도록 하고, 256x256 해상도에서 렌더링하여 학습했습니다.
  • 이 모델은 3D Gaussian을 재구성할 수 있었지만, 256x256 입력 다중 뷰 이미지에 비해 디테일(details)이 떨어지는 결과를 보였습니다. 반면, 512x512의 더 높은 해상도 모델은 더 나은 디테일을 포착하고 고해상도 Gaussian을 생성할 수 있음을 입증했습니다.